Complexe simplicial - Définition

Homologie simpliciale

Considérons un Δ-complexe où A₀ est l'ensemble des sommets et A_n l'ensemble des n-faces.

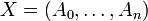
Pour chaque entier naturel n, on note Δ_n(X) le groupe abélien libre de base A_n. Les éléments de Δ_n(X) seront appelés les n-chaines. En d'autre termes, une n-chaine est une combinaisons linéaires à coefficients entiers de n-faces du complexe X.

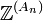
On définit le bord d'un simplexe de la façon suivante :

Par exemple :

• Le bord d'un segment est égal à son extrémité privé de son origine
• le bord d'un triangle est égal à la somme des trois côtés avec un signe moins tenant compte de l'orientation

• le bord d'un tétraèdre est donné par la formule

Par linéarité, le bord se prolonge en un morphisme de groupe δ_n de Δ_n(X) vers Δ_{n − 1}(X). On a et obtient ainsi un complexe de chaine . Les groupes d'homologie de l'espace X sont les .

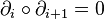
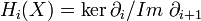
Même si ce n'est pas évident a priori, si deux Δ-complexes sont homéomorphes et plus généralement, s'ils ont le même type d'homotopie, alors leurs groupes d'homologie sont identiques.

Exemples

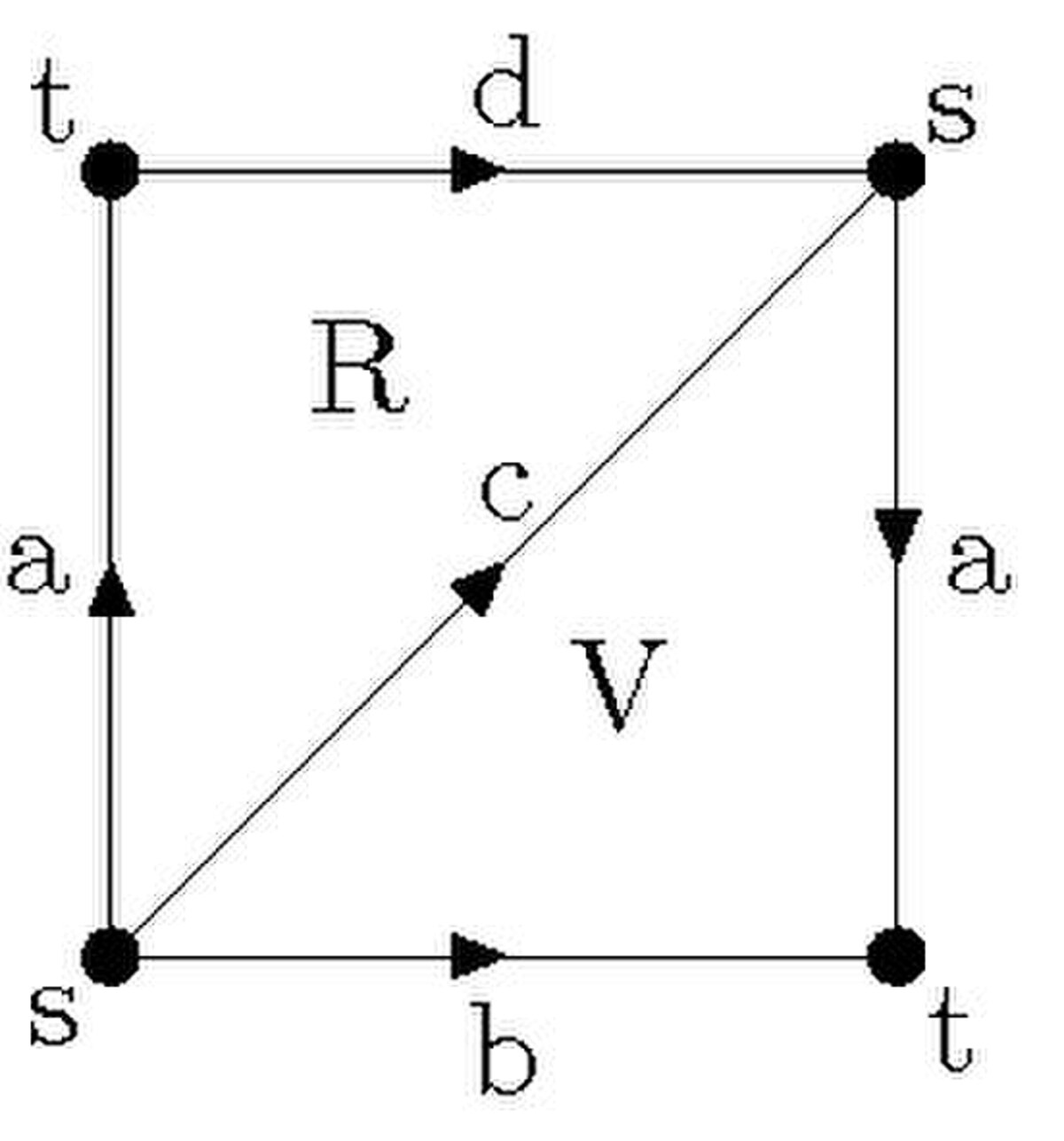
• Le tore - Il est possible de trianguler le tore avec un sommet s, trois arêtes a,b,c et deux faces R et V. On part de la représentation classique du tore par un carré dont on recolle les côtés opposés et on coupe ce carré en deux pour obtenir des triangles. On obtient ainsi une structure de Δ-complexe.
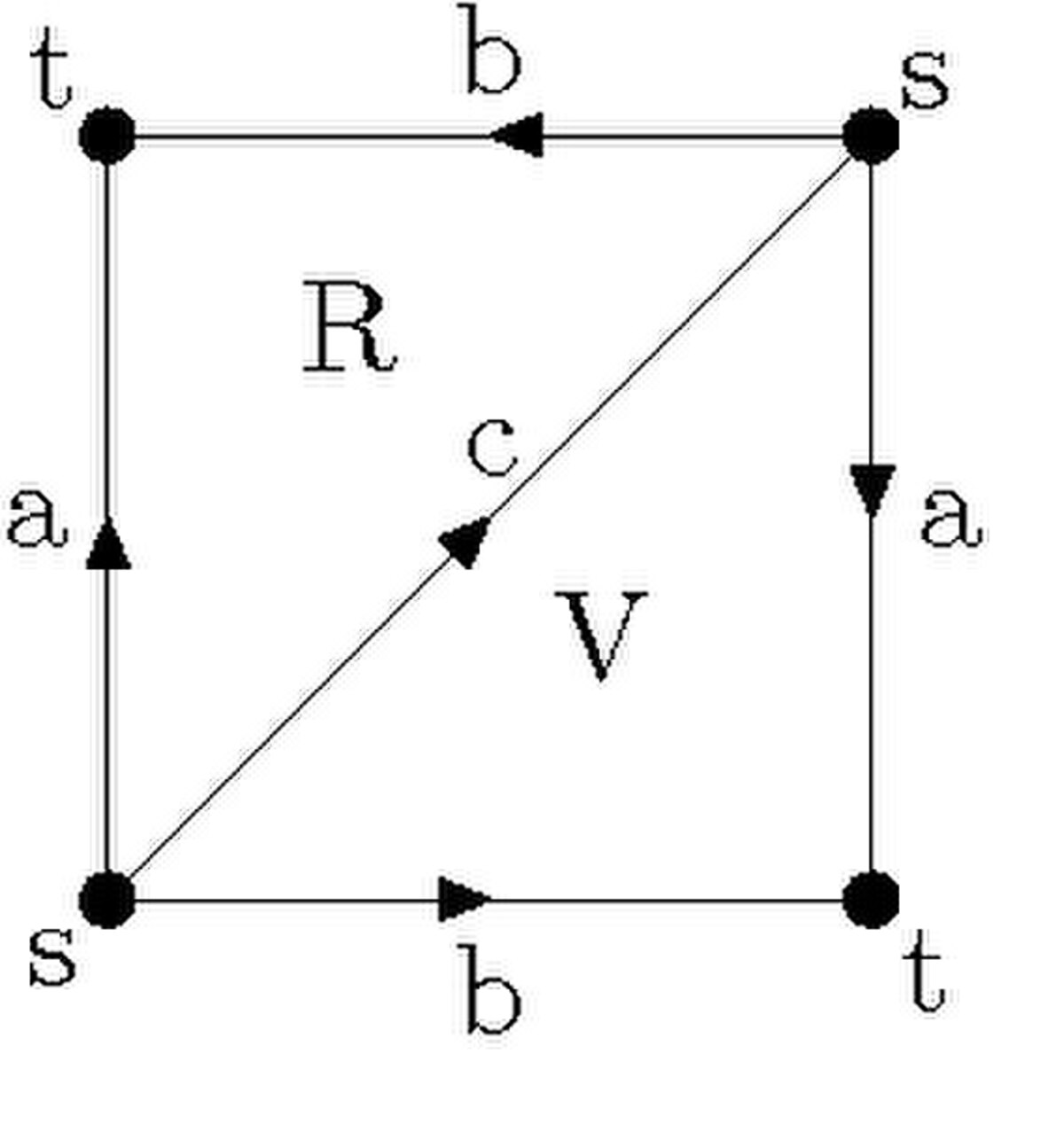
• Le ruban de Moebius - Le ruban de Moebius diffère du tore de deux manière. D'une part, on ne recolle qu'un bord du carré, le deuxième bord reste libre. D'autre part, on fait pivoter avant de recoller. D'où le diagramme ci-contre. Cette fois, on a deux sommets s et t, quatre arêtes a, b, c et d et toujours deux faces R et V.
• Le plan projectif - Le plan projectif plus difficile à visualiser vu qu'il ne se plonge pas dans l'espace usuel. On l'obtient en recollant les bord du ruban de Moebius suivant le diagramme. Il existe une autre façon de recoller qui elle donne une bouteille de Klein. (Dans ce cas il n'y aura qu'un seul sommet comme pour le tore.) Ici, on a deux sommets s et t, trois arêtes a, b, c et deux faces R et V.

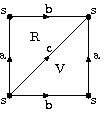
Le tore

Le ruban de Moebius

Le plan projectf

Résultats généraux.

• H₀(X) est un groupe abélien libre engendré par les composantes connexes de X.
• Si X a plusieurs composantes connexes .
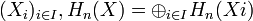
• Si X est connexe, H₁(X) est l'abélianisé du groupe fondamental π₁(X).
• En notant Sⁿ la sphère de dimension n, on a , et H_p(S_n) = 0 dans tous les autres cas.

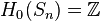
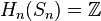
Calculs effectifs

On peut vérifier sur quelques exemples que le calcul des groupes d'homologie d'un espace triangulé par un Δ-complexe est un jeu d'enfants.

Homologie du tore

Dans le cas du tore T , , et . L'application est nulle (voir le schéma). D'autre part δ₂(R) = c − b − a et δ₂(V) = b + a − c.

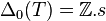
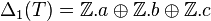
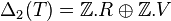
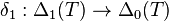
Vu que δ₁ = 0, on a . D'autre part et , ce qui donne et .

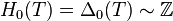
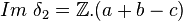
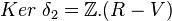
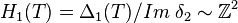
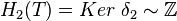
On peut interpréter les choses ainsi : signifie que T est connexe. signifie que T se referme sur lui-même dans deux directions différentes. signifie que T enferme un volume.

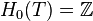
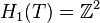
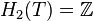
Homologie du ruban de Moebius

Dans le cas du ruban de Moebius, M , , et .

et donc .

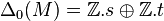
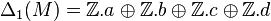
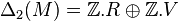
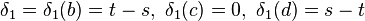
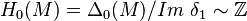
On a et . Finalement .

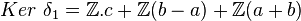
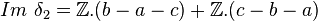
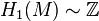
δ₂ est injective donc H₂(M) = 0.

Homologie du plan projectif

Dans le cas du plan projectif, M , , et .

et donc .

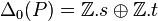
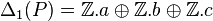
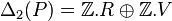
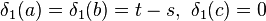
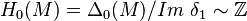
On a et . Finalement . il y a une petite finesse ici, c n'est pas dans mais 2c y est .

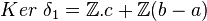
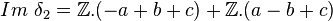
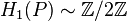
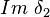
δ₂ est injective donc H₂(P) = 0.