Connexion de Ehresmann - Définition

Cas spéciaux

Fibrés principaux et connexions principales

Soit E un fibré G-principal sur M. Alors une connexion de Ehresmann H sur E est dite connexion de Ehresmann principale si elle est invariante l'action de G sur E au sens où : H_eg = d(R_g)_e(H_e) pour tout e∈E et g∈G; ici d(R_g)_e est la différentielle de l'action à droite de g sur E au point e.

Les sous-groupes à un paramètre de G agissent verticalement on E. La différentielle of cette action permet d'identifier le sous-espace V_e avec l'algèbre de Lie g du groupe G, par exemple par l'application . La forme de connexion v de la connexion de Ehresmann peut être interprétée comme une 1-forme ω sur E à valeurs dans g définie par ω(X)=ι(v(X)).

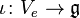
Ainsi réinterprété, la forme de connexion ω satisfait les deux propriétés suivantes :

• Elle se transforme de façon équivariante sous l'action du groupe G : pour tout h ∈G, où R_h^* est le pullback sous l'action à droite et Ad est la représentation adjointe de G sur son algèbre de Lie.
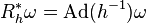
• Elle fait correspondre les champs de vecteurs verticaux à leur éléments associés dans l'algèbre de Lie: ω(X)=ι(X) pour tout X ∈V.

Inversement, on peut montrer qu'une telle 1-forme à valeur dans G sur un fibré principal engendre une distribution horizontale qui satisfait les propriété mentionnées ci-dessus.

A partir d'une trivialisation locale, on peut réduire ω aux champs de vecteur horizontaux dans cette trivialisation. Cela définie une 1-form ω' sur B via le pullback. La forme ω' détermine ω complètement mais de façon dépendante de la trivialisation. (Souvent, cette forme est aussi appelée une forme de connexion et notée simplement ω.)

Fibré vectoriel et dérivées covariantes

Soit E un fibré vectoriel régulier sur M. Une connexion de Ehresmann H sur E est dite connexion linéaire de Ehresmann si H_e dépend linéairement de e ∈ E_x pour chaque x ∈ M. Plus précisément, soit S_λ la multiplication scalaire par λ sur E, et soit l'addition. Alors H est linéaire si et seulement si pour tout x ∈ M, les propriétés suivantes sont satisfaites :

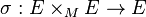
• H_λe = d(S_λ)_e(H_e)pour tout e ∈ E et tout scalaire λ.
• où est le sous-fibré horizontal sur .

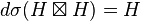
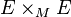
Puisque E est un fibré vectoriel, son fibré vertical V est isomorphe à π*E. Et donc, si if s est une section de of E, alors v(ds):TM→s*V=s*π*E=E. Le fait que la connexion de Ehresmann est linéaire implique que c'est un homomorphisme de fibré vectoriel, et il est donc donné par une section ∇s du fibré vectoriel Hom(TM,E), appelé la dérivée covariante de s.

Réciproquement, une dérivée covariante ∇ sur un fibré vectoriel définit une connexion de Ehresmann linéaire par H_e, pour e ∈ E avec x=π(e), comme étant l'image ds_x(TM) où s est une section de E telle que ∇s_x=0.

Remarquons que pour des raisons historiques, le terme "linéaire" ( ou le terme "affine" — cf. Connexion affine ), quand il est appliqué à des connexions, est parfois utilisé pour désigner des connexions sur le fibré tangent ou un fibré principal.

Fibrés associés

Une connexion de Ehresmann sur un fibré muni d'une structure de groupe peut parfois engendrer une connexion de Ehresmann sur un fibré associé. Par exemple, une connexion linéaire dans un fibré vectoriel E, en munissant E de la notion de "parallélisme" comme indiqué ci-dessus, induit une connexion sur le fibré principal PE des repères tangents à E. Inversement, une connexion dans PE induit une connexion linéaire dans E pourvu que la connexion dans PE soit équivariante sous l'action du groupe linéaire de transformation des repères de l'espace tangent (et ainsi elle est une connexion principale). Il n'est pas toujours possible qu'une connexion de Ehresmann induise, de façon naturelle, une connexion sur un fibré associé, en particulier dans le cas où elle n'est pas équivariante.

Supposons que E est un fibré associé à P, de telle sorte que E = P ×_G F. Une G-connexion sur E est une connexion de Ehresmann telle que l'application de transport parallèle τ : F_x → F_x′ est donnée par une G-transformation des fibres (pour des points x et x′ de "M" suffisamment proche et joint par une courbe).

Pour une connexion principale sur P, on obtient une G-connexion sur le fibré associé E = P ×_G F via le pullback.

Inversement, à partir d'une G-connexion sur E donnée, il est possible de retrouver la connexion principale sur le fibré principal "P" associé. Pour retrouver cette connexion principale, on introduit la notion de repère sur la fibre type "F". Puisque G est un groupe de Lie de dimension finie qui agit effectivement sur F, il existe une configuration finie de points (y₁,...,y_m) dans F tels que la G-orbite R = {(gy₁,...,gy_m) | g ∈ G} soit un espace homogène principal de G. On peut voir R comme étant une généralisation de la notion de repère pour une action de "G" sur F. Remarquons que puisque R est un espace homogène principal oiur G, le fibré E(R) associé à E avec la fibre type R est équivalent au fibré principal associé à E. Mais c'est aussi un sous-fibré du m-produit de fibré de E avec lui-même. La distribution des espaces horizontaux sur E induit une distribution d'espace sur ce fibré produit. Puisque les applications du transport parallèle associées à la connexion sont des G-applications, elles préservent le sous-espace E(R), et ainsi la G-connexion s'abaisse en une G-principale sur E(R).

En résumé, il y a une correspondance bijective (à une équivalence près) entre les connexions abaissées des connexions principales sur les fibrés associés, et les G-connexions sur les fibrés associés. Pour cette raison, dans la catégorie des fibrés avec une structure de groupe G, la connexion principale contient toutes les informations concernant les G-connexions sur les fibrés associés. En conséquence, on travaille habituellement directement avec la connexion principale, à moins qu'il n'y ait une raison majeure pour prendre en considération les connexions sur les fibrés associés ( comme c'est le cas, par exemple, pour les connexions de Cartan).