Connexion de Ehresmann - Définition

Propriétés

Courbure

Soit v une connexion de Ehresmann. Alors la courbure de v est donnée par

où [-,-] est le crochet de Frölicher-Nijenhuis v ∈ Ω¹(E,TE) avec lui-même. Ainsi R ∈ Ω²(E,TE) est la forme différentielle de degré 2(ou 2-forme) sur E à valeurs dans TE définie par : , ou, en d'autres termes : R(X,Y) = [X_H,Y_H]_V, où X = X_H + X_V est la décomposition en somme directe dont les composantes sont respectivement dans H et V. De cette dernière expression de la courbure, nous voyons qu'elle est identiquement nulle si et seulement si le sous-fibré horizontal est intégrable au sens de Frobenius. Ainsi la courbure mesure la condition d'intégrabilité pour que sous-fibré horizontal donne des sections transversales du fibré E → M.

La courbure d'une connexion de Ehresmann satisfait aussi une version de l'identité de Bianchi:

[v,R] = 0

où encore une fois [-,-] désigne le crochet de Frölicher-Nijenhuis de ∈ Ω¹(E,TE) et R ∈ Ω²(E,TE).

Complétude

Une connexion de Ehresmann permet aux courbes d'avoir localement un unique relèvement horizontal. Une connexion de Ehresmann est dite complète si les courbes peuvent être relevées horizontalement sur l'ensemble de leur domaine de définition.

Holonomie

Le fait qu'une connexion soit plate correspond localement à l'intégrabilité au sens de Frobénius des espaces horizontaux. A l'opposé, une courbure qui ne s'annule pas, implique la présence d'une holonomie (en) de la connexion.

Définition formelle

Soit p: E → M un fibré Soit V = ker (dp : TE → p*TM) le fibré vertical constitué des vecteurs tangents aux fibres E, de telle sorte que la fibre de V en e∈E est T_e(E_p(e)).

Définition via les sous-espaces horizontaux

Une Connexion de Ehresmann sur E est un sous-fibré régulier H de TE, appelé le fibré horizontal de la connexion, qui est un complémentaire de V, dans le sens où il définit une décomposition en somme directe : TE = H⊕V ().

De façon plus détaillée, le fibré horizontal a les propriétés suivantes :

• Pour chaque point e ∈ E, H_e est un sous-espace vectoriel de l'espace tangent T_eE à E en e, appelé le "sous-espace horizontal" de la connexion en e.
• H_e dépend régulièrement de e.
• Pour chaque e ∈ E, H_e n V_e = {0}.
• Chaque vecteur tangent de T_eE (pour chaque e∈E) est la somme d'une composante horizontale et d'une composante verticale, de telle sorte que T_eE = H_e + V_e.

En termes plus sophistiqués, une telle donnée d'espaces horizontaux satisfaisant ces propriétés correspond précisément à la section régulière d'un fibré des jets de différentielles J¹E →E.

Définition via une forme de connexion

De façon équivalente, soit v la projection sur le fibré vertical V selon H (de telle sorte que H = ker v). Elle est déterminée par la décomposition en "somme directe" de TE en ses parties verticale et horizontale mentionnée ci-dessus. Elle est parfois appelée la forme de connexion de la connexion de Ehresmann. Ainsi v est un homomorphisme de fibré vectoriel de TE dans lui-même avec les propriétés suivantes :

• v² = v;
• L'image de v est V.

Inversement, si v est un endomorphisme de fibré vectoriel de TE satisfaisant ces deux propriétés, alors H = ker v est le sous fibré horizontal d'une connexion de Ehresmann.

Transport parallèle par relèvement horizontaux

Une connexion de Ehresmann prescrit aussi une manière de relever des courbes depuis la variété de base M jusque dans l'espace total du fibré E de telle sorte que les tangentes aux courbes soient horizontales. Ces relèvements horizontaux sont un analogue direct du transport parallèle pour d'autres versions du formalisme des connexions.

De façon spécifique, supposons que γ(t) est une courbe régulière de M passant par le point x = γ(0). Soit e∈ E_x un point de la fibre sur x. Un relèvement de γ passant par e est une courbe de l'espace total E telle que : , et Un relèvement est horizontal si, de plus, chaque tangente de la courbe est contenue dans le sous-fibré horizontal de TE :

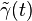
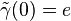
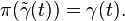
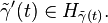
On peut montrer en utilisant le théorème du rang appliqué à π et v que chaque vecteur X∈T_xM a un unique relèvement en un vecteur . En particulier, le champ tangent à γ engendre un champ de vecteur horizontal dans l'espace total du fibré induit γ*E. Selon le théorème de Cauchy-Lipschitz, ce champ de vecteur est intégrable. Ainsi, pour chaque courbe γ et chaque point e sur x=γ(0), il existe un unique relèvement horizontal de γ passant par e pour un temps t suffisamment petit.

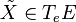
Remarquons que, dans le cas général, le relèvement horizontal d'une connexion de Ehresmann, est dépendant du chemin. Quand deux courbes régulières de M, qui coïncident en γ₁(0) = γ₂(0) = x₀ et qui se coupent aussi en un autre point x₁∈M, sont relevée horizontalement dans E de telle sorte qu'elle passent par le même point e∈π^-1(x₀), elle passerons en général par des points différents de π^-1(x₁). Ceci a une conséquence importante pour la géométrie différentielle des fibrés : l'espace des sections de H n'est pas une sous-algèbre de Lie de l'espace des champs de vecteurs sur E, parce que, en général, il n'est pas fermé pour le crochet de Lie de champs de vecteurs. La courbure de la connexion mesure ce défaut de fermeture sous l'action du crochet de Lie.