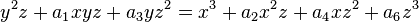Courbe elliptique - Définition
La liste des auteurs de cet article est disponible ici.
Multiplication complexe
L'addition permet naturellement de définir la multiplication d'un point de la courbe par un nombre entier (par exemple (-3). P est défini par -(P+P+P)). Mais il peut arriver que la courbe ait d'autres multiplications. Par exemple, sur la courbe d'équation affine y2 = x3 − x, définie sur le corps des rationnels, on peut aussi définir une multiplication par i (le nombre complexe tel que i2 = − 1), en posant i.P(x,y) = P'( − x,iy), et plus généralement on peut définir la multiplication des points par n'importe quel entier de Gauss, c'est-à-dire n'importe quel nombre complexe de la forme a + bi, avec a,b des entiers relatifs.
Pour des courbes elliptiques définies sur des corps de caractéristique 0 (par exemple le corps des rationnels), ce sont essentiellement les deux seuls cas possibles : soit il n'y a que la multiplication par des entiers relatifs, soit il y a multiplication complexe par un ordre dans un corps quadratique imaginaire.
Courbes elliptiques sur les corps finis
Soit
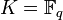
Théorème —
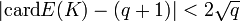
Autrement dit, l'ordre de grandeur du nombre de points de la courbe est à peu près le même que le nombre d'éléments dans le corps.
L'ensemble des points
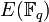
Par exemple la courbe d'équation y2 = x3 − x définie sur
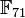
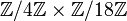
L'étude de cette courbe sur des extensions de
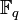
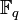
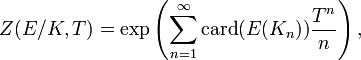
où les corps Kn sont les extensions de
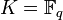
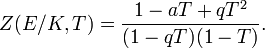
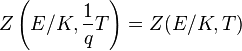
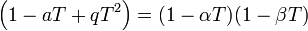

Ces résultats constituent les conjectures de Weil pour les courbes elliptiques. Par exemple, la fonction zêta de y2 + y = x3 sur le corps
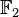
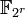
Les courbes elliptiques définies sur des corps finis ont des applications en algorithmique, notamment en cryptographie et pour la factorisation d'entiers. Généralement, l'idée derrière la composition originale de ces algorithmes fut celle d'une généralisation des corps finis, plus précisément du groupe multiplicatif
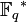
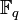
Repères chronologiques
Quelques précisions sur le point à l'infini et les équations
Point à l'infini
Le cadre usuel pour définir et décrire les courbes elliptiques est celui de l'espace projectif sur un corps K. En dimension 2, dans le plan projectif, les points sont donnés par trois coordonnées x, y, z, en excluant le triplet (0, 0, 0) et en identifiant les points de coordonnées (x, y, z) et (λx, λy, λz), pour tout nombre λ non nul dans le corps K. Lorsque z est différent de 0, disons, on peut représenter le point (x, y, z) par (x / z, y / z, 1), et donc lui associer un point du plan affine usuel (x / z, y / z). Les points pour lesquels z est égal à 0 forment une droite 'à l'infini'.
Dans ce cadre, une courbe elliptique sur le corps K est définie par une équation cubique homogène:
où les coefficients a1, a2, a3, a4, a6 appartiennent à K donné et sous la condition que la courbe ainsi définie ne soit pas singulière. Cette dernière condition s'exprime par le fait qu'un certain polynôme en les coefficients (analogue au Δ donné plus haut) ne s'annule pas.
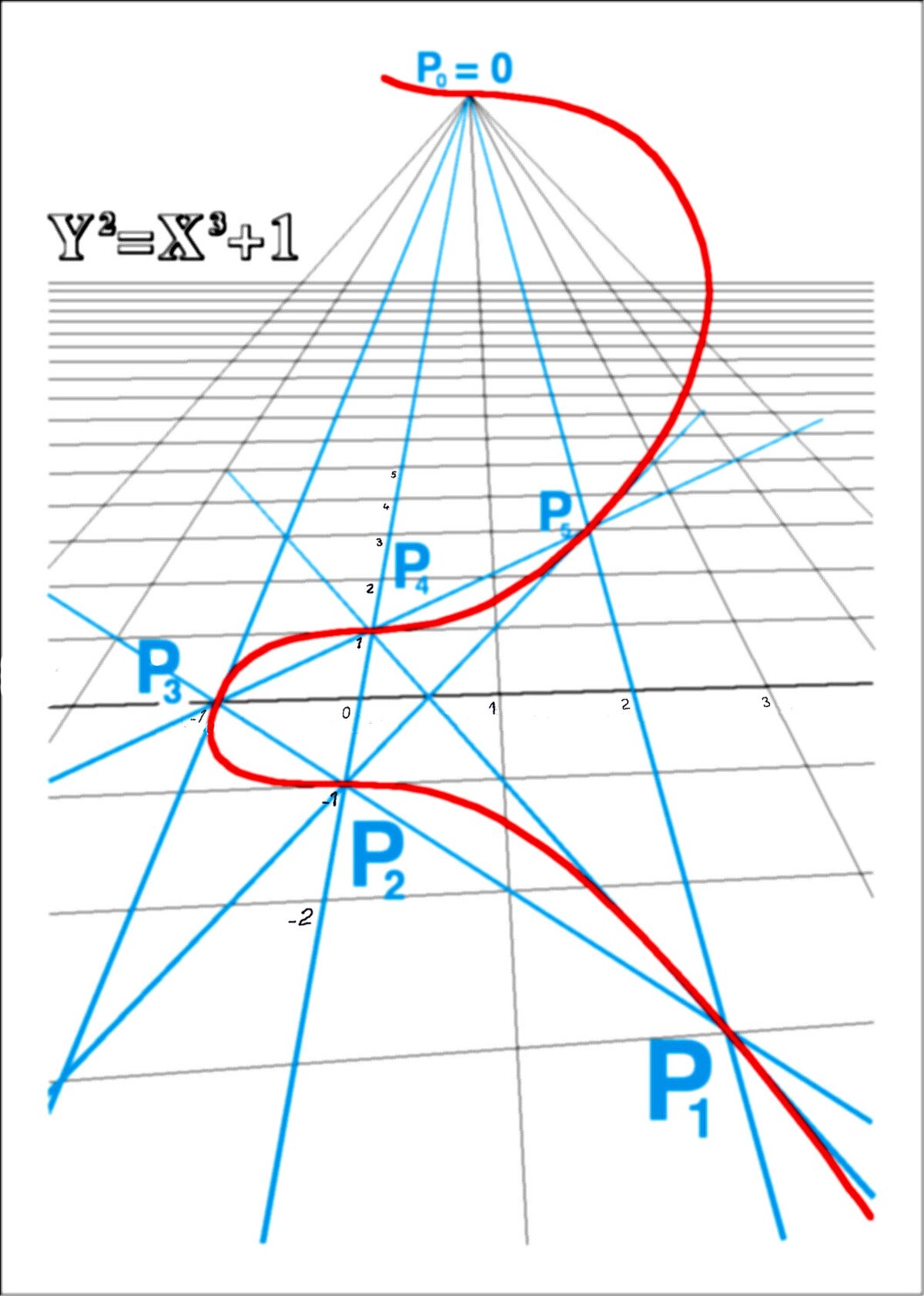
Que se passe-t-il à l'infini, c'est-à-dire pour z = 0 ? On trouve que x = 0, donc y ne peut être nul et le seul point de la courbe à l'infini est le point (0, 1, 0) (rappelons que dans le plan projectif, (0, y, 0) et (0, 1, 0) définissent le même point). Pour z distinct de 0, on peut diviser toutes les coordonnées par z3 et l'équation devient celle dans le plan affine donnée au début de l'article.
Le point à l'infini (qui est un point d'inflexion) est mis en valeur sur la représentation ci-contre de la courbe dont l'équation affine est y2 = x3 + 1 .