Courbe elliptique - Définition
La liste des auteurs de cet article est disponible ici.
Courbes elliptiques sur le corps des nombres rationnels
Une courbe E définie sur le corps des nombres rationnels est aussi définie sur le corps des réels, donc la construction d'une addition sur les points (à coordonnées réelles) par la méthode des tangentes et des sécantes s'applique ici. Il est facile de voir que si deux points ont des coordonnées rationnelles, la droite qui les joint a une équation à coefficients rationnels et le 3e point d'intersection avec la courbe est encore à coordonnées rationnelles. Il en est de même pour le symétrique par rapport à l'axe des abscisses d'un point à coordonnées rationnelles. Finalement, on montre que le groupe E(Q) des points de la courbe à coordonnées rationnelles forme aussi un groupe abélien.
La structure du groupe des points rationnels
Le résultat le plus important est que tous les points à coordonnées rationnelles peuvent être construits par la méthode de la tangente et de la sécante à partir d'un nombre fini d'entre eux. Plus précisément:
Théorème de Mordell-Weil — Le groupe
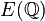
Il est donc la somme directe d'un nombre fini de copies de
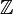
La démonstration requiert deux ingrédients : d'abord, on montre que pour tout entier m > 1 (par exemple m = 2), le groupe-quotient
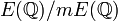
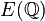
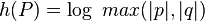
La preuve du théorème est alors une variante de la méthode de descente infinie et repose sur l'application successive de 'divisions euclidiennes' sur la courbe : soit
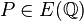
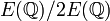
Le théorème de Mordell-Weil n'est pas pour l'instant effectif, car on ne connaît pas de procédure générale pour déterminer les représentants de
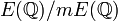
Le nombre de copies de
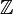
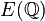
de rang 18, trouvée par Noah Elkies en 2006 (des courbes de rang supérieur à 28 sont connues, mais on ne sait pas encore en déterminer exactement le rang).
Quant aux groupes cycliques qui forment donc le sous-groupe de torsion des points à coordonnées rationnelles de E, les possibilités sont les suivantes:
Théorème de Mazur — Le sous-groupe de torsion de
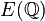
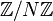
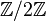
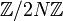
On connaît des exemples pour toutes ces possibilités. De plus, les courbes avec le même groupe de torsion appartiennent à une famille à un paramètre.
Exemples
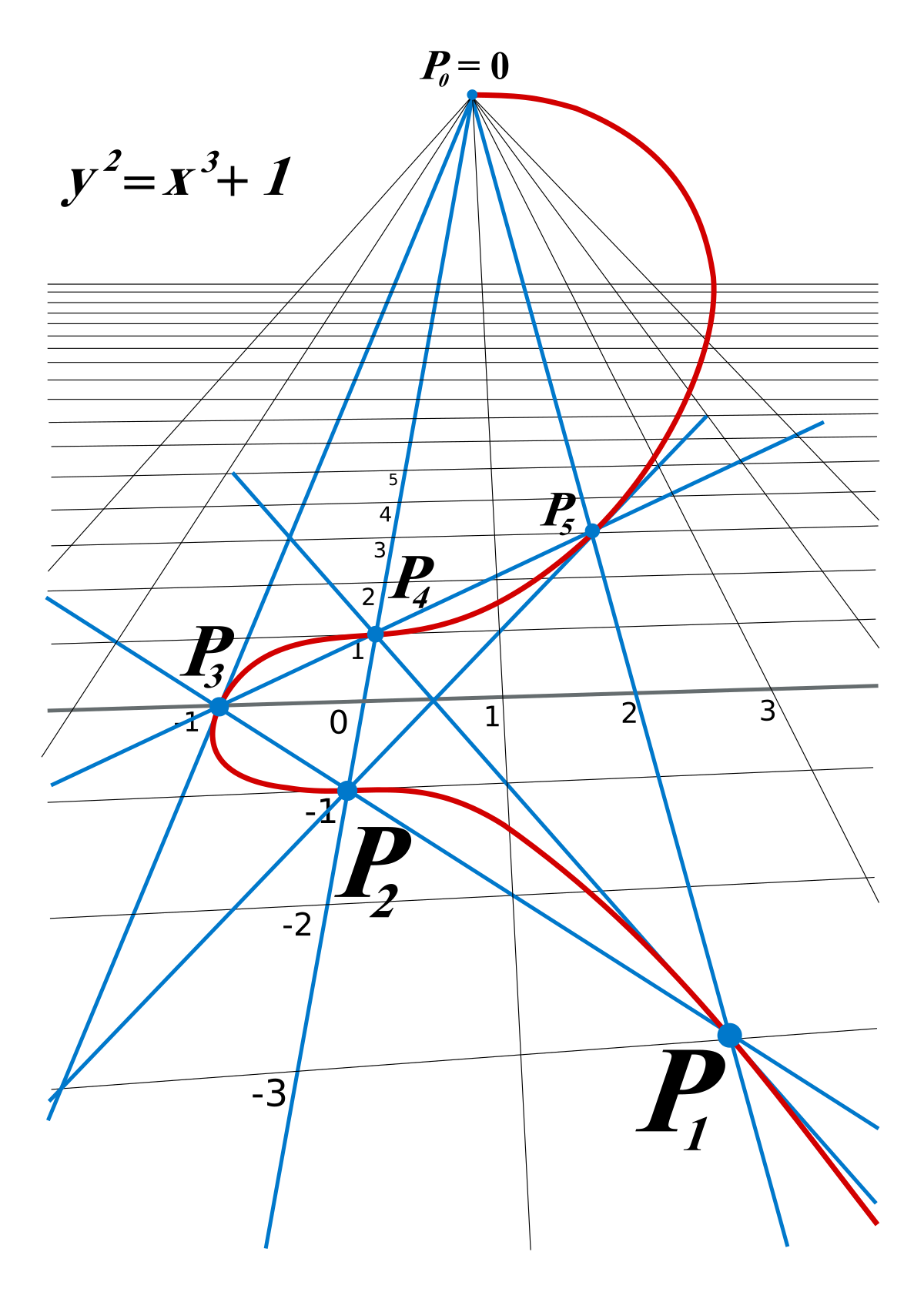
- La courbe d'équation y2 = x3 + 1
Le rang de cette courbe est nul et elle a 6 points à coordonnées rationnelles : outre le point à l'infini, les points de coordonnées (2,3), (0, 1), (-1,0 ), (0, -1), (2, -3). On peut prouver que ce groupe est cyclique d'ordre 6 et qu'il est engendré par le point (2, 3). On a ainsi : (0, 1) = 2 (2, 3) (dans le sens de (2, 3)+(2, 3) pour la loi d'addition sur la courbe), (-1, 0 )= 3 (2, 3), (0, -1) = -2(2,3)= 4 (2, 3) et (2, -3)=-(2, 3)= 5(2, 3) ; le point à l'infini est égal à 6 (2, 3).
Ces relations se voient sur le graphe réel de la courbe. Par exemple, la tangente à la courbe au point de coordonnées (2, 3) passe par le point (0, -1) dont le symétrique est (0, 1), donc (0, 1) = 2 (2, 3). Les points de coordonnées (-1, 0), (0, -1) et (2, -3) sont alignés, donc la somme des deux premiers est égale au point (2, 3).
Considérée comme courbe sur le corps des nombres complexes, cette courbe est associée au réseau L de périodes
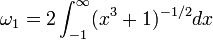
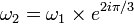
- La courbe d'équation y2 = x3 + 109858299531561
Le rang de cette courbe est 5 et elle a de plus trois points de torsion à coordonnées rationnelles, formant un groupe cyclique d'ordre 3. Son groupe de Mordell-Weil
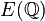
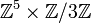
Voici une liste de 5 points générateurs indépendants d'ordre infini (engendrant donc les 5 copies de
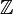
(735 532, 630 902 573), (49704, 15 252 915), (-4578, 10 476 753), (-15260, 10 310 419), (197 379, 88 314 450).
Les trois points de torsion à coordonnées rationnelles sont le point à l'infini, le point (0, 10 481 331), d'ordre 3, et son opposé.
Tous les points à coordonnées rationnelles de cette courbe s'obtiennent alors par combinaison linéaire à coefficients entiers des 6 points explicités.
- La courbe d'équation y2 = x3 − 36x
Son groupe de Mordell-Weil est isomorphe à
Dans les Arithmétiques de Diophante, le problème V. 8 demande de construire trois triangles de même aire. L'Observation 23 de Pierre de Fermat, qui commente ce problème, affirme que pour un triangle donné quelconque, il "en fourni[t] une infinité ayant la même aire" et pour l'aire 6, donne, en plus de la solution évidente du triangle de côtés 3, 4, 5, celui de côtés 7/10, 120/7, 1201/70, et celui de côtés 2 896 804/1 319 901, 7 216 803/1 319 901, 7 776 485/1 319 901. À partir du point P = (2,1) sur la courbe 6y2 = x3 − x (ou (12, 36) sur la courbe y2 = x3 − 36x), point qui correspond au triangle de côtés 3, 4, 5, le point
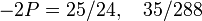
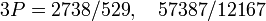
Le lien entre recherche des aires de triangles rectangles en nombres (ce qu'on appelle des 'nombres congruents') et courbes elliptiques a été exploré plus systématiquement par J. Tunnell en 1983.
La conjecture de Birch et Swinnerton-Dyer
La conjecture de Birch et Swinnerton-Dyer est l'un des problèmes du millénaire pour la solution desquels la fondation Clay a promis un million de dollars. Dans le cas des courbes elliptiques, cette conjecture relie des objets analytiques et arithmétiques définis à partir de la courbe considérée.
Du côté analytique, un ingrédient important est la fonction d'une variable complexe, L de Hasse-Weil de la courbe E sur
Si y2 + a1y + a3 = x3 + a2x2 + a4x + a6 est une équation minimale de la courbe elliptique E sur
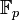
La fonction zêta d'une courbe elliptique sur un corps fini est en quelque sorte une fonction génératrice rassemblant les informations sur le nombre de points de la courbe dans toutes les extensions (finies) du corps de base. Plus précisément,

La somme à l'intérieur de l'exponentielle ressemble au développement d'un logarithme et, de fait, la fonction Z ainsi définie est une fonction rationnelle :
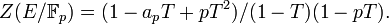
La fonction de Hasse-Weil de la courbe elliptique sur
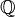
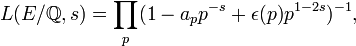
où ε(p) = 1 si la courbe a bonne réduction en p et 0 sinon (dans ces derniers cas, en nombre fini, le terme ap doit aussi être défini).
Ce produit converge seulement pour  . Mais la conjecture de Hasse prédisait que la fonction L admet un prolongement analytique à tout le plan complexe et vérifie une équation fonctionnelle liant, pour tout s, sa valeur en s à sa valeur en 2-s. La conjecture de Hasse est maintenant (depuis 1999) démontrée comme conséquence de la preuve de la conjecture de Shimura-Taniyama-Weil : cette dernière affirme en effet que toute courbe elliptique définie sur
. Mais la conjecture de Hasse prédisait que la fonction L admet un prolongement analytique à tout le plan complexe et vérifie une équation fonctionnelle liant, pour tout s, sa valeur en s à sa valeur en 2-s. La conjecture de Hasse est maintenant (depuis 1999) démontrée comme conséquence de la preuve de la conjecture de Shimura-Taniyama-Weil : cette dernière affirme en effet que toute courbe elliptique définie sur
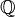
On peut donc parler des valeurs de la fonction L de Hasse-Weil en tout point du plan complexe. La conjecture de Birch et Swinnerton-Dyer lie le comportement au centre de la bande critique (en s=1, donc) à l'arithmétique de la courbe. Elle prévoit en particulier :
Conjecture - L'ordre du zéro de la fonction L de la courbe elliptique E au voisinage de s=1 est égal au rang de E.
Sous sa forme la plus précise, la conjecture prédit aussi la valeur du terme dominant au voisinage de 1, en fonction de diverses quantités liées à la courbe elliptique.
De même que l'hypothèse de Riemann, la conjecture de Birch et Swinnerton-Dyer a de multiples conséquences. En voici deux :
Théorème — Soit n un entier impair sans facteurs carrés. Supposons que la conjecture de Birch et Swinnerton-Dyer soit vraie. Alors, le nombre entier n est l'aire d'un triangle rectangle à côtés rationnels si et seulement si le nombre des triplets d'entiers (x,y,z) satisfaisant 2x2 + y2 + 8z2 = n est égal à deux fois le nombre des triplets satisfaisant 2x2 + y2 + 32z2 = n.
Cet énoncé, dû à Tunnell est lié au fait que n est l'aire d'un triangle rectangle en nombres rationnels si et seulement si la courbe elliptique y2 = x3 − n2x a un point rationnel d'ordre infini (donc, sous la conjecture de Birch et Swinnerton-Dyer, sa fonction L s'annule en 1). L'intérêt de l'énoncé est que la condition indiquée se vérifie facilement.
Dans un tout autre ordre d'idées, certaines méthodes analytiques permettent d'estimer l'ordre d'annulation au centre de la borne critique de familles de fonctions L. Si on admet la conjecture de Birch et Swinnerton-Dyer, ces estimations se transposent en informations sur le rang des familles de courbes elliptiques correspondantes. Par exemple :
Théorème — En admettant l'hypothèse de Riemann généralisée et la conjecture de Birch et Swinnerton-Dyer, le rang moyen des courbes elliptiques d'équation y2 = x3 + ax + b est inférieur à 2.
La conjecture de Taniyama-Shimura-Weil et son application au Théorème de Fermat
La Conjecture de Taniyama-Shimura-Weil, encore connue sous le nom de "conjecture modulaire", affirme que toute courbe elliptique sur
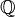
Autrement dit, si, pour  , on écrit la fonction L sous la forme
, on écrit la fonction L sous la forme

l'expression
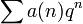
Par exemple, à la courbe elliptique y2 + y = x3 − x, de discriminant (et de conducteur) 37, est associée la forme f(z) = q − 2q2 − 3q3 + 2q4 − 2q5 + 6q6 + ..., avec q = exp(2πiz). Pour les nombres premiers l distincts de 37, on peut vérifier la propriété sur les coefficients. Ainsi pour l=3, les solutions de l'équation modulo 3 sont (0, 0), (0, 1), (0, 2), (1, 0), (1, 1), (1, 2), et on a donc bien a(3) = 3 − 6 = − 3.
La conjecture qui date du milieu des années 1950 a été finalement démontrée complètement en 1999, à partir des idées de Andrew Wiles, qui l'avait déjà prouvée en 1994 pour une large famille de courbes elliptiques.
Il existe plusieurs formulations de cette conjecture ; prouver leur équivalence n'était pas facile et a fait l'objet de travaux importants dans la seconde moitié du 20e siècle. Ainsi, la modularité d'une courbe elliptique E de conducteur N s'exprime aussi par le fait qu'il existe une application rationnelle non constante, défini sur
Par exemple, un paramétrage modulaire de la courbe elliptique y2 + y = x3 − x est donné par
avec comme toujours q = exp(2πiz). Les fonctions x(z) et y(z) sont ici modulaires de poids 0 et de niveau 37 ; autrement dit, elles sont méromorphes, définies sur le demi-plan supérieur  et telles que x(az + b / cz + d) = x(z) (et de même pour y(z)) pour tous les entiers a,b,c,d, avec ad − bc = 1 et 37 | c.
et telles que x(az + b / cz + d) = x(z) (et de même pour y(z)) pour tous les entiers a,b,c,d, avec ad − bc = 1 et 37 | c.
Une autre formulation repose sur la comparaison de représentations galoisiennes attachées d'une part aux courbes elliptiques, d'autre part à des formes modulaires, c'est cette dernière formulation qui a été utilisée dans la preuve de la conjecture. La gestion précise du niveau des formes (et leur lien au conducteur de la courbe) est particulièrement délicate.
L'application la plus spectaculaire de la conjecture est la preuve du Grand Théorème de Fermat. On suppose que, pour un nombre premier p>5, l'équation de Fermat ap + bp = cp ait une solution en entiers non nuls (donc qu'on ait trouvé un contre-exemple au Grand Théorème de Fermat). Alors la courbe elliptique y2 = x(x − ap)(x + bp), de discriminant Δ = (abc)2p / 256 ne peut être modulaire. Autrement dit, la preuve de la conjecture de Tanyama-Shimura-Weil pour cette famille de courbes elliptiques (appelées courbes de Hellegouarch-Frey) entraîne le Grand Théorème de Fermat. La preuve de ce lien entre les deux énoncés, sur une idée de G. Frey de 1985, est difficile et technique, elle n'a été établie par Kenneth Ribet qu'en 1987.
Points entiers
On s'intéresse ici aux points P = (x,y) de la courbe E tels que x soit entier. Le théorème suivant est dû à Siegel:
Théorème — L'ensemble des points P = (x,y) de E(Q) tels que x soit entier est fini.
Ce théorème s'étend d'ailleurs aux points dont la coordonnée x a un dénominateur divisible seulement par des nombres premiers appartenant à un ensemble fini, fixé à l'avance.
Il existe des formes effectives de ce théorème. Par exemple, si l'équation de Weierstrass de la courbe a des coefficients entiers plus petits qu'une constante H, les coordonnées (x,y) d'un point de la courbe telles que x et y soient entiers vérifient
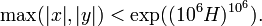
Exemple : L'équation y2 = x3 + 17 a huit solutions entières avec y>0 :
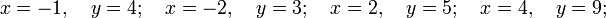
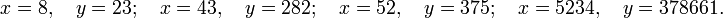
Généralisation aux corps de nombres
Une grande partie des résultats précédents est encore valable lorsque le corps de définition de la courbe elliptique est un corps de nombres, autrement dit une extension de degré fini du corps des nombres rationnels. En particulier,
Théorème de Mordell-Weil — Le groupe E(K) des points d'une courbe elliptique E définie sur un corps de nombres K à coordonnées dans K est de type fini.
Un théorème dû à Loïc Merel montre que pour un entier d donné, il n'existe qu'un nombre fini (à isomorphisme près) de groupes qui peuvent être la partie de torsion du groupe de Mordell-Weil E(K) d'une courbe elliptique E définie sur un corps de nombres K de degré d. Plus précisément
Théorème — Soit un entier d. Il existe un nombre B(d) tel que pour toute courbe elliptique E définie sur un corps de nombres K de degré d, tout point de torsion de E(K) a un ordre inférieur à B(d).
Le théorème est effectif, par exemple, pour d> 1, Merel montre que si un point de torsion est d'ordre p, p étant un nombre premier, on doit avoir
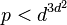
En ce qui concerne les points entiers, on a de même :
Théorème de Siegel — Soit une courbe elliptique E définie sur un corps de nombres K, x et y les coordonnées de Weierstrass, alors l'ensemble des points de E(K) dont la coordonnée x est dans l'anneau des entiers de K est fini.
Les propriétés de la fonction L de Hasse-Weil et la conjecture de Birch et Swinnerton-Dyer s'étendent également aux corps de nombres.