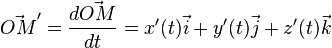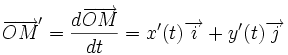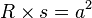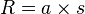Courbe - Définition

Définition des courbes gauches

On se place cette fois dans l'espace à trois dimensions usuel, muni d'un repère orthonormé .

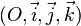
Équation paramétrique

L'équation paramétrique prend cette fois la forme

.

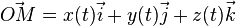
Le principe du calcul de la tangente est le même : en un point où le vecteur dérivé

est non nul, il y a une tangente à la courbe, dirigée par ce vecteur.

Équations cartésiennes

Une équation de la forme F(x,y,z)=C définit un ensemble appelé surface de niveau de la fonction F. Sous certaines conditions, l'intersection de deux surfaces de niveau définit une courbe et permet le calcul de sa tangente.

Voici le détail de ces conditions pour l'intersection

.

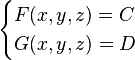
Si les fonctions F et G sont différentiables et que les vecteurs gradients de F et G en un point M de l'intersection sont des vecteurs indépendants, alors la courbe d'intersection possède une tangente dirigée par le vecteur

.

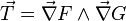
Avec les coniques, on a un exemple très classique d'introduction des courbes par intersection de surfaces : ce sont les courbes obtenues par intersection d'un cône de révolution et d'un plan.

Équation intrinsèque

Le principe est le mêmeq que pour les courbes planes, mais l'invariant de torsion peut intervenir. Par exemple, R le rayon de courbure et T le rayon de torsion, R = a et T = b (a, b donnés) déterminent une hélice circulaire.

Modes de définition d'une courbe plane

Il existe pour les courbes planes plusieurs modes d'introduction traditionnels. On se place ici dans le plan de la géométrie, muni d'un repère orthonormé . On fait l'hypothèse générale que les fonctions qui apparaissent sont dérivables. La raison de cette limitation apparaîtra un peu plus bas.

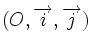
Équation paramétrique

Une courbe définie par une équation paramétrique est le lieu des points M(x,y), où x et y sont des fonctions d'un paramètre t prenant ses valeurs dans une partie de

.

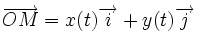
En un point où le vecteur dérivé

est non nul, il y a une tangente à la courbe, dirigée par ce vecteur.

L'interprétation cinématique classique est de considérer le paramètre t comme le temps, le vecteur dérivé est alors le vecteur vitesse.

Il convient alors de distinguer

• la courbe, qui est souvent appelée trajectoire, et qui est un sous-ensemble du plan ;
• l'arc paramétré proprement dit qui est la courbe munie de sa « loi de temps », c'est-à-dire le couple de fonctions x(t),y(t).

Remarque : La représentation graphique d'une fonction y=f(x) peut être vue comme un cas particulier de courbe paramétrée : en prenant comme paramètre l'abscisse elle-même (t=x), on a x(t)=t, y(t)=f(t).

Équation polaire

On utilise pour ce type de courbe les coordonnées polaires. La courbe est alors définie par une fonction et ses points ont pour coordonnées polaires .

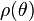
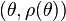
On peut facilement se ramener à une courbe paramétrée, d'équations . Mais les mathématiciens traitent ces courbes par des méthodes adaptées, en introduisant en premier lieu la notion de repère mobile.

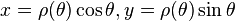
Équation cartésienne

Étant donnée une fonction f de x et de y, on appelle courbe d'équation cartésienne f(x,y)=C l'ensemble des points M(x,y) dont les coordonnées vérifient cette équation.

On parle aussi pour cet ensemble de la ligne de niveau C de la fonction f. Si la fonction f représente une altitude, on retrouve le concept familier de courbe de niveau d'une carte de géographie.

Par exemple la ligne de niveau R>0 pour la fonction est le cercle de centre O et de rayon R.

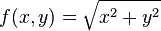
Le théorème des fonctions implicites permet de trouver l'équation de la tangente à cette courbe en un point donné. Précisément, un point M=(x,y) appartenant à la courbe est dit régulier quand le gradient de f est non nul en ce point. Et dans ce cas, la tangente est orthogonale au vecteur gradient.

Équation intrinsèque

Il s'agit de décrire une courbe par une équation reliant exclusivement les invariants euclidiens : abscisse curviligne, rayon de courbure (ou courbure), rayon de torsion (ou torsion). Pour les courbes planes, l'invariant de torsion n'intervient pas. À la différence des systèmes précédents, de telles équations déterminent par nature les courbes indépendamment de leur orientation dans l'espace : les courbes sont donc définies à un déplacement près. Les équations les plus simples déterminent en général des courbes de type spirale.

Exemples :

• s désignant l’abscisse curviligne et R le rayon de courbure,
  • R² + s² = 16a² (a donné) détermine une cycloïde,
  • (a donné) détermine une clothoïde,
  • (a donné) détermine une spirale logarithmique,