Courbe - Définition
La liste des auteurs de cet article est disponible ici.
Courbes algébriques
Liens externes
- Mathcurve.com (en français)
Considérations topologiques
Lorsqu'on relâche l'exigence de dérivabilité des fonctions définissant les courbes, la situation peut singulièrement se compliquer.
Un exemple surprenant : la courbe de Peano
![](https://static.techno-science.net/illustration/Definitions/1200px/p/peanocurve.svg_fde1f05703fea6b82d1c3cd8a5941163.png")
En 1890, Peano découvrit une « courbe » aux propriétés étranges :
- elle est définie par une application continue de [0,1] dans le plan ;
- sa trajectoire est l'ensemble des points du carré [0,1]x[0,1].
L'illustration représente les premières étapes de la construction de cette courbe, qu'on range aujourd'hui dans la catégorie des fractales.
Avec cet exemple, ou en considérant d'autres constructions de courbes fractales telles que le flocon de Koch ou la courbe du dragon, la notion de dimension semble perdre de sa pertinence. Il est possible en effet que l'image du segment [0,1] par une application continue ait une dimension de Hausdorff strictement supérieure à 1, ou même une mesure de Lebesgue différente de 0.
Théorème de Jordan
Même dans le cadre très général des courbes continues, un résultat de topologie à l'énoncé apparemment élémentaire reste vérifié : une boucle délimite un intérieur et un extérieur.
Dit en termes moins vagues, si une courbe continue ![f:[a,b]\to \R^2](https://static.techno-science.net/illustration/Definitions/autres/6/693e0884ce031d4c7db0f416a7f856e4_b6b227b26285bddd7690a3be3c354fea.png){kind=small}
est fermée (les deux extrémités coïncident) et simple (la fonction est injective sur [a,b[, c'est-à-dire la courbe ne se recoupe pas elle-même) alors elle sépare le plan en deux composantes connexes, l'une bornée (l'intérieur), l'autre non bornée (l'extérieur). De plus la courbe est la frontière (au sens topologique) de chacune de ces deux parties.
Ce théorème, ne connut une démonstration que tardivement (en 1905 par Oswald Veblen) après plusieurs tentatives incomplètes. Il convient de noter que la courbe de Peano n'est pas une courbe simple, même si les fonctions obtenues à chaque étape de sa construction le sont
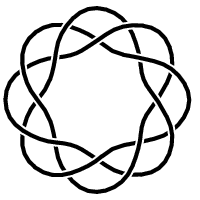
Plongement, nœud
Soit I un intervalle. L'application 
est appelée plongement lorsqu'elle réalise un homéomorphisme de I sur son image f(I). De même on parle de courbe fermée plongée pour une application 
définie sur le cercle unité et qui constitue un homéomorphisme sur son image.
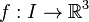
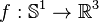
Il est possible de plonger le cercle de plusieurs façons, non équivalentes, dans l'espace de dimension trois. La classification des plongements possibles constitue la théorie des nœuds.