Mantisse - Définition

Le terme mantisse (du latin mantissa = addition) a plusieurs sens en mathématiques. On restera donc très vigilant quant à l'utilisation de ce terme.

Définition originelle

Originairement, le terme de mantisse concernait la différence entre un nombre et sa partie entière. Pour un décimal positif, la mantisse représentait alors sa partie fractionnaire

dans le nombre décimal 123,7585, la partie entière est 123 et la partie fractionnaire ou mantisse est 0,7585

dans le nombre décimal négatif - 17,228, la partie entière est -18 et la mantisse est 0,772

C'est avec ce sens que l'on parle de mantisse et caractéristique d'un logarithme décimal

dans log(123,7) = 2,09237, la caractéristique est 2 et la mantisse est 0,09237

dans log(0,001237) = - 2,90763, la caractéristique est -3 et la mantisse est 0,09237

La mantisse et la caractéristique d'un logarithme décimal est en rapport étroit avec l'écriture du nombre initial en notation scientifique : si x = a.10ⁿ avec a compris entre 1 et 10 (exclu) alors log(x) = n + log(a), n est alors la caractéristique et log(a) la mantisse de log(x)

C'est probablement l'écriture sous cette forme scientifique qui est à l'origine du glissement de sens du terme mantisse.

Sens actuel

En informatique, la nécessité de trouver une écriture des nombres compatible avec la taille mémoire qu'on lui attribue a privilégié la notation scientifique et l'écriture en virgule flottante.

Dans l'écriture en notation scientifique du nombre x, où a est un nombre compris entre 1 et 10 (exclu), le nombre a est communément appelé la mantisse de x (le terme correct est significande), n l'exposant de x et le signe de x.

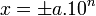
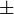
Un nombre décimal peut alors être connu avec une bonne précision par la donnée de ces trois valeurs : le signe, la mantisse et l'exposant.

Cependant, la base d'écriture des nombres en informatique est plus souvent la base binaire que la base décimale. On généralise alors la notion d'écriture scientifique à d'autres bases que la base 10: si et si a est compris entre 1 et b (exclu) alors est le signe de x, a est sa mantisse et n est son exposant dans la base b.

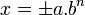
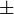
Exemples sur une calculatrice scientifique

Essayons d'obtenir une valeur approchée avec la calculatrice et regardons comment elle se comporte.

• Avec un nombre A supérieur à 10¹⁰:

1. Prenons A, le produit de deux entiers grands, 123456 et 654321 (écrire l'opération sur la machine).
2. Lorsqu'on appuye sur la touche Résultat de la calculatrice, celle-ci affiche X = 8,077...¹⁰ (ou 8,077...e+10 selon).
3. M et n sont parfaitement identifiables. Il faudrait donc écrire 8 x 10¹⁰

On peut aussi voir cela directement en tapant un nombre à plus de 10 chiffres.

• Avec un nombre B inférieur à 10^-3:

1. Prenons B, le quotient d'un entier petit par un grand, 2 et 3421 (écrire l'opération sur la machine).
2. Lorsqu'on appuye sur la touche Résultat de la calculatrice, celle-ci affiche X = 5,846...^-04 (ou 5,846...e-04 selon).
3. M et n sont aussi parfaitement identifiables. Il faudrait donc écrire 5 x 10^-4

On peut aussi voir cela directement en tapant un nombre inférieur à 0,001.