Élément entier - Définition
La liste des auteurs de cet article est disponible ici.
Propriétés
On dit qu'un morphisme de A dans B est un morphisme fini s'il fait de B un A-module de type fini, autrement dit, s'il existe
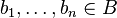
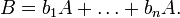
Théorème — Les conditions suivantes sont équivalentes :
- b est entier sur A,
- A[b] est fini sur A (en tant que A-module),
- il existe une sous-algèbre (unitaire) de B contenant b et finie sur A (en tant que A-module),
- il existe un A[b]-module fidèle et de type fini en tant que A-module.
-
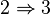
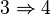
-
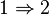
Soit
![P(X)=X^n+a_{n-1}X^{n-1}+\ldots+a_0\in A[X]](https://static.techno-science.net/illustration/Definitions/autres/3/3cc42664a9f4710e3204db468289d17e_474e35a29b11712952896376832ec0c7.png)
![F(X)\in A[X]](https://static.techno-science.net/illustration/Definitions/autres/9/9e3befefafa749d0424ee937b4322aa4_26b3b2d401edbc772ce3db1241b24aae.png)
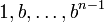
-
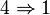
Soient D un tel module et
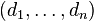
![\forall i \in [1, n],\quad b.d_i = \sum_{j=1}^n a_{ij}d_j](https://static.techno-science.net/illustration/Definitions/autres/a/acc352b9cdb9172dc1c97b840b9a130c_d13fe4dc3fc30c1097882a6dff152ac0.png)
ce qui s'écrit aussi
![\forall i \in [1, n],\quad \sum_{j=1}^n (\delta_{ij}b-a_{ij})d_j=0](https://static.techno-science.net/illustration/Definitions/autres/c/cc726dcd2fbfe38e7ebfd3093e9511a5_b9d93bcf98b12fe116af1978492e8bd8.png)
où δij désigne le symbole de Kronecker.
Si l'on note d le déterminant det(δijb − aij), la formule de Laplace montre que l'on a d.di = 0 pour tout i. Comme les di engendrent D, on en déduit d.D = 0 donc (puisque D est fidèle) d = 0. Si l'on développe ce déterminant d, on obtient bien une équation de la forme P(b) = 0, où P est un polynôme unitaire à coefficients dans A.
Corollaire 1 — L'ensemble des éléments de B entiers sur A est un sous-anneau de B contenant l'image de
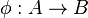
Si b et c sont entiers sur A alors la sous-algèbre A[b,c] est finie (en tant que module) sur A[b] qui lui-même est fini sur A, donc A[b,c] est fini sur A donc (d'après le théorème) tous ses éléments sont entiers sur A, en particulier les éléments b-c et bc.
Corollaire 2 — Si B est entier sur A (c'est-à-dire si tous ses éléments sont entiers sur A), et si c est un élément entier sur B d'une B-algèbre, alors c est entier sur A. Ainsi un anneau entier sur un anneau entier sur A est entier sur A.
Soit
![X^n+b_{n-1}X^{n-1}+\ldots+b_0\in B[X]](https://static.techno-science.net/illustration/Definitions/autres/3/367f7ba9c60d5390b0e57a2e44fde452_608927fb159da365d75e99c9df37ccf2.png)
![C=A[b_0,\ldots,b_{n-1}]](https://static.techno-science.net/illustration/Definitions/autres/b/b63bbbe237d155926ea2627a2bf76639_cc0a0f78d3b93ab11b80c5823491dc5e.png)
- Si B est entier sur A, alors pour toute A-algèbre C, le produit tensoriel
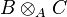
- Si de plus C est entier sur A, alors
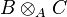
Applications à la géométrie algébrique
Soit
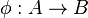
- Les dimensions de Krull vérifient l'inégalité
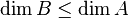
- Le morphisme de schémas
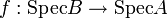
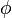
- Si de plus
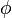
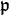
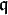
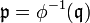
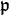
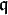
Lien avec les extensions algébriques
- Soient A un anneau factoriel, K son corps des fractions, et L une extension de K. Un élément de L est entier sur A si et seulement s'il est algébrique sur K et si son polynôme minimal est à coefficients dans A.
- Soient A un anneau intègre, K son corps des fractions, L une extension finie de K, et B la fermeture intégrale de A dans L. L'une des deux conditions suivantes suffit pour que B soit fini sur A :
- - l'extension est séparable, ou
- - A est une algèbre intègre de type fini sur un corps ou un anneau de Dedekind de caractéristique nulle.

















































