Élément entier - Définition

Introduction

En mathématiques, et plus particulièrement en algèbre commutative, les éléments entiers sur un anneau commutatif sont à la fois une généralisation des entiers algébriques (les éléments entiers sur l'anneau des entiers relatifs), et des éléments algébriques dans une extension de corps. C'est une notion très utile en théorie algébrique des nombres et en géométrie algébrique. Son émergence a commencé par l'étude des entiers quadratiques, en particulier les entiers de Gauss, ceux d'Eisenstein et ceux de Dirichlet.

Définition

On fixe un anneau commutatif unitaire A. Soit B une A-algèbre commutative (c'est-à-dire un anneau commutatif unitaire muni d'un morphisme d'anneaux ). Un élément b de B est un élément entier sur A s'il existe un polynôme unitaire à coefficients dans A s'annulant sur b.

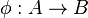
Exemples

• Lorsque A,B sont des corps (commutatifs), les éléments entiers sont exactement les éléments algébriques.
• Dans le cas du corps vu une algèbre sur l'anneau des entiers relatifs, les éléments entiers sont les entiers algébriques. Par exemple tout entier de Gauss avec et i une racine carré de − 1, est entier sur . Concrètement, α est annulé par le polynôme unitaire à coefficients entiers

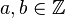
• La variable T de l'anneau des polynômes n'est pas un élément entier sur .
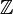
• Une fraction rationnelle est entière sur si et seulement si c'est un entier rationnel.
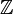
• Soit A = k[T] l'anneau des polynômes à coefficients dans un corps k, soit B = A[S] / (S² − T³ − 1)A[S]. Alors la classe s de S dans B est entière sur A, c'est un zéro du polynôme .

On dit que B est entier sur A, ou que c'est une A-algèbre entière si tout élément de B est entier sur A. On dira aussi que est un morphisme entier ou que est une extension entière.

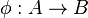
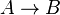
Contrairement au cas des extensions de corps, un morphisme d'anneaux n'est pas nécessairement injectif. Mais dire que b est entier sur A revient à dire que b est entier sur le sous-anneau de B. On peut donc toujours se restreindre aux morphismes injectifs. Mais il est plus commode de garder la définition du cas général (on peut ainsi dire qu'un morphisme surjectif est entier).

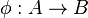
Fermeture et clôture intégrales

D'après le corollaire 1 ci-dessus, l'ensemble des éléments de B entiers sur A est une sous-A-algèbre de B (c'est-à-dire un sous-anneau de B stable par la multiplication par A). Cet ensemble est appelé la fermeture intégrale de A dans B.

Si A est intègre, sa fermeture intégrale dans son corps des fractions est appelée la clôture intégrale de A. En géométrie algébrique, cela correspond à la normalisation du schéma défini par A. Si A est égal à sa clôture intégrale, on dit que A est intégralement clos ou normal.

Exemples

• L'anneau Z des entiers est intégralement clos, l'anneau Z[i] des entiers de Gauss aussi. En fait tout anneau principal est intégralement clos.

• Plus généralement un anneau factoriel est intégralement clos (par exemple un anneau régulier, comme l'anneau de polynômes à coefficients dans un corps ou anneau principal R).

• La clôture intégrale de est .

• Un anneau de valuation est intégralement clos, une intersection d'anneaux de valuation aussi.

En fait, un anneau intègre est intégralement clos si et seulement si c'est une intersection d'anneaux de valuation pour son corps des fractions.

• Un anneau de Dedekind est intégralement clos (par définition ! ).
• Soit A un anneau intègre. La fermeture intégrale de A dans une extension de son corps des fractions est toujours intégralement close. Cela résulte du corollaire 2 ci-dessus. En particulier, la clôture intégrale de A est intégralement close.

• « Le passage aux anneaux de fractions commute à la fermeture intégrale : soit A un sous-anneau d'un corps K, et soit S une partie multiplicative de A ne contenant pas 0. Pour qu'un élément de K soit entier sur S^-1A, il faut et il suffit qu'il soit de la forme a' / s où a' est entier sur A, et où s appartient à S ». En particulier :
  • si A est intégralement clos alors S^-1A aussi ;
  • dans K, la fermeture algébrique du corps des fractions de A est égale au corps des fractions de la fermeture intégrale de A.

Si x est entier sur S^-1A alors il vérifie une équation de la forme

.

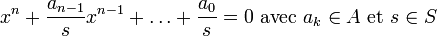
En multipliant par sⁿ, on en déduit que sx est entier sur A. La réciproque se prouve de même en reprenant ce calcul en sens inverse. Le premier cas particulier s'obtient en prenant K égal au corps des fractions de A, et le second en prenant S égal à l'ensemble des éléments non nuls de A.