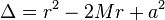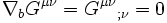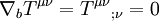Équation d'Einstein - Définition

Propriétés de l'équation d'Einstein

Conservation de l'énergie et du moment

Une importante conséquence de l'équation d'Einstein est la conservation locale de l'énergie et du moment. Ce résultat apparaît en utilisant l'identité différentielle de Bianchi pour obtenir :

ce qui, en utilisant l'équation d'Einstein, donne :

qui exprime la conservation locale du tenseur énergie-impulsion.

Non-linéarité des équations de champ

L'équation d'Einstein donne lieu à 10 équations aux dérivées partielles non-linéaires pour les composants métriques. Cette caractéristique de non-linéarité distingue la relativité générale de l'ensemble des autres théories physiques. Par exemple, les équations de Maxwell de l'électromagnétisme sont linéaires par rapport aux champs électriques et magnétiques (c'est-à-dire que la somme de deux solutions est aussi une solution). Un autre exemple est celui de l'équation de Schrödinger en mécanique quantique où l'équation est linéaire par rapport à la fonction d'onde.

Le principe de correspondance

L'équation d'Einstein se réduit aux lois de la gravité de Newton en utilisant l'approximation des champs faibles et des mouvements lents.

Solutions de l'équation

Les solutions de l'équation d'Einstein sont les tenseurs métriques de l'espace-temps. Elles sont souvent appelées "métriques". Elles décrivent la structure de l'espace-temps en incluant le mouvement inertien des objets. Du fait que les équations de champs ne sont pas linéaires, elles sont très souvent difficiles à résoudre (c'est-à-dire sans faire des approximations). Par exemple, il n'existe pas de solution complète connue pour un espace-temps constitué de deux corps massifs (correspondant au modèle théorique d'un système binaire de deux étoiles par exemple). Cependant, des approximations sont généralement faites dans ces cas.

L'étude des solutions exactes des équations de champs d'Einstein est l'une des activités de la cosmologie. Elle a mené à la prédiction de l'existence de trous noirs et aux divers modèles de l'évolution de l'univers.

Espace vide

Dans le cas où une région de l'espace est vide (c'est-à-dire que le tenseur énergie-impulsion T_ab est nul) et loin de toute source gravitationnelle, la métrique de Minkowski s'applique. Cette dernière est la forme classique qu'on trouve dans le cadre de la relativité restreinte et les distances se mesurent à l'aide de la métrique:

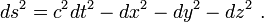
On voit alors qu'on a

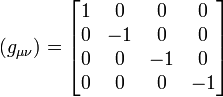
Espace autour d'une masse sphérique

La métrique de Schwarzschild permet de décrire la déformation de l'espace-temps dans le vide autour d'une masse sphérique unique (par exemple une étoile). On a alors, pour (x⁰,x¹,x²,x³) = (ct,r,θ,φ) :

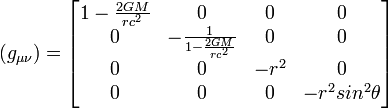
Espace autour d'un corps en rotation

La métrique de Kerr, pour sa part, décrit la déformation de l'espace-temps dans le vide autour d'un trou noir en rotation (en l'absence de champs électromagnétiques). Elle est l'œuvre en 1963 de Roy Kerr, mathématicien néo-zélandais. Contrairement à la métrique de Schwarzschild qui peut s'appliquer autour de tout corps sphérique et statique, la métrique de Kerr est spécifique aux trous noirs seulement et ne peut s'appliquer à d'autres corps en rotation. En prenant à nouveau un référentiel sphérique de l'espace-temps (x⁰,x¹,x²,x³) = (t,r,θ,φ) (en prenant c=1) on a :

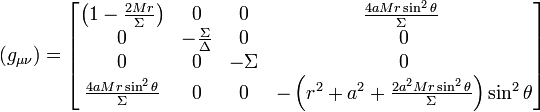
avec

,

,
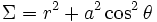