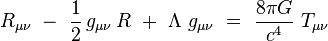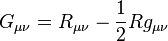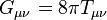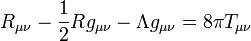Équation d'Einstein - Définition

Introduction

L'équation d'Einstein ou équation de champ d'Einstein est l'équation aux dérivées partielles principale de la relativité générale. C'est une équation dynamique qui décrit comment la matière et l'énergie modifient la géométrie de l'espace-temps. Cette courbure de la géométrie autour d'une source de matière est alors interprétée comme le champ gravitationnel de cette source. Le mouvement des objets dans ce champ est décrit très précisément par l'équation de sa géodésique.

Forme mathématique de l'équation de champ d'Einstein

L'équation de champ d'Einstein est généralement écrite de la manière suivante :

.

où R_μν est le tenseur de Ricci, R la courbure scalaire, g_μν le tenseur métrique de signature (+,-,-,-), Λ la constante cosmologique, G la constante gravitationnelle (environ 6,6742.10^-11 m³kg^-1s^-2), c la vitesse de la lumière (exactement 299 792 458 m.s^-1), π le nombre pi et T_μν le tenseur énergie-impulsion.

L'équation de champ d'Einstein est une équation de tenseur reliant un ensemble de tenseurs symétrique 4 x 4. Elle est écrite en termes de composants. Chaque tenseur a 10 composants indépendants. Vue la liberté de choix relative aux coordonnées d'un espace-temps à 4 dimensions, on n'aboutit qu'à 6 équations indépendantes.

L'équation de champ d'Einstein est comprise comme une équation permettant de connaître le tenseur métrique g_ab, étant donnée une distribution de matière et d'énergie exprimée sous la forme d'un tenseur énergie-impulsion. Malgré son aspect simple, elle est en réalité relativement complexe, notamment du fait que le tenseur de Ricci et la coubure scalaire dépendent de la métrique.

Λ, la constante cosmologique, a été introduite par Einstein pour permettre des solutions statiques au modèle cosmologique issu de l'équation d'Einstein. Par la suite, il a qualifié cette introduction de «plus grande erreur de sa vie».

Si on considère que Λ = 0 (ce qu'Einstein a fini par admettre, mais qui est controversé aujourd'hui), il est possible d'écrire cette relation de manière plus compacte en définissant le tenseur d'Einstein

qui est un tenseur symétrique de rang 2 dépendant de la métrique. En travaillant en unité géométrique où G = c = 1, on a alors :

La partie de gauche représente la courbure de l'espace-temps telle qu'elle est déterminée par la métrique et l'expression de droite représente le contenu masse/énergie de l'espace temps. Cette équation peut alors être interprétée comme un ensemble d'équations décrivant comment la courbure de l'espace-temps est reliée au contenu masse/énergie de l'univers.

Ces équations, ainsi que l'équation de la géodésique, forment le cœur de la formulation mathématique de la relativité générale.

Il faut y ajouter une loi dynamique pour avoir une théorie complète.

La constante cosmologique

Il est possible de modifier l'équation des champs d'Einstein en introduisant un terme proportionnel à la métrique :

(on précisera que cette équation est vraie dans un système d'unité tel que c=1) La constante Λ est appelée la constante cosmologique.

Cette constante cosmologique était à l'origine introduite par Einstein pour obtenir de son équation un univers statique (c'est-à-dire un univers qui ne soit pas en expansion ou en contraction). Cet effort fut un échec pour deux raisons : l'univers statique décrit par cette théorie était instable, et les observations des galaxies distantes par Hubble une décennie plus tard confirmèrent que notre univers n'est en fait pas statique mais en expansion. Λ fut donc par la suite abandonné, et Einstein la qualifia de "la plus grande erreur de sa vie".

Bien que la motivation d'Einstein pour l'introduction de cette constante ait été erronée, sa présence dans l'equation n'est pas inconsistante. En effet, récemment les techniques astronomiques améliorées ont permis d'affirmer qu'une valeur non nulle de Λ est nécessaire pour expliquer certaines observations. L'existence d'une constante cosmologique est alors équivalente à l'existence d'une énergie du vide non nulle.