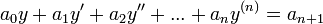Équation linéaire - Définition

Dans les équations différentielles

On parlera ici de fonctions définies sur ou sur à valeurs dans ou dans .

Une équation différentielle linéaire du premier ordre d'inconnue y est une équation de la forme ay + by' = c où a, b et c sont des fonctions numériques.

Une équation différentielle linéaire d'ordre n et d'inconnue y est une équation de la forme

où , , ... , sont des fonctions numériques et y^(k) la dérivée d'ordre k de y.

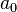
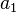
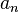
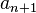
Si , , ... , sont des constantes, on parle d'équation linéaire à coefficients constants.

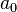
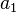
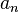
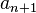
Cas des équations homogènes

Si a_{n + 1} = 0 on parle d'équation linéaire homogène.

Par exemple l'équation différentielle y" + y= 0 est une équation différentielle linéaire homogène à coefficients constants.

Si y₁ et y₂ sont solutions d'une équation différentielle linéaire homogène alors il en est de même de ky₁ et de y₁ + y₂;

Si on connaît une solution particulière d'une équation différentielle linéaire, la solution générale est formée de la somme de cette solution particulière avec la solution générale de l'équation linéaire homogène associée.

Dans les équations algébriques

Une équation linéaire à une inconnue x est une équation de la forme où a et b sont des réels (ou des complexes). Les réels a et b sont appelés des coefficients, a est le coefficient devant x et b le coefficient constant. On appelle aussi cette équation, une équation du premier degré à une inconnue.

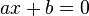
Une équation linéaire à plusieurs inconnues x, y, z ...est une équation de la forme où a, b, c, ... k sont des réels (ou des complexes). De même ici, a est le coefficient devant x, b le coefficient devant y, ..., k le coefficient constant.

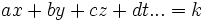
L'ensemble des solutions d'une équation linéaire à n inconnues dont au moins un coefficient autre que le coefficient constant est non nul, est un sous-espace affine de dimension n - 1.

Cas des équations linéaires homogène

Les équations linéaires homogènes sont celles dont le coefficient constant est nul.

Propriété: si (x, y, z, ....) et (x', y', z', ...) sont deux solutions d'une équation linéaire homogène alors il en est de même de (kx, ky, kz, ...) et (x + x', y + y', z + z', ...).

L'ensemble des solutions d'une équation linéaire homogène à n inconnues dont un coefficient au moins est non nul est un sous-espace vectoriel de dimension n - 1.

Voir aussi : Système d'équations linéaires