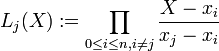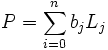Équation linéaire - Définition
La liste des auteurs de cet article est disponible ici.
Introduction
Une équation à coefficients réels ou complexes est dite linéaire quand elle peut être présentée sous la forme a.x=b, où x est l'inconnue, a et b sont deux nombres donnés. Si a est différent de zéro, la seule solution est le nombre b/a.
Plus généralement, une équation est dite linéaire lorsqu'elle se présente sous la forme u(x)=b, où u est une application linéaire entre deux espaces vectoriels E et F, b est un élément donné de F. On recherche l'inconnue x dans E.
La linéarité permet d'effectuer des sommes et des combinaisons linéaires de solutions, ce qui est connu en physique sous le nom de principe de superposition. Les espaces de solutions ont des structures d'espaces vectoriels ou affines. Les méthodes de l'algèbre linéaire s'appliquent et peuvent considérablement aider à la résolution.
Résolution générale
Soient u application linéaire de E dans F, et b appartenant à F. On considère l'équation linéaire u(x)=b.
L'équation u(x)=0, dite équation homogène associée a pour solution le noyau de u, qui est un sous-espace vectoriel de E.
L'équation complète u(x)=b
- a des solutions si et seulement si

- dans ce cas l'espace des solutions est un espace affine, dirigé par le noyau. En notant x0 une solution particulière de l'équation complète, l'espace solution est de la forme
Ce qu'on retient souvent sous la forme « la solution de l'équation complète est la somme d'une solution particulière et de la solution générale de l'équation homogène associée ».
Relations image-noyau
La résolution de l'équation revient donc à la détermination des espaces image et noyau de u. Le noyau est souvent plus facile à calculer que l'image, mais celle-ci peut être connue dans de nombreux cas grâce au théorème suivant.
Théorème d'isomorphisme des supplémentaires du noyau
Soit u application linéaire de E dans F. Soit H un supplémentaire du noyau de u. Alors H est isomorphe à l'image de u. Plus précisément, la restriction de u à H induit un isomorphisme de H sur Im u.
Corollaire : relation rang-noyau
Avec les mêmes notations si en outre l'espace de départ E est de dimension finie
Cette formule est parfois appelée formule du rang. Ou même, plus généralement, si le noyau est de codimension finie, cette codimension est égale à la dimension de l'image.
Superposition de solutions
Si on additionne une solution de u(x)=b et une solution de u(x)=c, on obtient une solution de l'équation u(x)=b+c. On peut plus généralement effectuer des combinaisons linéaires de solutions, ce qui porte souvent le nom de superposition en physiques.
Ainsi si on doit résoudre u(x)=b pour un vecteur b général, on constate qu'il suffit d'effectuer la résolution pour les vecteurs b d'une base de F.
On peut essayer d'étendre la méthode de superposition à des « sommes infinies », c'est-à-dire des séries. Mais il faut alors justifier qu'on peut effectuer un passage à la limite.
Exemple d'application : interpolation de Lagrange
Soient n+1 scalaires distincts x0, ..., xn et n+1 scalaires y0, ..., yn. La recherche des polynômes P tels que pour tout i, P(xi)=yi est appelée problème d'interpolation de Lagrange.
Il s'agit d'un problème linéaire avec
Le noyau de u est l'ensemble des polynômes nuls en x0, ..., xn
Il admet pour supplémentaire l'espace
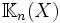
En conséquence l'image de u est de dimension n+1, ce qui prouve que u est surjective et que le problème a toujours une solution. En outre
est un isomorphisme d'espaces vectoriels.
On en déduit les résultats d'existence et d'unicité suivants
- le problème d'interpolation de Lagrange admet toujours des polynômes solutions
- un seul des polynômes solutions est de degré inférieur ou égal à n
- les autres s'en déduisent par ajout d'un multiple du polynôme (X-x0). ... . (X-xn)
Enfin l'isomorphisme u1 peut être utilisé pour obtenir explicitement le polynôme d'interpolation de plus bas degré. Cela revient à déterminer l'antécédent de b par u1. Par linéarité, il suffit de déterminer les antécédents des vecteurs de la base canonique de
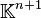
Il est donc naturel de faire intervenir le problème d'interpolation élémentaire : trouver
On aboutit alors naturellement à l'expression suivante
Et enfin pour le problème d'interpolation complet
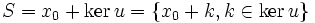
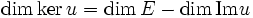
![u:\begin{matrix}\mathbb{K}[X]& \longrightarrow & \mathbb{K}^{n+1}\\ P&\longmapsto & (P(x_0), \dots, P(x_n))\end{matrix}\qquad b=(y_0, \dots, y_n)](https://static.techno-science.net/illustration/Definitions/autres/4/444beef80ba85d752ce8afcad4b03702_b9479f110d1b53798ae9f9d46bfd1238.png)
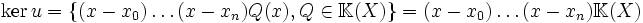
![u_1:\begin{matrix}\mathbb{K}_n[X]& \longrightarrow & \mathbb{K}^{n+1}\\ P&\longmapsto & (P(x_0), \dots, P(x_n))\end{matrix}](https://static.techno-science.net/illustration/Definitions/autres/7/76ab9d89c46b34dee4203b2958dc2d3c_e569f3a2477e10b4f2d0112c81853551.png)
![L_j \in \mathbb{K}_n[X]\hbox{ tel que } \forall i,\, 0\leq i \leq n , \, L_j(i)=\delta_{i,j}](https://static.techno-science.net/illustration/Definitions/autres/0/0b97a6f69008b7c417bb1bfdbf801872_8a8c3b4ce7650d0ec5de38bbb2a36ae0.png)