Équilibre chimique - Définition

Introduction

Un système chimique est à l'équilibre lorsque les variables intensives qui le décrivent (température, pression et activités chimiques des réactifs et des produits) sont homogènes dans tout le système et restent constantes au cours du temps.

Une réaction chimique ne se traduit pas toujours par la disparition complète des réactifs en étant qualifiée alors de réaction totale. De nombreuses réactions sont partielles et aboutissent à un équilibre entre les réactifs de départ et les produits de la réaction. L'ampleur de la réaction est caractérisé par l'état d'avancement : . Lorsqu'une réaction est équilibrée, cela signifie que la vitesse de la réaction dans le sens réactifs-produits est égale à la vitesse de la réaction dans le sens produits-réactifs. 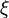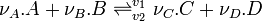L'état d'équilibre obtenu dans ce cas peut être qualifié de dynamique ou stationnaire.

où sont des espèces chimiques, les coefficients stœchiométriques et les vitesses de réaction.

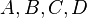
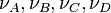
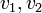
Dans le cas de réactions élémentaires, c'est-à-dire s'effectuant en une seule étape, les vitesses dépendent des concentrations , des espèces en présence, selon les expressions:

L'égalité des vitesses des réactions opposées entraîne la relation suivante:

Guldberg et Waage (1865), en s'inspirant de propositions de Berthollet, ont ainsi montré empiriquement qu'il existait une relation entre les concentrations des espèces présentes à l'équilibre en solution.

La constante d'équilibre , relative aux concentrations, a été appelée constante de Guldberg et Waage ou constante de la loi d'action des masses.

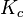
Le développement ultérieur de la thermodynamique et l'application de la fonction enthalpie libre : G aux réactions chimiques effectuées à température et pression constante, a permis de démontrer cette loi d'action des masses et d'établir la relation formulée empiriquement par Guldberg et Waage. Pour cela, il est nécessaire de définir précisément des grandeurs de réaction indispensables à la compréhension des phénomènes : enthalpie libre de réaction, , enthalpie libre standard de réaction, , quotient de réaction, et constante d'équilibre, . Ces outils permettent alors de prévoir le sens d'une réaction, le positionnement de l'équilibre et la composition du système.

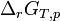
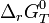
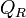
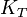
Le développement mathématique qui suit est plutôt difficile, mais il est essentiel pour comprendre les relations, leurs conditions d'application et leurs limites.

Réaction chimique et avancement de réaction

Considérons une réaction chimique effectuée à température et pression constantes dont l'équation bilan est la suivante:

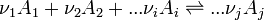
Les constituants du premier membre (réactifs) sont indicés ; ceux du second membre (produits) étant indicés .

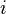
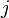
Lorsque la réaction progresse les constituants disparaissent alors que se forment les constituants . Considérons une petite progression caractérisée par une variation élémentaire de l'état d'avancement, de la réaction, et appelons , les variations élémentaires du nombre de moles de chaque constituant, à ce stade de la réaction.

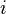
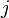
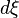
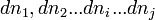
La réaction progresse en respectant la stœchiométrie de l'équation bilan ce qui implique que tous les rapports sont égaux au signe près.

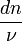
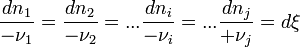
La variable peut donc être définie sur l'un quelconque des constituants et il existe une relation entre et chaque constituant. La connaissance de permet donc de connaître la composition du système. C'est donc une variable de composition.