Espace réciproque - Définition

Utilisation en cristallographie

Un cristal est un réseau tridimensionnel d'atomes, d'ions ou de molécules. Chaque nuage électronique va provoquer de la diffusion Rayleigh, qui va être équivalent à la réflexion et à la transmisison des réseaux de trait. Le cristal est donc en quelques sortes un réseau qui fonctionne en réflexion et en transmission.

Le lieu des extrémités des vecteurs de diffraction est donc une sphère complète, et non une demie sphère.

Indexation du réseau réciproque et plans de l'espace réel

Dans le cas d'un réseau de diffraction 3d (réseau de points dans l'espace), le réseau réciproque est également un réseau 3d. Chaque point du réseau réciproque ayant des coordonnées entières dans la base , on peut indexer chaque point par ses coordonnées.

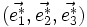
À chaque point du réseau réciproque est donc associé trois indices, notés habituellement (h, k, l), qui sont ses coordonnées.

Note

Jusqu'ici, les coordonnées entières étaient notées (a, b, c) afin d'éviter la confusion entre le vecteur d'onde et l'indice réel k.

Nous avons vu que dans l'espace réel, ce qui importait, c'était le réseau de points, et que ces points pouvaient être les nœuds de quadrillages parallèles entre eux.

Prenons un point A(h, k, l) de l'espace des phases. La droite (O,A), passant par l'origine et par A, peut être vue comme l'image d'un réseau plan (cf. section ) ; ce réseau plan est porté par une famille P de plans parallèles.

Cette famille de plans de l'espace réel a pour image une famillede plans de l'espace réciproque (cf. section ). On peut donc dire que A représente une famille de plans parallèles équidistants ; plus A est éloigné de l'origine, plus les plans sont rapprochés.

Il est ainsi possible d'indexer les plan imaginaires contenant des nœuds du réseau réel : les plans associés à A portent les indices (h, k, l).

On peut montrer que ces indices sont les Indices de Miller (voir cet article pour la démonstration).