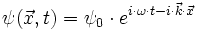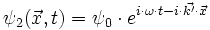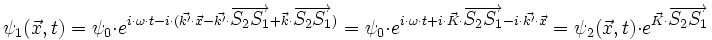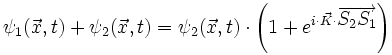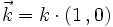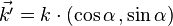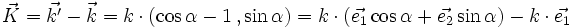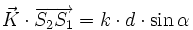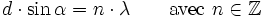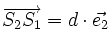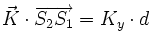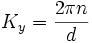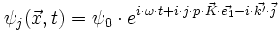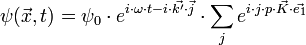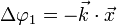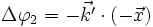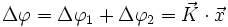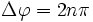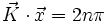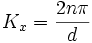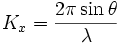Espace réciproque - Définition
La liste des auteurs de cet article est disponible ici.
Exemples
Exemple des fentes de Young
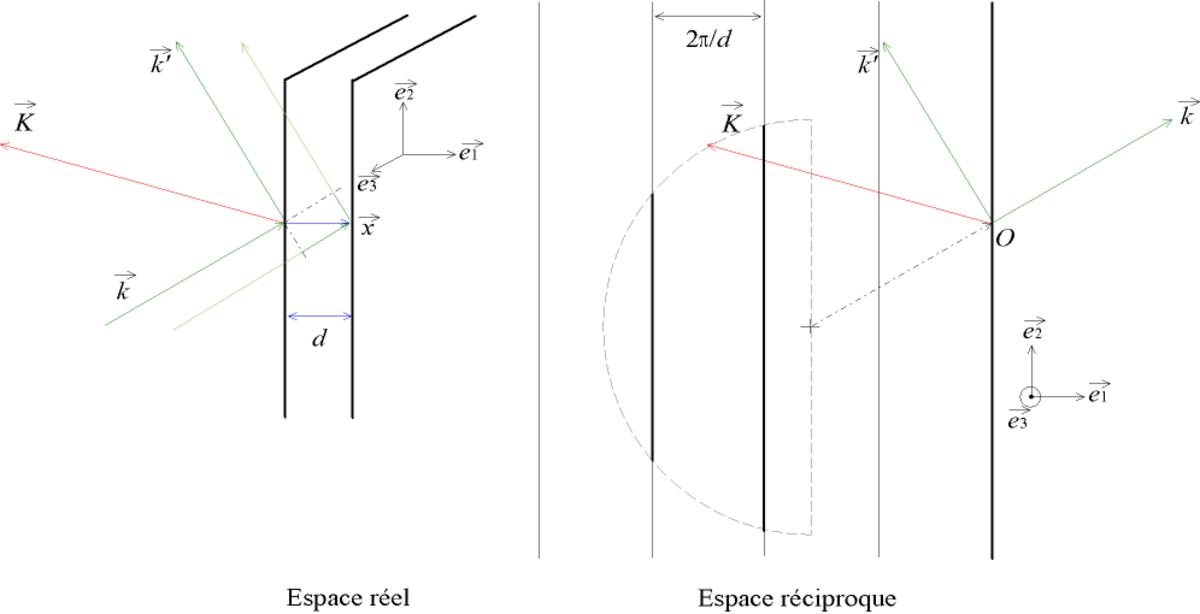
Le problème des fentes de Young peut se traiter avec ce formalisme si l'on considère que l'onde incidente est plane et que l'écran est à l'infini.
L'onde incidente a pour équation :
Si
- les fentes ont pour coordonnées S1(0,d) et S2(0,0) (on place l'origine à la fente du bas),
- le vecteur d'onde incident a pour composantes
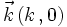
alors en
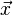
et celle diffusée par S1 vaut
où
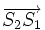
L'amplitude de l'onde dépend du facteur de droite, donc du produit scalaire
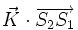
![\alpha \in\,]-\,\pi/2\,, \pi/2[](https://static.techno-science.net/illustration/Definitions/autres/a/a868f2953f4f9c76294c8af926f13cfa_2d7f35700793a94f8ef7847e745cff81.png)
donc
on remarque ici que la pointe du vecteur

![\alpha \in\,]\,\pi/2\,, \pi/2[](https://static.techno-science.net/illustration/Definitions/autres/d/dc6a05526b78a4efeb8b0ddb1291b006_e2abd439b0574e3c3a23a89e5ad9ff6c.png)

D'après l'équation qui précède, on a :
L'amplitude de l'onde est maximale lorsque le produit scalaire est un multiple de 2π. Comme k = 2π/λ, on retrouve bien que
Par ailleurs, on a :
et donc
La condition de diffraction devient alors
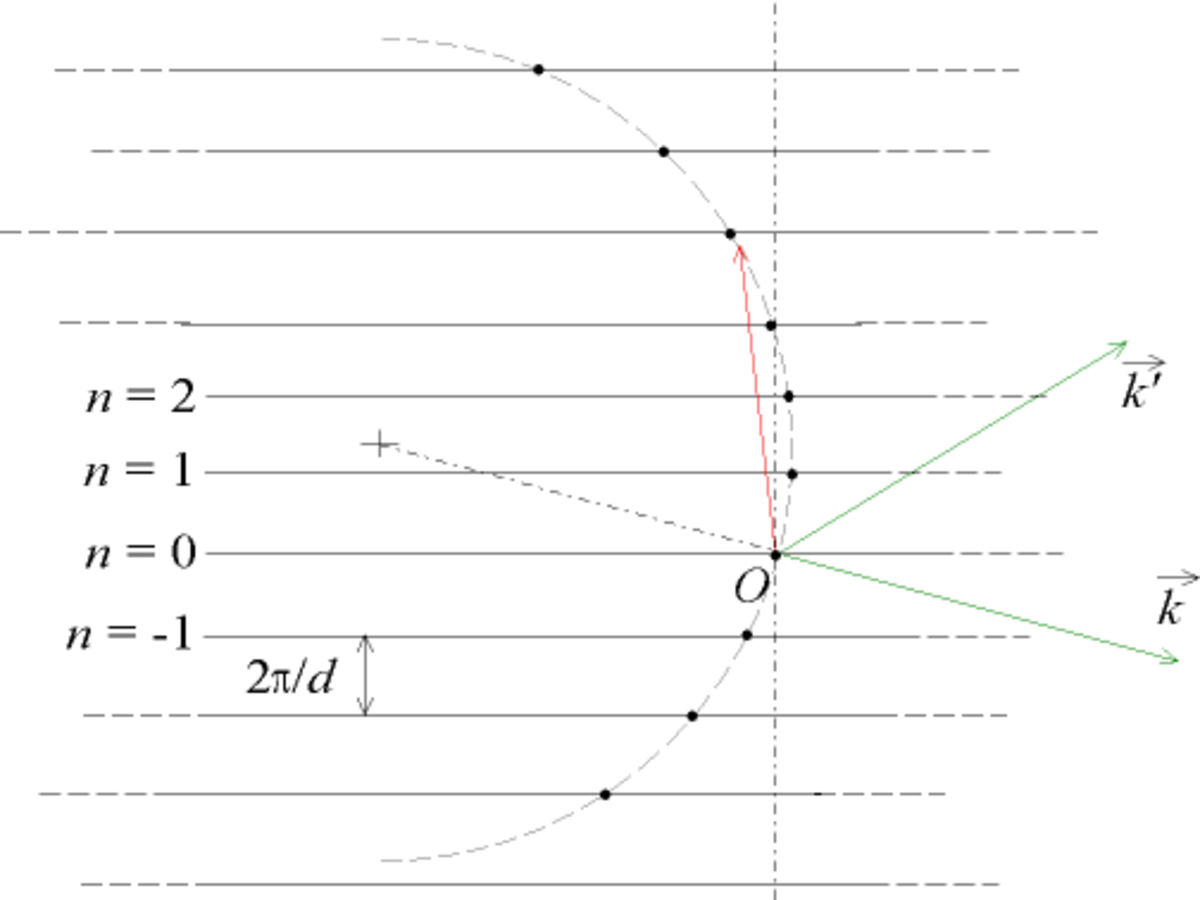
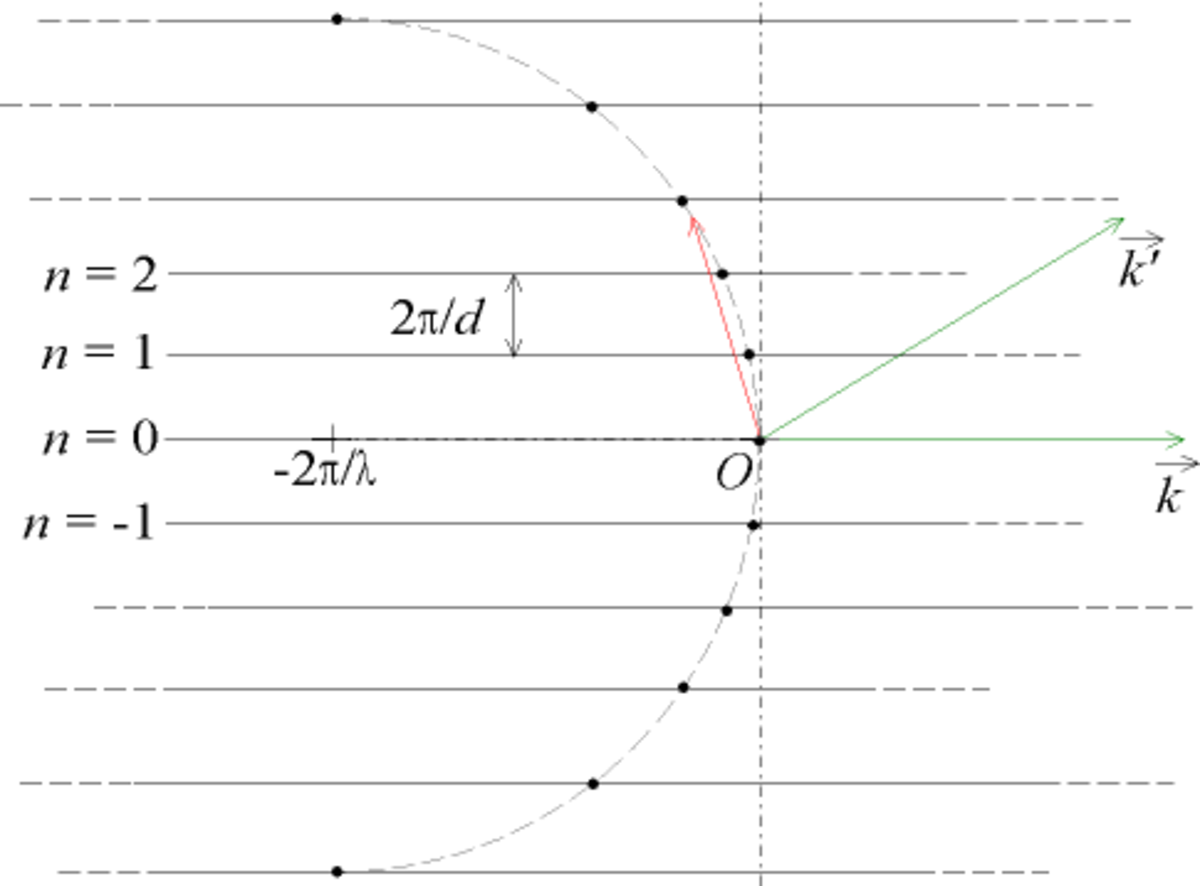
donc pour les conditions d'intensité maximale, Ky ne dépend que de n et pas de λ.
Les conditions sur

(-k = -2π/λ , 0) et de rayon k = 2π/λ avec les droites horizontales d'équation Ky = 2πn/d.
On voit donc que le système des fentes de Young d'écartement d, éclairées par onde incidente de longueur d'onde λ, peut se représenter par un ensemble de points (K1, K2..., Kn), définissant l'extrémité des vecteurs

La construction du réseau réciproque prend en compte uniquement le vecteur de diffraction


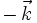
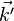
On peut même s'afranchir de l'invariance par translation et travailler en trois dimensions, en considérant des rayons (incidents ou diffractés) hors du plan
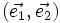
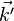

Ce réseau de plans horizontaux est le réseau réciproque des fentes de Young. On remarque que :
- les plans du réseau réciproque sont perpendiculaires au vecteur de translation
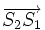
- l'espacement des droites est inversement proportionnel à l'espacement des fentes.
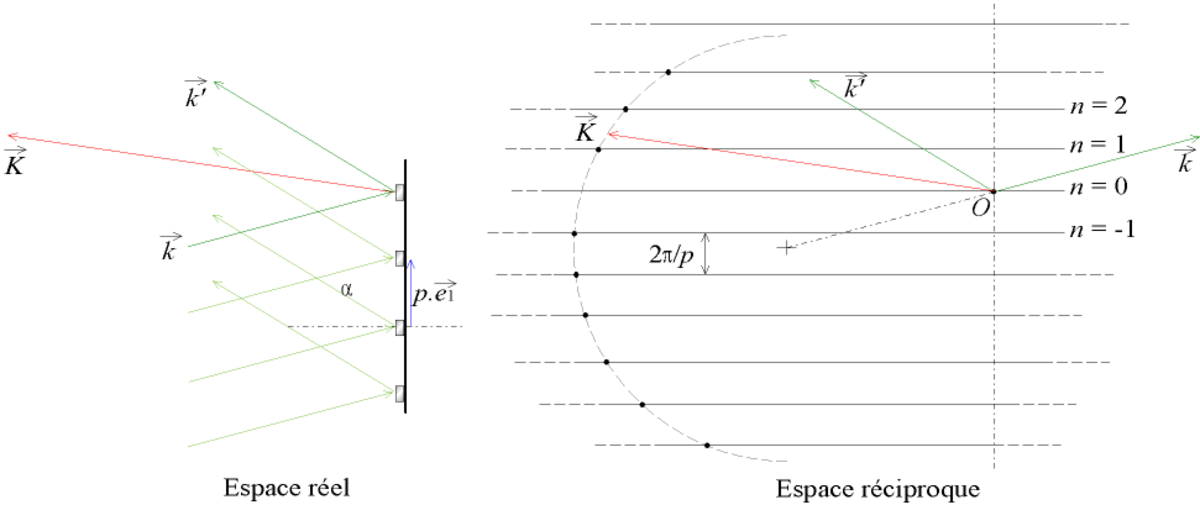
Exemple du réseau de diffraction
Considérons un réseau de diffraction optique de pas p.
Pour le calcul, on définit la fonction de l'onde diffractée par le j e trait par
si p est le pas du réseau et
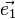
soit
Les conditions de diffraction sont similaires à celles des fentes de Young, seule change la largeur des raies. Le réseau réciproque est donc le même. Toutefois, on travaille fréquemment en réflexion. Dans ce cas-là, c'est le demi-cercle complémentaire qu'il faut envisager.
Exemple des interférences par une lame d'air
Les interférences par une lame d'air sont créées par la réflexion selon deux plans parallèles séparées d'une distance d. On regarde les interférences « à l'infini ».
Soit

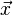
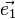
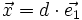
Le rayon frappant le plan superficiel est directement diffusé. Le rayon frappant le plan profond est diffusé après avoir subi un déphasage Δφ1
Considérons un vecteur d'onde diffusé
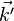
Le déphasage total est donc
L'interférence est constructrice si
c'est-à-dire si
donc
si Kx est la composante de

Comme précédemment, pour un vecteur incident



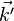
- Note
- Contrairement aux cas précédents, il n'y a plus ici d'invariance par translation selon l'axe des z, il faut donc se placer en trois dimensions.
On peut considérer un nombre « infini » de plan parallèles, et donc une sorte de réseau de plans. La différence serait alors la même qu'entre les fentes de Young et le réseau plan : les positions de diffraction sont les mêmes, seule change la largeur des raies.
Dans le cas où l'on considère une direction de diffusion symétrique à la direction d'incidence, et si l'on note θ l'angle entre le rayon incident et le plan, on a
(