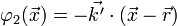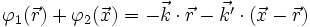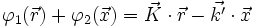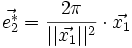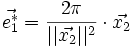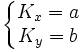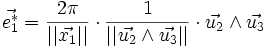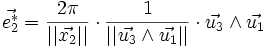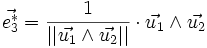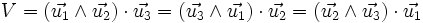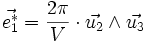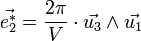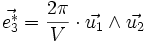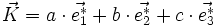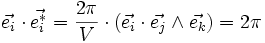Espace réciproque - Définition

Diffusion Rayleigh et principe de Huygens d'une onde

L'espace réciproque n'est utile que lorsque l'on considère une onde monochromatique. Cette onde est représentée par un vecteur unique.

Lorsque cette onde interagit avec une particule, elle peut être diffusée de manière élastique, par diffusion Rayleigh. De manière générale, pour une onde plane, on peut considérer en tout point une diffusion isotrope selon le principe de Huygens.

Les vecteurs diffusés ont la même norme que mais une direction différente ; dans l'espace réciproque, leur extrémité forme une sphère de rayon . On ne s'intéresse qu'à une direction de diffusion à la fois, donc à un seul vecteur .

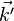
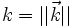
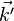
Considérons un centre de diffusion situé en . Le déphasage spatial par rapport à l'origine est

.

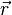
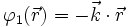
Si l'on s'intéresse au déphasage de l'onde diffusée en un point , le déphasage spatial entre la source et le point vaut

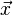
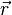
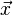
puisque l'onde a parcouru un chemin . Le déphasage total en vaut donc

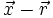
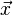
si l'on pose

on obtient

on a donc un terme qui ne dépend que de la position du centre de diffusion, et un autre terme qui ne dépend que du point final considéré, ce qui simplifie les calculs.

Le vecteur est appelé vecteur de diffraction.

Comme l'extrémité des vecteurs est sur la sphère de centre O et de rayon k, l'extrémité des vecteurs est sur la sphère dont le centre est la translation de l'origine par , et de rayon k.

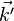
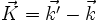
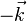
Association de réseaux

Association de deux réseaux sur un même plan

Il est possible d'associer les réseaux deux par deux ; les rayons doivent alors vérifier les deux conditions de diffraction, ce qui revient à prendre l'intersection des réseaux réciproques.

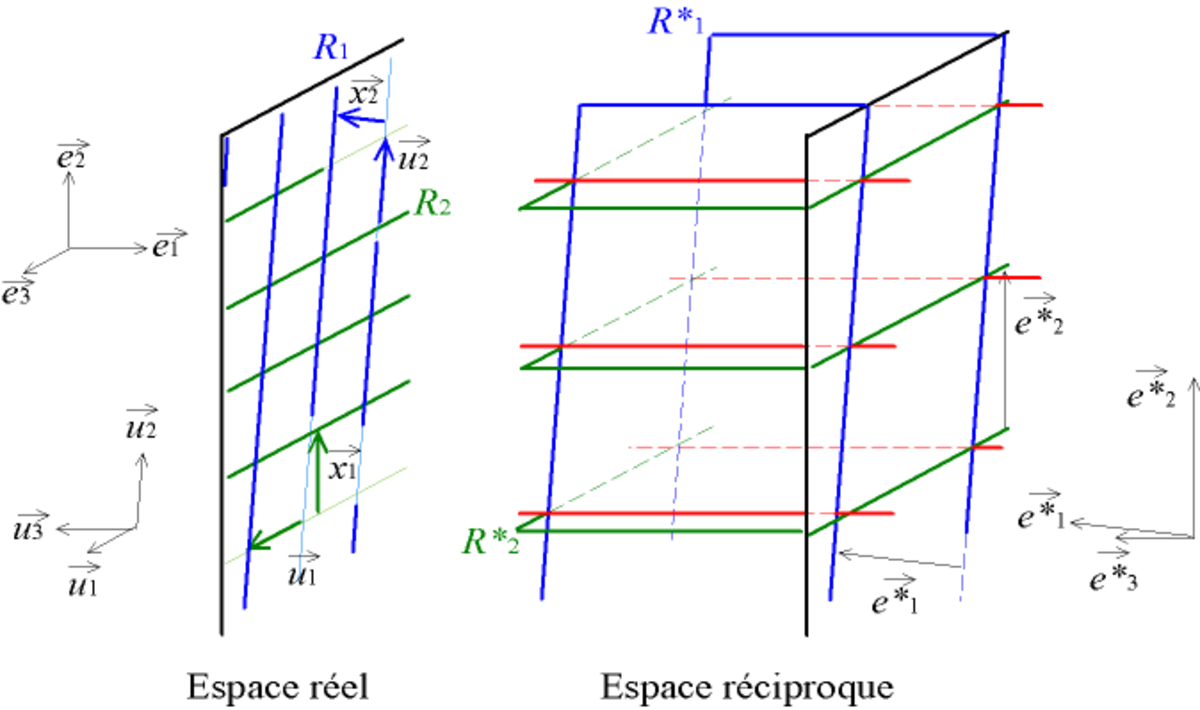
Prenons par exemple deux réseaux plans d'orientation différente, c'est-à-dire un quadrillage du plan . Les réseaux réciproques sont des plans perpendiculaires aux vecteurs de translation des réseaux. L'intersection entre deux plans non parallèles est une droite ; le réseau réciproque de ce quadrillage est donc une « forêt » de droites parallèles à .

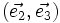
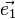
Pour un vecteur donné, les directions dans lesquelles se trouvent taches de diffraction sont déterminées par l'intersection entre la demi-sphère des et cette forêt de droites.

Appelons R₁ le premier réseau ; le vecteur de translation entre deux traits, normal aux traits, est noté , le vecteur directeur unitaire des traits est noté et le réseau réciproque de plans est noté R^*₁. Le second réseau est noté R₂, son vecteur de translation est , son vecteur directeur unitaire est est et le réseau réciproque est R^*₂. On note  ; le signe est choisi en fonction de l'orientation de et de afin que le trièdre soit direct ; on note que cette famille forme une base.

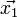
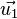
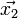
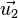
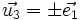
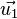
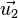
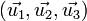
Les plans de R^*₁ sont perpendiculaires à et sont espacés de 2π/||x'₁||, ceux de R^*₂ sont perpendiculaires à et sont espacés de 2π/||x'₁||. Si l'on définit une nouvelle base

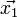
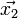
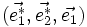
(l'inversion des indices est purement conventionnelle et est expliquée ci-après), alors dans cette base, les plans de R^*₂ ont pour équation

K_x = a, a étant un nombre entier

les plans de R^*₁ ont pour équation

K_y = b, b étant un nombre entier

et donc les droites représentant les conditions de diffraction ont pour équation

Dans la pratique, on se réfère plutôt aux vecteurs directeurs des traits des réseaux, et on définit

le vecteur n'a pas d'utilité pratique ici mais permet de définir de manière systématique une nouvelle base. L'inversion des indices est justifiée ici par une construction systématique de vecteurs de la base (permutation circulaire des indices).

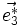
Maintenant, considérons que joint deux intersections de R₁ et de R₂, idem pour . Soit V le volume du parallélépipède formé par , et . On a :

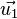
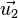
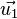
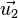
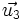
on a alors

Cette base est appelée base réciproque. Elle est caractéristique des réseaux.

Réseaux sur des plans parallèles

On peut aussi prendre des plans parallèles pourtant toutes un réseau identique, par exemple des plaques transparentes avec un réseau de traits réfléchissants (argenté). On choisit de prendre les plans parallèles à , et les traites du réseau perpendiculaires à .

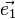
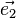
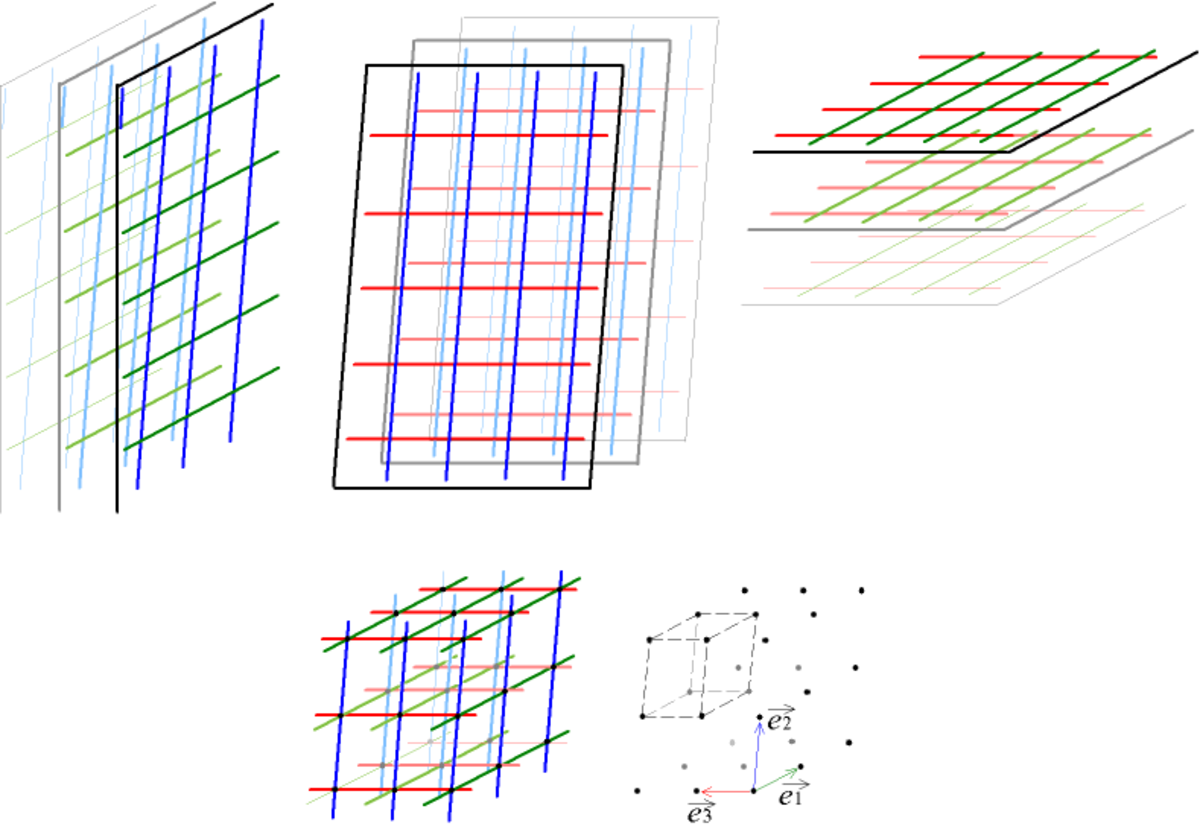
Le réseau réciproque de ce montage est alors l'intersection entre les plans de l'espace réciproque, perpendiculaires à , générés par la succession de plans réfléchissants, et les plans réciproques du réseau plan, perpendiculaires à . Le réseau réciproque de ce montage est donc une série de droites parallèles à .

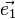
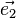
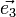
On peut enfin envisager une succession de plans parallèles portant tous un quadrillage identique. Le réseau réciproque est l'intersection de trois réseaux de plans ; c'est donc un réseau de points. On voit que l'on obtient le même réseau de points dans l'espace réciproque pour plusieurs configurations dans l'espace réel, à partir du moment où les intersections des traits se trouvent au même endroit. Ce qui définit les directions dans lesquelles l'intensité est non nulle, ce sont les vecteurs , et définissant la maille élémentaire.

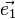
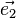
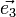
On peut définir comme précédemment les vecteurs , et de l'espace réciproque

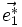
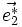
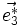
où (i, j, k) est une permutation circulaire de (1, 2, 3). Les vecteurs de diffraction pour lesquels il y a diffraction vérifient

où a, b et c sont des entiers. Le réseau réciproque est donc un réseau de points, les vecteurs , et définissant une maille élémentaire de ce réseau réciproque.

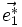
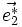
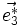
Base réelle et base réciproque

D'après les propriétés du produit vectoriel, on a :

, soit et

, soit et

, soit et

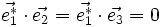
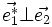
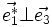
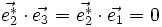
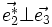
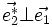
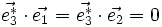
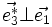
Par ailleurs, si (i, j, k) est une permutation circulaire de (1, 2, 3), on a :