Extension séparable - Définition

Introduction

Une extension algébrique L d'un corps K est dite séparable si et seulement si le polynôme minimal de tout élément de L n'admet que des racines simples.

Ce critère est une hypothèse nécessaire pour établir un théorème important de la théorie de Galois: Le théorème de l'élément primitif. La séparabilité est aussi utilisée dans la définition d'une extension de Galois.

Les corps dont toutes les extensions algébriques sont séparables sont nombreux. On y trouve par exemple les corps de caractéristique nulle, ce qui recouvre les nombres rationnels, les nombres réels et les nombres complexes.

Motivation

Le groupe des automorphismes de corps est un puissant outil d'analyse d'une extension algébrique. Il est particulièrement efficace si le nombre de racines du polynôme minimal est toujours égal à son degré. Cette propriété est toujours vérifiée si le corps initial est de caractéristique nulle ou si le corps est fini. On parle alors du Groupe de Galois. En revanche, cette propriété n'est pas vraie sur tous les corps, la théorie de Galois qui est l'étude des extensions algébriques demande pour la démonstration de l'essentiel des théorèmes la séparabilité.

La première conséquence de la séparabilité est le théorème de l'élément primitif. Si une extension finie L sur un corps K est séparable alors il existe un élément l de L de polynôme minimal P(X) sur K tel que L soit le plus petit corps de rupture de P(X). Cela signifie que L est égal à K(l) ou encore que L est une extension simple.

Dans le cas ou l'extension est finie et séparable, alors il existe autant d'automorphismes que la dimension de l'extension. Si ses automorphismes laissent stable l'extension, on parle alors d'Extension de Galois. C'est le contexte initial et le la théorie de Galois. Il existe alors une bijection entre les sous-corps de l'extension et les sous-groupes du groupe de Galois. L'étude de ces sous-groupes permet par exemple de déterminer une condition nécessaire et suffisante pour la résolubilité par radicaux d'une équation polynomiale.

Critères de séparabilité

Cas des polynômes

L'analyse de la séparabilité d'une extension revient à l'analyse des propriétés des polynômes sur K. En effet, pour qu'une extension soit séparable il faut et il suffit que ses éléments le soient, ce qui signifie que leurs polynômes minimaux le sont aussi. Il apparaît alors nécessaire d'établir des critères de séparabilité d'un polynôme. Il en existe un particulièrement simple.

• Un polynôme est séparable si et seulement si lui et sa dérivée formelle sont premiers entre eux.

Dans le cas d'un polynôme irréductible, particulièrement intéressant dans le cadre de la théorie de Galois, cette proposition implique le corollaire suivant :

• Un polynôme irréductible est séparable si et seulement si sa dérivée formelle n'est pas nulle.

Ce corollaire permet de résoudre simplement le cas des corps de caractéristique nulle. En particulier, les trois corps les plus usuels, les nombres rationnels, les nombres réels et les nombres complexes sont des corps parfaits. Il existe néanmoins un critère de séparabilité d'un polynôme irréductible.

• Supposons K de caractéristique p et P(X) un polynôme irréductible. Il est séparable si et seulement s'il n'existe pas de polynôme Q[X] dans K[X] tel que l'on ait l'égalité P(X)=Q(X^p).

• Un polynôme P(X) élément de K[X] est séparable si et seulement si lui et sa dérivée formelle sont premiers entre eux.

Dire de P(X) n'est pas séparable revient à dire que ce polynôme s'écrit dans Ω[X] de la manière suivante (X-a)ⁿQ[X], ou a est un élément de Ω et n un entier supérieur ou égal à deux. Alors la dérivée formelle de P(X) vérifie l'égalité suivante:

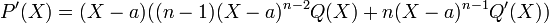
P(X) et P'(X) sont deux polynômes de K[X] qui ne sont pas premiers entre eux dans Ω[X], ils ne sont donc pas premiers entre eux dans K[X]. Et la proposition est démontrée.

• Un polynôme irréductible est séparable si et seulement si sa dérivée formelle n'est pas nulle.

C'est un corollaire direct de la proposition précédente. Le seul polynôme de degré strictement inférieur à P(X) annulant a, une racine dans Ω de P(X) est le polynôme nul.

• Supposons K de caractéristique p et P(X) un polynôme irréductible. Il est séparable si et seulement s'il n'existe pas de polynôme Q(X) dans K[X] tel que l'on ait l'égalité P(X)=Q(X^p).

Si le polynôme Q(X) existe avec la propriété de l'énoncée, alors la dérivée de P(X) vérifie l'égalité suivante:

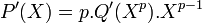
Comme le K est de caractéristique p, le polynôme dérivé est nul et la proposition précédente permet de conclure. Réciproquement si un tel polynôme n'existe pas, notons alors a_i les coefficients du polynôme P(X). Alors la dérivée vérifie l'égalité suivante:

Comme P(X) n'est pas un polynôme en X^p il existe un coefficient a_i qui n'est pas multiple de p avec i non plus car p est premier puisque K est un corps. Ce qui montre que la dérivée formelle de P(X) n'est pas nulle.

 

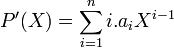
Cas des extensions et des corps

Ce paragraphe précédent permet de résoudre simplement le cas des corps de caractéristique nulle.En particulier, les trois corps les plus usuels, les nombres rationnels, les nombres réels et les nombres complexes sont des corps parfaits.

• Si un corps est de caractéristique nulle, alors il est parfait.

Ce ne sont néanmoins pas les uniques cas où une extension est séparable. La proposition suivante donne un exemple de séparabilité indépendamment de la caractéristique:

• Soit L une extension de K et M une extension de L. Alors si M est une extension séparable de K, alors M est séparable sur L et L est séparable sur K.

Dans le cas où la caractéristique de K est égale à p, alors K est parfait si et seulement si tout élément de K possède une racine pième. On en déduit que:

• Tout corps fini est parfait.

Ces propriétés sont démontrées dans l'article détaillé.