Extension séparable - Définition
La liste des auteurs de cet article est disponible ici.
Définitions et premiers exemples
Dans la suite de l'article, K désigne un corps, L une extension algébrique, P(X) un polynôme formel à coefficients dans K et scindé sur L et l un élément de L. Ω désigne la clôture algébrique de K, dans cet article, toute extension est identifiée à un sous-corps de Ω. Cette identification est licite, d'après le paragraphe sur la clôture algébrique.
-
- l est séparable dans K si et seulement si son polynôme minimal est séparable.
-
- L est séparable dans K si et seulement si tous ses éléments le sont.
-
- K est un corps parfait si et seulement si toutes ses extensions algébriques sont séparables.
Le polynôme X3-2 sur le corps des nombres rationnels est séparable. En effet, il possède trois racines, une réelle : la racine cubique de deux et deux complexes conjuguées entre elles. les trois racines sont distinctes. De manière générale sur les nombres rationnels, tout polynôme irréductible est séparable.
Cependant, tous les polynômes irréductibles ne sont pas séparables. Considérons Fp(X) le corps des fractions rationnelles sur le corps fini de cardinal p, où p est premier, et Ω sa clôture algébrique. Si K est choisi comme étant égal à l'ensemble des fractions de Fp(Xp), alors K contient un polynôme non séparable. Considérons le polynôme P(X) de K[Y] égal à Yp-Xp. Ce polynôme possède une unique racine X qui est donc un élément algébrique de degré p. De plus ce polynôme est irréductible. On en déduit que Fp(X) est le corps de décomposition du polynôme P(X). Comme X est sa seule racine, P(X) n'est pas séparable.
Propriétés
Morphisme dans la clôture algébrique
L'une des raisons essentielles de l'intérêt de la notion de séparabilité provient du nombre de morphisme de corps de L dans Ω laissant invariant K. Cette propriété est utilisée pour le théorème de l'élément primitif et pour de nombreuses propriétés des extensions galoisiennes. L'unique cas traité ici est celui ou L est une extension finie. Dans la suite de l'article, L est toujours supposé finie de dimension n. Le cas ou il existe un élément l générateur de l'extension est traité par la proposition suivante:
-
- S'il existe un élément l tel que K(l) est égal à L alors il existe au plus n morphismes de L dans Ω. Si l est séparable, alors il existe exactement n morphismes.
Dans le cas général, c’est-à-dire sans hypothèse de séparabilité ni de simplicité de l'extension, une propriété analogue est toujours vraie.
-
- Le nombre de morphismes de L dans Ω laissant invariant K est inférieur ou égal à n.s
Elle se démontre à l'aide de la propriété suivante:
-
- Soit une famille finie de m morphismes de L dans Ω. Si les morphismes sont distincts deux à deux, alors la famille est libre.
Dans le cas particulier où l'extension est engendrée par des éléments séparables, l'hypothèse de simplicité de l'extension n'est pas nécessaire pour obtenir un résultat analogue à la première proposition:
-
- Si L est engendré par des éléments séparables alors il existe exactement n morphismes de corps de L à valeur dans Ω laissant invariant K.
Pour la démonstration, les propositions suivantes sont utilisées :
-
- Si L est une extension finie de K1 et K1 une extension de K, alors un morphisme de K1 dans Ω laissant invariant K se prolonge en un morphisme de L dans Ω laissant invariant K.
- Si L est une extension de K1 contenant n1 morphismes de L dans Ω laissant invariant K1 et K1 une extension de K contenant n2 morphismes de K1 dans Ω laissant invariant K, alors il existe au moins n1.n2 morphismes de L dans Ω laissant invariant K.
-
- S'il existe un élément l tel que K(l) est égal à L alors il existe au plus n morphismes de L dans Ω laissant invariant K. Si l est séparable, alors il existe exactement n morphismes.
Soit P(X) le polynôme minimal de l dans K. La première proposition du paragraphe Extension algébrique et sur-corps indique, pour toute racine xi de P(X) dans Ω, l'existence d'un morphisme de L dans Ω qui à l associe xi. Il existe donc au moins autant de morphismes que de racines de P(X).
Réciproquement, si f est un morphisme de L dans Ω, alors P(f(l))=f(P(l)))=0. Donc l a pour image par f une racine.
En conclusion, il existe exactement autant de morphismes que de racines de P(X) dans Ω. Dans le cas général il n'existe donc jamais plus de morphismes que le degré de P(X), lequel est égal à la dimension de L. En effet, la famille (1, l, l2, ... , ln-1) est une base de L. Une condition nécessaire et suffisante d'égalité entre le nombre de morphismes et la dimension de L est la séparabilité de l.
-
- Soit une famille finie de m morphismes de L dans Ω. Si les morphismes sont distincts deux à deux, alors la famille est libre en tant que partie d'un espace vectoriel de corps Ω.
Raisonnons par contraposée. Soit (fi) une famille linéairement dépendante de m morphisme, à une permutation près, on peut supposer que l'élément d'indice p est non nul, et combinaison linéaire des précédents qui forment une famille libre. l'égalité suivante est donc vérifiée:
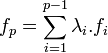
Si l et l' sont deux éléments de L tel que l' soit choisi non nul, alors fi(l.l')=fi(l)fi(l'). Comme fi(l') est non nul, l'égalité suivante est vérifiée:
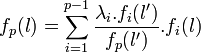
La famille des p-1 premiers éléments est choisie libre. La combinaison linéaire est unique, on en déduit les p-1 égalités suivantes.
![\forall i \in [1, p-1]\quad \lambda_i.f_i(l')=\lambda_i.f_p(l')\;](https://static.techno-science.net/illustration/Definitions/autres/7/77a88fe8e0b14aa40ab07e90cddd496f_3a48a40affa2ad9e15cc3ce88d530d74.png)
Cette égalité est vrai pour tout l' d'où l'égalité entre fi et c si le scalaire associé est non nul. Il existe au moins un scalaire associé non nul car fp est non nul. Nous avons démontré que la famille n'est pas distincte deux à deux. La contraposée permet de terminer la démonstration.
-
- Le nombre de morphismes de L dans Ω est inférieur ou égal à n.
Considérons E l'espace des applications K linéaires de L dans Ω. E est un espace vectoriel de dimension n sur le corps Ω. En effet, si (li) est une base de L l'application φ de E dans Ωn qui à une application linéaire m associe ((m(li)) est un isomorphisme d'espace vectoriel.
Considérons alors la famille de tous les morphismes de corps de L dans Ω. C'est une famille de E d'éléments distincts deux à deux. C'est donc une famille libre qui ne peut comporter plus d'éléments que la dimension de l'espace E. Et la proposition est démontrée.
-
- Si L est une extension finie de K1 et K1 une extension de K. Alors un morphisme f de K1 dans Ω laissant invariant K se prolonge en un morphisme de L dans Ω laissant invariant K.
L est un espace vectoriel sur K1 il existe donc une base (l1, l2, ...,lm) où l1 = 1 de L sur K1.
Considérons alors l'application g de L dans Ω défini par l'application définie par:
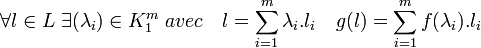
Montrons alors que g est un morphisme de L dans Ω. Pour cela considérons un deuxième élément l' de coordonnées λi' dans la base considérée:
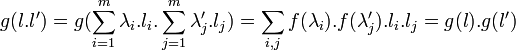
Les égalités précédentes montrent que g est le morphisme cherché et la proposition est démontrée car le corps K est manifestement invariant.
-
- Si L est une extension de K1 contenant n1 morphismes de L dans Ω laissant invariant K1 et K1 une extension de K contenant n2 morphismes de K1 dans Ω laissant invariant K. Alors il existe au moins n1.n2 morphismes de L dans Ω laissant invariant K.
La proposition précédente montre qu'il est possible d'étendre les morphismes de K1 à L. Il existe n1.n2 compositions différentes de morphismes. Il ne reste donc qu'à vérifier que ces morphismes sont tous distincts. Soit (mi) les n1 prolongements dans L des morphismes de K1 et (m'j) les n2 morphismes de L. Si mi est différent de mi' alors leurs composées avec des morphismes de la deuxième famille sont distinctes car elles sont distinctes sur K1.
Il suffit alors de montrer que les composés de mi avec deux morphismes différents m'j et m'j' sont distinctes. Si leurs images sont différentes, alors les composées sont distinctes car elles n'ont pas le même ensemble d'arrivée. Considérons le cas ou les images sont les mêmes. Alors la base de L de la proposition précédente a pour image par m'j une base B' de l'ensemble d'arrivée de m'j et m'j'. Soit l un élément de L ayant deux images différentes par m'j et m'j'. Il existe alors un élément de la base B' tel que les coefficients a et a' des images par les deux morphismes sont différents. D'après la construction de l'extension décrite durant la démonstration précédente, les coefficients des composées sont alors mi(a) et mi(a') qui sont différents car mi est injectif comme tous les morphismes de corps. Et la proposition est démontrée.
-
- Si L est engendré par des éléments séparables alors il existe exactement n morphismes de corps de L à valeur dans Ω laissant invariant K.
Montrons la proposition suivante par récurrence sur m:
Si une extension finie L d'un corps Ki est générée par m éléments de L, alors le nombre de morphismes de L dans Ω laissant invariant Ki au moins égal à la dimension de L sur Ki.
Si m est égal à 0, la proposition est trivialement vraie. Supposons le résultat vrai pour m est supposons que L est généré par une famille (li) de m+1 éléments. Notons alors K1 l'extension de K K(lm+1). L est alors une extension de K(lm+1) générée par m éléments séparables. L est une extension de K(lm+1) générée par m éléments, l'hypothèse de récurrence montre qu'il existe au moins la dimension de L sur K(lm+1) (que l'on note [L:K(lm+1)]) morphismes de L dans Ω laissant invariant K(lm+1). Nous avons démontré qu'il existe [K(lm+1):K] morphismes de K(lm+1) dans Ω laissant invariant K. La proposition précédente montre donc qu'ils existes au moins [L:K(lm+1)].[K(lm+1):K] morphismes de L dans Ω laissant invariant K. Or ce produit est égal à la [L:K] d'après une proposition élémentaire démontrée dans l'article Extension algébrique.
Donc si L est séparable, il existe au moins n morphismes. Or une proposition précédente montre qu'il en existe dans le cas général au plus n. La démonstration est donc terminée.Théorème de l'élément primitif
Toutes les propriétés du paragraphe précédent peuvent se résumer par le fait que, dans le contexte des extensions finies L sur K, la séparabilité implique que le nombre de morphismes est égal à la dimension de L sur K. Une analyse plus fine montre que les deux propriétés sont équivalentes. Ces deux propriétés sont aussi équivalente à une troisième: l'extension est engendrée par un unique élément séparable. Ainsi, pour une famille importante de corps, celle des corps parfaits contenant non seulement les corps usuels mais aussi tous les corps finis, toute extension finie est non seulement séparable, mais il existe autant de morphismes que la dimension de l'extension et l'extension est simple. Ce résultat se résume dans par un théorème fondamental pour la théorie de Galois, connu sous le nom de l'élément primitif.
-
- Les quatre conditions suivantes sont équivalentes:
- L'extension L est séparable sur K.
- L'extension est engendrée par des éléments séparables.
- Il existe exactement n morphismes de L dans Ω laissant invariant K.
- L est une extension simple générée par un élément séparable.
La démonstration est donnée dans l'article détaillé.
Forme trace
Il existe un critère nécessaire et suffisant pour qu'une extension finie soit séparable, elle utilise la forme trace, une forme bilinéaire de L. Soit φ l'application qui à a associe l'endomorphisme φa défini par :
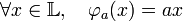
La forme trace associe à deux éléments a et b de L la trace de l'endomorphisme φab.
-
- L'extension L est séparable sur K si et seulement si la forme trace est non dégénérée.
La démonstration est donnée dans l'article détaillé.