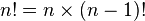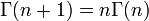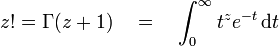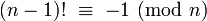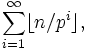Factorielle - Définition

Généralisation

La fonction gamma, tracée ici le long de l'axe des réels, prolonge la factorielle sur les valeurs qui ne sont pas entières

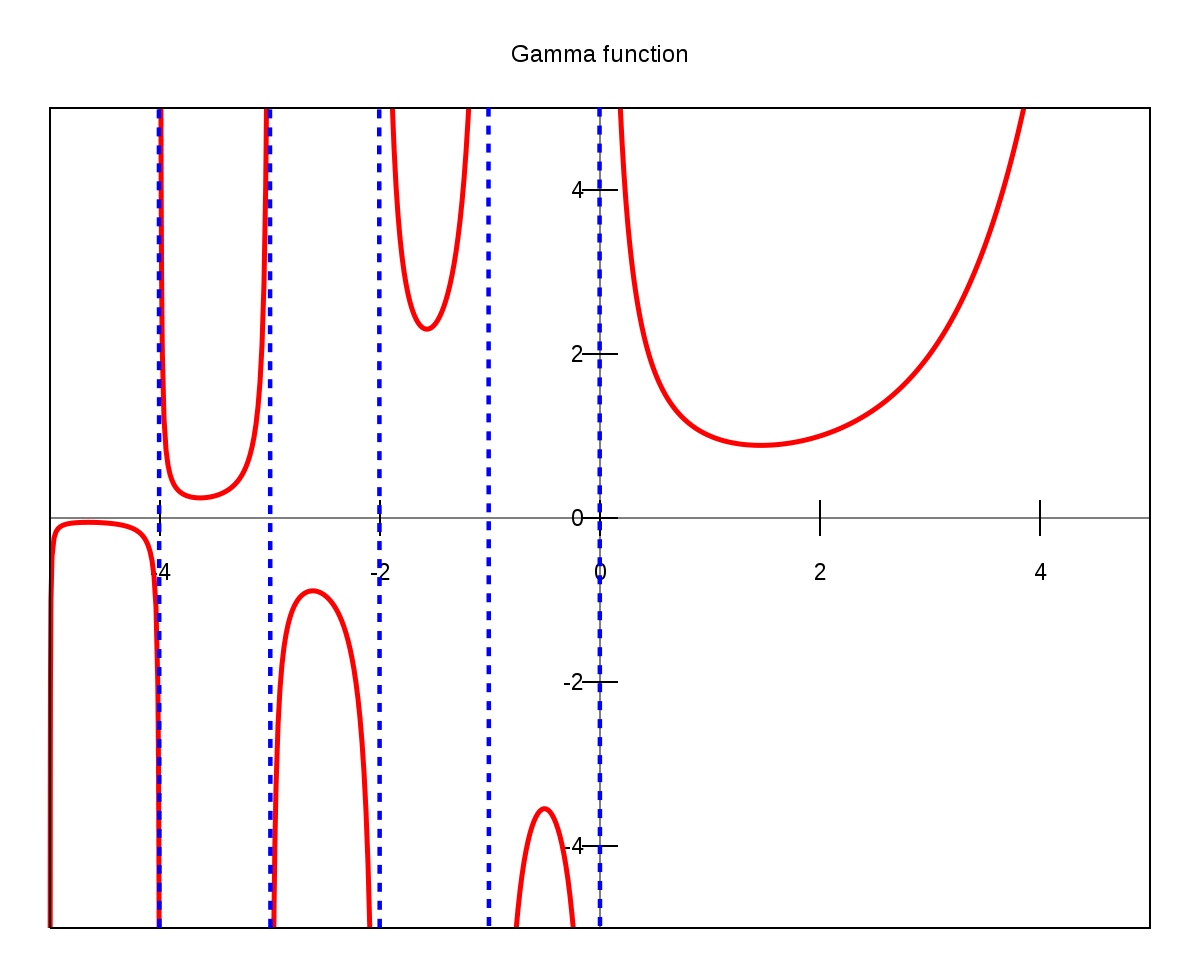
La fonction factorielle peut être prolongée à l'ensemble des nombres complexes (à l'exception des nombres entiers négatifs ou nuls) grâce à la fonction gamma d'Euler (notée Γ). En effet, pour n entier positif, on a :

Γ(n + 1) = n!

Par ailleurs, les deux fonctions satisfont les relations de récurrence suivantes :

La fonction gamma agit donc comme un prolongement de la factorielle :

Cette fonction n'est cependant pas définie pour les nombres entiers négatifs ou nuls (0, -1, -2, etc.).

Cette vision de la fonction gamma comme prolongation de la factorielle est justifiée par les raisons suivantes :

• les deux fonctions partagent une même définition récurrente ;
• la fonction gamma est généralement utilisée dans un contexte similaire (même si plus général) à la factorielle ;
• la fonction gamma est la seule fonction qui satisfait cette définition de récurrence sur les nombres complexes, qui est holomorphe et dont le logarithme de la restriction aux réels positifs est convexe (théorème de Bohr-Mollerup).

Variantes

De nombreux auteurs ont défini des fonctions analogues, croissant plus rapidement encore, ainsi que des produits restreints à certains entiers seulement. On rencontre ainsi dans la littérature les fonctions primorielles, multifactorielles, superfactorielles, hyperfactorielles, etc. Mais il ne semble pas que, contrairement à la factorielle, omniprésente dans la plupart des branches des mathématiques, ces autres fonctions aient eu beaucoup d'applications autres que récréatives ; quant à leur utilisation pour désigner de très grands nombres, les notations de Knuth et celles de Conway s'avèrent à la fois plus maniables et beaucoup plus efficaces.

Théorie des nombres

Les factorielles ont de nombreuses applications en théorie des nombres. Les nombres factoriels sont des nombres hautement composés. En particulier, n! est divisible par tous les nombres premiers qui lui sont égaux ou inférieurs. Par conséquent, tout nombre n > 4 est un nombre composé si et seulement si :

.

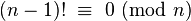
Un résultat plus fort est le théorème de Wilson. n est premier si et seulement si :

Adrien-Marie Legendre a montré que la multiplicité du nombre premier p dans la décomposition en produit de facteurs premiers de n! peut être exprimé par :

(qui est définie, car la fonction partie entière élimine tous les pⁱ > n).

La seule factorielle qui soit également un nombre premier est 2, mais il existe des nombres premiers de la forme , appelés nombres premiers factoriels.

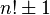
Implémentations

Le calcul de la factorielle peut se traduire par le programme suivant en pseudo-code (proche de C, C++, Java, Python, ...) :

factorielle(entier k) :

si k=0

alors renvoyer 1

sinon renvoyer k * factorielle(k-1)

finsi

qui donnerait en C :

      int factorielle(int n)      {          if(n==0)              return 1;          else              return n * factorielle(n - 1);      }      

en Pascal :

      function factorielle(n : integer):integer;      begin         if n = 0 then factorielle := 1         else factorielle := n * factorielle(n - 1);      end;      

en Caml :

      let rec factorielle = function        0 → 1      | n → n * factorielle (n-1);;      

en Prolog :

      factorielle(0,1).      factorielle(N,F):- M is N-1, factorielle(M,R), F is R*N.      

Notons que les algorithmes ci-dessus ne prennent pas en compte le fait que le factoriel croit de manière exponentielle et dépasse rapidement la capacité de stockage des "int 32 bits", "int 64 bits" ou même "int 128 bits". Seules les implémentations permettant un calcul en précision infini permettra le calcul effectif de la factorielle.