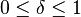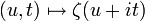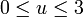Fonction zêta de Riemann - Définition
La liste des auteurs de cet article est disponible ici.
Représentation sous forme de produit de facteurs primaires
D'après le théorème de factorisation de Hadamard pour une fonction méromorphe, toute fonction méromorphe s'écrit sous forme de produit de facteurs dits primaires dans lesquels apparaissent les zéros et les pôles de la fonction. La représentation sous cette forme pour

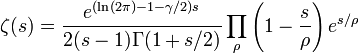
où le produit s'effectue sur les zéros ρ de

Que devient la série de Dirichlet sur l'axe Re(s) = 1 ?
La théorie des séries de Dirichlet montre, par le lemme d'Abel, que si la série converge en un point s0, elle converge pour tout s pour lequel  . Le domaine de convergence est donc un demi-plan. Pour la série de Riemann, la série converge sur le demi-plan
. Le domaine de convergence est donc un demi-plan. Pour la série de Riemann, la série converge sur le demi-plan 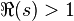 par suite du pôle en 1 (théorème de Dirichlet).
par suite du pôle en 1 (théorème de Dirichlet).
La série de Dirichlet converge-t-elle en dehors de 1, sur
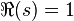
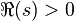 )
)
![\zeta(s)=\sum_{n=1}^N\frac1{n^s}+s\int_N^\infty{\frac{[u]-u+1/2}{u^{s+1}}}\mathrm du + \frac{N^{1-s}}{s-1}-\frac12 N^{-s}\,\!](https://static.techno-science.net/illustration/Definitions/autres/3/36eac9b4b9667546404484259a364001_2403a092bb00f64c4ee4bc2a62938fcd.png)
L'intégrale est O(t / σNσ) et le dernier terme se majore par O(N − σ). Ces deux termes tendent donc vers 0 quand N tend vers l'infini. Pour l'avant-dernier terme on a
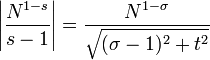
et il en résulte que lorsque N tend vers l'infini, ce terme prend des oscillations de plus en plus importantes si 0 < σ < 1: la série de Dirichlet diverge. Pour s = 1 + it, le terme devient
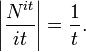
Il ne tend pas vers 0: la série diverge mais ses oscillations restent bornées par 1 / t.
Pour les séries de Dirichlet de
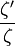
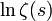
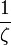
Représentation de et fonction M de Mertens
La fonction
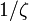

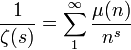
L'application de la formule sommatoire d'Abel donne également
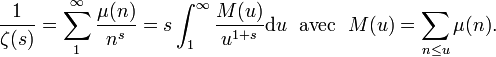
Cette formule est valable pour 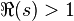 . On conjecture (hypothèse de Riemann) qu'elle reste vraie pour
. On conjecture (hypothèse de Riemann) qu'elle reste vraie pour  . On sait qu'elle est également valable pour s = 1 + it,
. On sait qu'elle est également valable pour s = 1 + it,
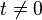
La théorie de M est très obscure et cela probablement pour longtemps. On ne sait que démontrer l'estimation suivante:
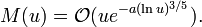
La relation fonctionnelle approchée
Comme on a vu dans la partie , il est possible de calculer la fonction

Pour 0 < σ < 1 et 2πxy = t avec x > h > 0, y > h > 0, on a
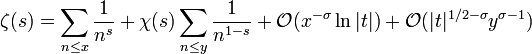
avec
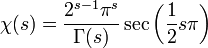
On peut, avec elle, obtenir une première estimation de
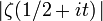
Estimation de la fonction dans les diverses régions du plan
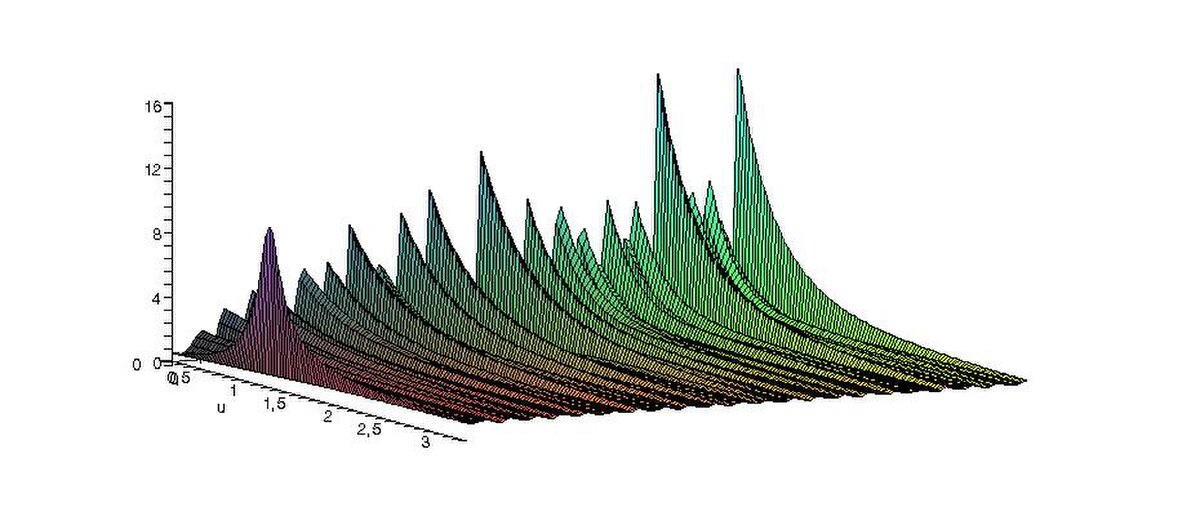
Presque périodicité
La fonction

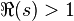 . Il en est de même de ses dérivées. La fonction
. Il en est de même de ses dérivées. La fonction
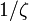
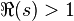 ainsi que ses dérivées. Par contre sur l'axe 1, la presque périodicité de Bohr cède sa place à la presque périodicité B2, au sens de Besicovitch.
ainsi que ses dérivées. Par contre sur l'axe 1, la presque périodicité de Bohr cède sa place à la presque périodicité B2, au sens de Besicovitch.
La presque périodicité au sens de Bohr, sur la ligne
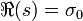


Estimations dans la région Re(s) > 1
Dans le demi-plan  la fonction
la fonction
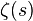
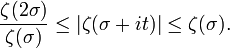
Elle n'a donc aucun zéro dans le demi-plan  .
.
Ces deux bornes sont les meilleures possibles: on montre, pour chaque valeur, qu'il existe une suite de t tendant vers l'infini ayant cette valeurs pour limite de la suite ζ(σ + it).
Charles-Jean de La Vallée Poussin démontra que pour σ > 1, on a
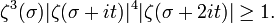
Une estimation, souvent utile, est donnée par la formule suivante pour les valeurs réelles de s supérieures à 1
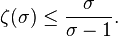
Elle résulte de la formule issue de la formule sommatoire d'Abel déjà donnée en remarquant que l'intégrale est toujours positive et affectée du signe -.
Estimations sur Re(s) = 1
La fonction

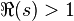 . Elle y est donc bornée sur tout demi-plan fermé strictement inclus. La présence du pôle en 1 empêche toute extension de la presque périodicité au sens de Bohr à un demi-plan plus vaste. Il est donc important de connaître le comportement de la fonction sur l'axe 1.
. Elle y est donc bornée sur tout demi-plan fermé strictement inclus. La présence du pôle en 1 empêche toute extension de la presque périodicité au sens de Bohr à un demi-plan plus vaste. Il est donc important de connaître le comportement de la fonction sur l'axe 1.
La méthode de Vinogradov-Korobov sur les majorations des sommes d'exponentielles permet de montrer que l'on a, pour tout t, l'inégalité
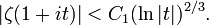
On connait, sans aucune hypothèse, une minoration de l'ordre des fonctions ζ(1 + it) et 1 / ζ(1 + it). On a en effet (γ = 0,577... est la constante d'Euler—Mascheroni)
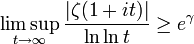
et
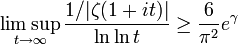
La fonction n'est donc pas bornée sur l'axe 1, même en dehors du voisinage de 1.
Estimations sur Re(s) = 0
Utilisant la formule des compléments et la relation fonctionnelle, on trouve pour t non nul
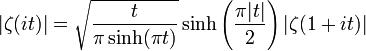
et de ce fait
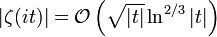
Estimations dans la région Re(s) < 0
L'application de l'équation fonctionnelle et de la formule de Stirling, et le comportement asymptotique de sin(σ + it) permet de montrer que
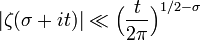
pour σ < 0.
Estimation dans la bande critique
On peut estimer, uniformément dans la bande critique,
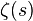
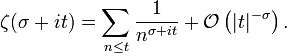
De la méthode de Vinogradov-Korobov on déduit la majoration suivante : il existe deux constantes c et C strictement positives telles que pour tout
![\sigma \in [1/2,1]](https://static.techno-science.net/illustration/Definitions/autres/8/8a71bf29d1634f9adff445de13b91244_e3cfa79330e1455315e627b1f394bdc1.png)
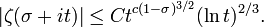
Dans l'état actuel des connaissances, d'après Ford, on peut prendre C = 76,2 et c = 4,45. La relation fonctionnelle permet d'estimer le module dans la bande
![\sigma \in [0,1/2].](https://static.techno-science.net/illustration/Definitions/autres/d/d4411363bb7029e77f958a2efeba3a72_05df063b4e240cc20715d26f9bfd48e0.png)
Le théorème de Valiron
Quand on regarde les applications arithmétiques de la fonction

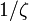
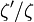
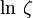

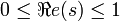
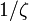
Dans sa thèse soutenue en 1914, Georges Valiron a montré qu'il existait une infinité de valeurs de t dans tout intervalle [T,T + 1] pour lesquelles on avait la minoration
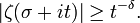
pour un certain δ fixe strictement positif.
On ne connaît aucune valeur de δ qui convient. On sait seulement que