Jeudi 19 Juin 2025
Rechercher 🔍

Fonction zêta de Riemann - Définition

Source: Wikipédia sous licence CC-BY-SA 3.0.
La liste des auteurs de cet article est disponible ici.
- Introduction - Prologue - Valeurs de la fonction zêta pour s entier supérieur à 1 - Définition par la série de Dirichlet - Extension à ℂ-{1} - Liens avec les nombres premiers - Relation fonctionnelle et zéros triviaux de la fonction zêta - Le comportement au voisinage de 1 : théorème de Dirichlet et nombres de Stieltjes - Définition de ln ζ et de sa dérivée - Représentation sous forme de produit de facteurs primaires - Que devient la série de Dirichlet sur l'axe Re(s) = 1 ? - Représentation de et fonction M de Mertens - La relation fonctionnelle approchée - Estimation de la fonction dans les diverses régions du plan - Les grandes conjectures - Les zéros - Applications diverses - Le problème des moments

Valeurs de la fonction zêta pour s entier supérieur à 1

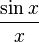
Euler a calculé (dans le cadre de sa solution au problème de Bâle) la valeur de la fonction \zeta\, pour les entiers positifs pairs en utilisant l'expression de \sin x\over x sous forme de produit infini ; il en a déduit la formule :

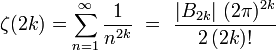
\zeta(2k)=\sum_{n=1}^{\infty}\frac1{n^{2k}} \ = \ \frac{|B_{2k}| \ (2\pi)^{2k}} {2 \, (2k)!}

valable pour tout entier positif k, où les B2k sont les nombres de Bernoulli. De là, nous obtenons des séries infinies correspondant aux puissances paires de π :

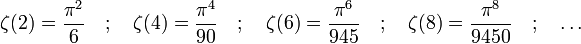
\zeta(2) = \frac{\pi^2}{6} \quad ; \quad \zeta(4) = \frac{\pi^4}{90} \quad ; \quad \zeta(6) = \frac{\pi^6}{945}\quad ; \quad \zeta(8) = \frac{\pi^8}{9450} \quad ; \quad \dots

Pour les entiers impairs, le calcul n'est pas si simple. Ramanujan a beaucoup travaillé sur ces séries et Apéry a démontré en 1979 que ζ(3), qui vaut environ 1,2020569... est irrationnel (voir constante d'Apéry). En 2000, Tanguy Rivoal a démontré qu'il existe une infinité de nombres irrationnels parmi les valeurs aux entiers impairs. On conjecture que toutes les valeurs aux entiers impairs sont irrationnelles et même transcendantes.

Définition par la série de Dirichlet

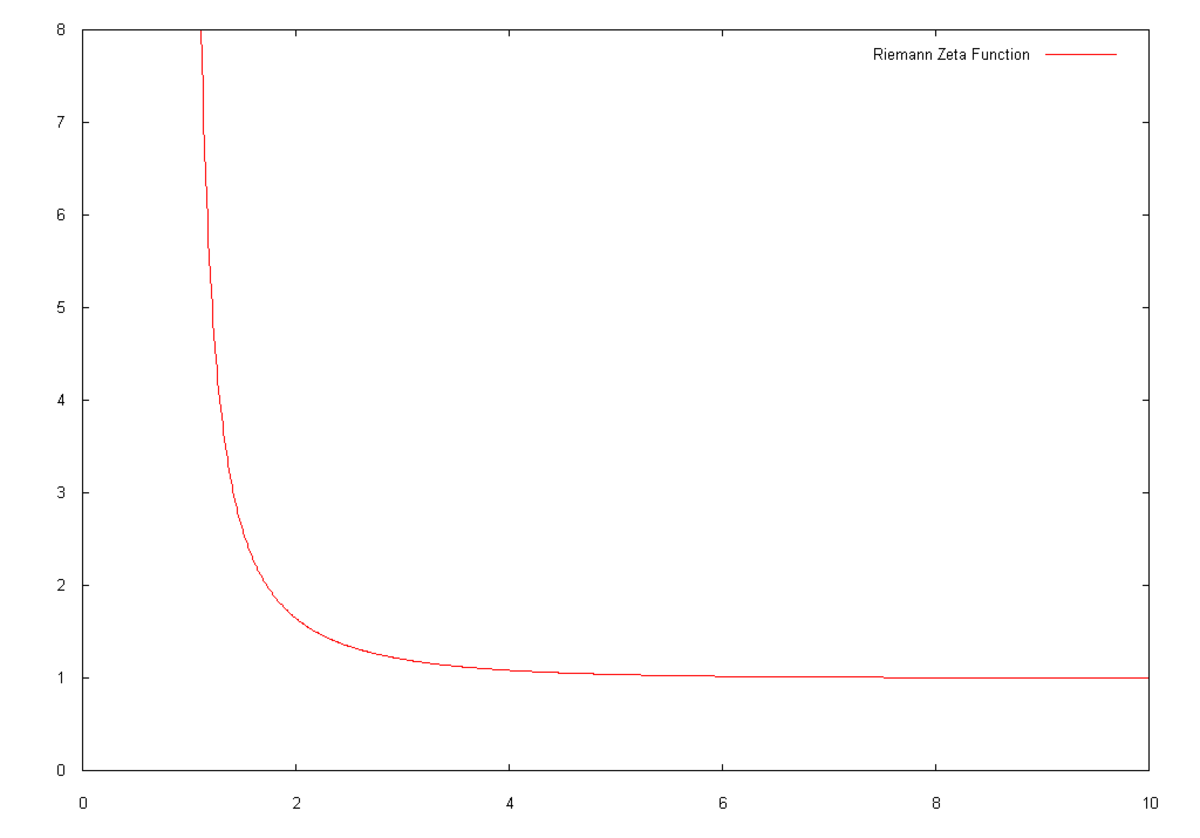
La fonction zêta de Riemann pour les réels s > 1

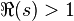La fonction \zeta\, de Riemann est une fonction analytique complexe méromorphe et définie, pour \Re(s)>1, par la série de Dirichlet

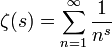
\zeta(s)=\sum_{n=1}^\infty{\frac1{n^s}} .

La série ne converge pas en s = 1 : on a

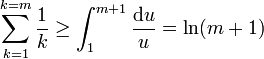
\sum_{k=1}^{k=m}\frac1{k}\ge \int_1^{m+1} \frac{\mathrm{d}u}{u}= \ln (m+1)\,\!

qui tend vers l'infini avec m (voir l'article détaillé série harmonique pour d'autres démonstrations de ce résultat, et une estimation plus précise de la valeur des sommes partielles). La valeur s = 1 est donc une singularité de la fonction.

À partir de la série de Dirichlet de \zeta\, on démontre les formules suivantes :

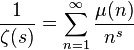
\frac{1}{\zeta(s)}=\sum_{n=1}^{\infty} \frac{\mu(n)}{n^s}

où μ est la fonction de Möbius,

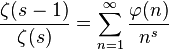
\frac{\zeta(s-1)}{\zeta(s)}=\sum_{n=1}^{\infty} \frac{\varphi(n)}{n^s}

où \varphi est l'indicatrice d'Euler, et

\zeta(s) \zeta(s-a)=\sum_{n=1}^{\infty} \frac{\sigma_{a}(n)}{n^s}
\frac{\zeta(s)\zeta(s-a)\zeta(s-b)\zeta(s-a-b)}{\zeta(2s-a-b)} =\sum_{n=1}^{\infty} \frac{\sigma_a(n)\sigma_b(n)}{n^s}

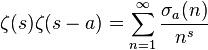
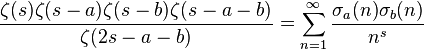
où σa est la fonction diviseur à la puissance a :

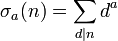
\sigma_a(n)= \sum_{d |n} d^a\,\!

Extension à ℂ-{1}

La fonction \zeta\, admet un prolongement analytique à tout le plan complexe, sauf 1. Il existe plusieurs démonstrations, faisant appel à différentes représentations de la fonction \zeta\, .

Par la formule d'Euler-Mac Laurin

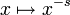
La formule d'Euler-MacLaurin, appliquée à la fonction x \mapsto x^{-s} sur l'intervalle [1 ; N], donne pour tout entier n :

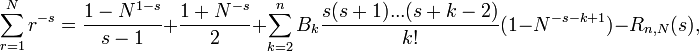
\sum_{r=1}^N r^{-s}={{1-N^{1-s}}\over {s-1}}+{{1+N^{-s}}\over {2}}+\sum_{k=2}^nB_k\frac{s(s+1)...(s+k-2)}{k!}(1-N^{-s-k+1}) -R_{n, N}(s),

où les coefficients Bk sont les nombres de Bernoulli,

R_{n, N}(s)={1\over {n!}}s(s+1)...(s+n-1)\int_1^N B_n(x-[x])x^{-s-n}\mathrm dx,\,\!

où les Bn(x) sont les polynômes de Bernoulli et où [x] désigne la partie entière de x.

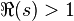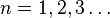
En faisant tendre N vers l'infini et en restant dans le demi-plan \Re(s)>1, on en déduit pour tout entier n=1, 2, 3\ldots que

\zeta(s)={{1}\over {s-1}}+{1\over {2}}+\sum_{k=2}^nB_k\frac{s(s+1)...(s+k-2)}{k!} -\frac{s(s+1)...(s+n-1)}{n!}\int_1^\infty B_n(x-[x])x^{-s-n}\mathrm dx.\,\!

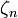
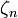
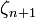
Les fonctions x \mapsto B_n(x-[x]) étant périodiques restent bornées sur l'intervalle d'intégration, donc l'intégrale à droite converge si \Re(s)>1-n. Donc le membre de droite définit une fonction, \zeta_n\, sur \Re(s)>1-n, holomorphe en dehors de 1, qui prolonge \zeta\, . L'unicité du prolongement analytique montre que les fonctions \zeta_n\, et sur \zeta_{n+1}\, sont identiques sur \Re(s)>1-n. Ces identités permettent donc de définir une unique fonction méromorphe sur tout le plan complexe (avec un seul pôle en 1), coïncidant avec la fonction 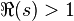\zeta\, déjà définie pour \Re(s)>1 et qu'on appelle encore \zeta\, .

Par une intégrale de contour

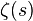
La fonction \zeta(s)\, se prolonge aussi analytiquement par l'intégrale

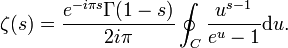
\zeta(s)=\frac{e^{-i\pi s}\Gamma(1-s)}{2i\pi}\oint_C{\frac{u^{s-1}}{e^u-1}\mathrm du}.

C désigne un lacet longeant l'axe réel et englobant 0 parcouru de +∞ à +∞ dans le sens trigonométrique.

Une fois cette formule démontrée initialement pour 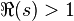\Re(s)>1, l'expression à droite restant valable pour tout valeur bornée de s définit donc une fonction analytique. D'après le théorème du prolongement analytique, elle représente le prolongement (sauf en s = 1) de la fonction \zeta\, .


Il est facile de démontrer que pour tout on a:

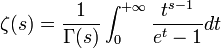
\zeta(s) = \frac{1}{\Gamma(s)} \int_{0}^{+ \infty} \frac{t^{s-1}}{e^t-1}dt \,\!

en effet:

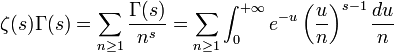
\zeta(s)\Gamma(s) = \sum_{n \geq 1} \frac{\Gamma(s)}{n^s} = \sum_{n \geq 1} \int_{0}^{+ \infty} e^{-u} \left( \frac{u}{n} \right)^{s-1} \frac{du}{n}\,\!

on pose u = nt alors:

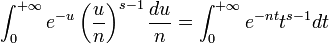
\int_{0}^{+ \infty} e^{-u} \left( \frac{u}{n} \right)^{s-1} \frac{du}{n} = \int_0^{+ \infty} e^{-nt}t^{s-1}dt\,\!

et d'après le Théorème de convergence monotone on peut intervertir somme-intégrale on a:

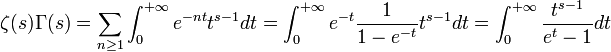
\zeta(s) \Gamma(s) = \sum_{n \geq 1} \int_{0}^{+ \infty} e^{-nt}t^{s-1}dt = \int_{0}^{+ \infty} e^{-t} \frac{1}{1-e^{-t}}t^{s-1}dt = \int_{0}^{+ \infty} \frac{t^{s-1}}{e^t-1}dt\,\!

enfin pour tout complexe s tel que on a:

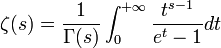
\zeta(s) = \frac{1}{\Gamma(s)} \int_0^{+ \infty} \frac{t^{s-1}}{e^t-1}dt\,\!


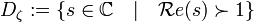
D'une autre part, on considère la fonction h sur l'ensemble D_{\zeta} := \{ s \in \mathbb{C} \quad | \quad \mathcal{R}e(s) \succ 1 \} par:

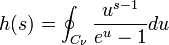
h(s) = \oint_{C_{\nu}} \frac{u^{s-1}}{e^u - 1} du

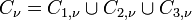
avec C_{\nu}= C_{1, \nu} \cup C_{2,\nu} \cup C_{3,\nu} le lacet décrit ainsi:

C1,ν: Demi-droite dont les points d'argument 0 décrite de + \infty à 0.

C2,ν : cercle de rayon ν et de centre 0, dont ces points croit de 0 à 2π.

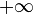
C3,ν: Demi-droite dont les points ont d'arguments 2π, décrite de ν à + \infty .

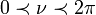
alors pour que h soit holomorphe sur tout le plan complexe on prend 0 \prec \nu \prec 2 \pi (voir que eu − 1 ne s'annule pas si ν est défini ainsi ) donc :

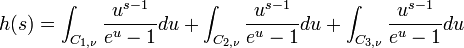
h(s) = \int_{C_{1, \nu}} \frac{u^{s-1}}{e^u - 1} du + \int_{C_{2, \nu}} \frac{u^{s-1}}{e^u-1}du + \int_{C_{3, \nu}} \frac{u^{s-1}}{e^u-1}du \,\!

d'une part il est clair que:

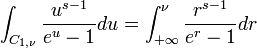
\int_{C_{1, \nu}} \frac{u^{s-1}}{e^{u}-1}du = \int_{+ \infty}^{\nu} \frac{r^{s-1}}{e^r-1}dr\,\!

alors:

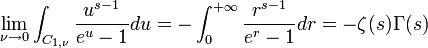
\lim_{ \nu \to 0} \int_{C_{1, \nu}} \frac{u^{s-1}}{e^u - 1 }du = - \int_{0}^{+ \infty} \frac{r^{s-1}}{e^r-1}dr = - \zeta(s)\Gamma(s) \,\!

et que:

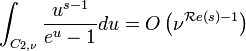
\int_{C_{2, \nu}} \frac{u^{s-1}}{e^{u}-1}du = O \left(\nu^{\mathcal{R}e(s)-1} \right)\,\!

ce qui entraine le fait que:

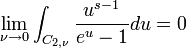
\lim_{ \nu \to 0} \int_{C_{2,\nu}} \frac{u^{s-1}}{e^u - 1 }du = 0\,\!

et enfin que:

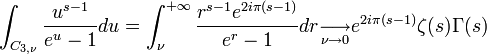
\int_{C_{3 ,\nu}} \frac{u^{s-1}}{e^u-1}du = \int_{\nu}^{+ \infty} \frac{r^{s-1} e^{2 i \pi (s-1)}}{e^r - 1 }dr \underset{\nu \to 0}{ \longrightarrow } e^{2 i \pi (s-1)} \zeta(s) \Gamma(s)\,\!

et puisque la fonction h est indépendante de ν alors:

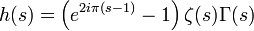
h(s) = \left( e^{2 i \pi (s-1)} - 1 \right) \zeta(s) \Gamma(s)

En utilisant les Formules d'Euler on trouve que :

e2iπ(s − 1) − 1 = 2isin(π(s − 1))eiπ(s − 1) = 2isin(πs)eiπs


alors en substituant l'expression on aura:

h(s) = 2ieiπssin(πs)ζ(s)Γ(s)

et d'une autre côté, d'après la formule des compléments de la fonction gamma, on a pour tout s tel que \Re{e}(s) \in ]0,1[

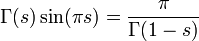
\Gamma(s) \sin ( \pi s) = \frac{\pi}{\Gamma(1-s)}

d'où:

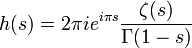
h(s) = 2 \pi i e^{i \pi s} \frac{\zeta(s)}{\Gamma(1-s)}

finalement:

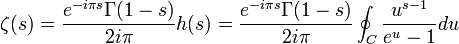
\zeta(s) = \frac{e^{-i \pi s} \Gamma(1-s)}{2 i \pi} h(s) = \frac{e^{-i \pi s} \Gamma(1-s)}{2 i \pi} \oint_{C} \frac{u^{s-1}}{e^u-1}du

et puisque h est holomorphe sur tout le plan ce qui implique le prolongement de la fonction ζ en fonction méromorphe dans \mathbb{C} .

 

Par la formule sommatoire d'Abel

Cette formule conduit à l'expression

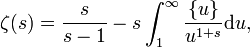
\zeta(s)=\frac{s}{s-1}-s\int_1^\infty{\frac{\{u\}}{u^{1+s}}\mathrm du},\,\!

où {u} désigne la partie fractionnaire de u. Comme {u} est toujours compris entre 0 et 1, l'intégrale est convergente pour 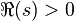\Re(s)>0.

Par la fonction êta de Dirichlet

On peut encore étendre la fonction 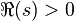\zeta\, sur \Re(s)>0 à partir de la définition de la série alternée (appelée fonction êta de Dirichlet)

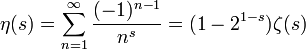
\eta(s)=\sum_{n=1}^\infty{\frac{(-1)^{n-1}}{n^s}}=(1-2^{1-s})\zeta(s)

Cette série est convergente pour s réel strictement positif, par application du critère des séries alternées ; il en est en fait de même pour 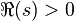\Re(s)>0, ce qui se démontre en utilisant le lemme d'Abel. Cela réalise ainsi le prolongement de la fonction 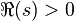\zeta\, sur \Re(s)>0. Le pôle en 1 de 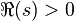\zeta\, est annulé par le terme (1 − 21 − s) ; on a η(1) = ln2. 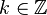À partir du prolongement pour \Re(s)>0 et en appliquant la relation fonctionnelle (voir plus loin), on obtient le prolongement partout sauf en 1 + 2ikπ / ln(2) ( k \in \mathbb{Z} ) qui sont les zéros de 1 − 21 − s.

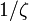
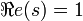
Pour ces points, on peut appliquer soit la série de Dirichlet de 1/\zeta\, , qui converge sur \Re{e}(s)=1 soit une autre relation du même genre.

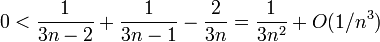
De ce que 0<\frac{1}{3n-2}+\frac{1}{3n-1}-\frac{2}{3n}=\frac{1}{3n^2}+O(1/n^3) , on déduit que la série

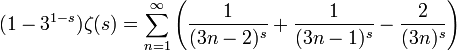
(1-3^{1-s})\zeta(s)=\sum_{n=1}^\infty{\left(\frac{1}{(3n-2)^s}+\frac{1}{(3n-1)^s}-\frac{2}{(3n)^s}\right)}

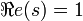
est convergente pour \Re{e}(s)=1 . Il suffit donc de calculer la série seulement pour ces points car ln3 / ln2 se trouvant irrationnel, le facteur (1 − 31 − s) ne peut être nul en même temps que celui de (1 − 21 − s).

Par la formule de Landau ou celle de Ramaswami

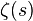
Dans les formules précédentes, il est à remarquer que le prolongement ne s'obtient que dans une portion du plan et qu'il faut utiliser la relation fonctionnelle pour avoir un prolongement au plan tout entier. Les deux formules qui suivent n'ont pas ce défaut. 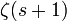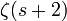Ces deux autres méthodes de prolongement de \zeta\, , sans conteste les plus simples, sont fondées, chacune, sur une formule exprimant \zeta(s)\, en fonction de \zeta(s+1)\, , \zeta(s+2)\, , ...

On a ainsi la formule publiée par Landau

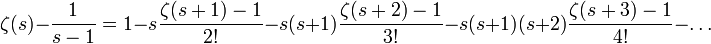
\zeta(s)-\frac1{s-1}=1-s\frac{\zeta(s+1)-1}{2!}-s(s+1)\frac{\zeta(s+2)-1}{3!}-s(s+1)(s+2)\frac{\zeta(s+3)-1}{4!}-\ldots

 

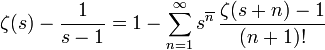
\zeta(s)-\frac1{s-1}=1-\sum_{n=1}^\infty s^{\overline{n}}\,\frac{\zeta(s+n)-1}{(n+1)!}\!

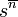
s^{\overline{n}} étant la factorielle croissante.

Ou la formule de Ramaswami

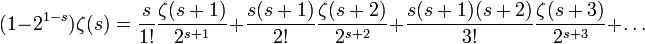
(1-2^{1-s})\zeta(s)=\frac{s}{1!}\frac{\zeta(s+1)}{2^{s+1}}+\frac{s(s+1)}{2!}\frac{\zeta(s+2)}{2^{s+2}}+\frac{s(s+1)(s+2)}{3!}\frac{\zeta(s+3)}{2^{s+3}}+\ldots

Ces formules se démontrent par des manipulations classiques sur les termes des séries.

Le prolongement analytique s'effectue par bandes de largeur 1. La série de Dirichlet étant absolument convergente sur 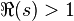\Re(s)>1, la formule choisie prolonge sur 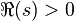\Re(s)>0. En appliquant à nouveau la formule, on prolonge à 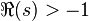\Re(s)>-1, et ainsi de suite.

Remarque: la présence du facteur 1 − 21 − s dans la formule de Ramaswami montre que le prolongement de \zeta\, par cette formule souffre du même problème que celui par la fonction η de Dirichlet.

Prologue
Liens avec les nombres premiers
- Introduction - Prologue - Valeurs de la fonction zêta pour s entier supérieur à 1 - Définition par la série de Dirichlet - Extension à ℂ-{1} - Liens avec les nombres premiers - Relation fonctionnelle et zéros triviaux de la fonction zêta - Le comportement au voisinage de 1 : théorème de Dirichlet et nombres de Stieltjes - Définition de ln ζ et de sa dérivée - Représentation sous forme de produit de facteurs primaires - Que devient la série de Dirichlet sur l'axe Re(s) = 1 ? - Représentation de et fonction M de Mertens - La relation fonctionnelle approchée - Estimation de la fonction dans les diverses régions du plan - Les grandes conjectures - Les zéros - Applications diverses - Le problème des moments
miniature
👽 Découvrir enfin une vie extraterrestre
miniature
🎯 Une piste très prometteuse pour empêcher les rechutes du cancer du sein
miniature
✨ Pourquoi les étoiles paraissent plus brillantes l'été ?
miniature
🌱 Comment les plantes résistent-elles à une lumière trop intense ?
miniature
2
⚫ Une IA révèle que le trou noir supermassif de notre galaxie pointe vers la Terre
miniature
🏔️ Découverte d'un monde perdu sous l'Antarctique
miniature
🌍 Découverte: cette règle universelle régit toute vie sur terre
miniature
⏳ L'Univers pourrait disparaître plus tôt que prévu: ce que révèle cette étude
miniature
🌍 Les dernières mesures révèlent un niveau de CO₂ jamais vu depuis 4 millions d'années
miniature
🛡️ Le paradoxe des gangs de rue
miniature
💰 Quelle quantité d'or existe-t-il vraiment sur Terre ?
miniature
🦟 Pourquoi les moustiques sont plus nombreux et piquent davantage en été ?
miniature
1
⚫ Ces trous noirs interagissent avec la lumière fossile du Big Bang
miniature
🦕 Et si les dinosaures détenaient le secret pour vaincre le cancer ?
miniature
😎 Comment font les lunettes de soleil pour filtrer les UV ?
miniature
🚶‍♂️‍➡️ La marche des babouins éclaire l'évolution de la bipédie humaine
miniature
🔭 James Webb capture cette image directe d'une étrange planète à 60 années-lumière
miniature
🦋 Pourquoi et comment les chenilles deviennent-elles des papillons ?
miniature
1
🔭 Voici la plus grande carte de l'Univers. Ses révélations sont surprenantes !
miniature
😴 Penser que l'on est éveillé alors que l'on dort, normal ?
miniature
🌊 Ce cratère raconte l'histoire de l'eau sur Mars
miniature
🐝 Comment les fleurs attirent-elles les insectes pollinisateurs ?
miniature
💥 La collision entre notre Voie lactée et la galaxie d'Andromède remise en question
miniature
🎶 Pourquoi les oiseaux chantent-ils autant et si fort au printemps ?
miniature
💡 Générer de la lumière à partir du vide, c'est possible
miniature
Découverte d'un deuxième système d'apprentissage dans le cerveau
miniature
☀️ Comment se produit un coup de chaleur et comment s'en protéger ?
miniature
⚽ Comment fonctionne la physique d'un tir puissant au foot ?
miniature
🧠 Un algorithme révèle comment notre cerveau se motive
miniature
🔭 Une si grande planète orbite une si petite étoile, comment est-ce possible ?
miniature
1
🐋 Les baleines développent de nouvelles méthodes pour communiquer avec nous
miniature
🥚 Le noyau de Mars sent l'œuf pourri
miniature
🧠 On sait enfin pourquoi le sémaglutide fait maigrir
miniature
🌱 La vie pourrait renaître sur Europe après la mort de la Terre
miniature
🌿 Confirmation scientifique: ce remède ancestral fait naturellement maigrir, et pas qu'un peu !
miniature
💥 Des astronomes identifient les plus puissantes explosions depuis le Big Bang
miniature
🦕 Ce crâne de stégosaure, le plus complet jamais découvert, réécrit l'histoire
miniature
🛏️ Les punaises de lit, ces compagnons indésirables depuis la préhistoire
miniature
🕸️ Connaissez-vous la toile cosmique, l'architecte de l'Univers ?
miniature
🌋 L'éruption de l'Etna vue depuis l'espace
miniature
🐋 Il y a 20 000 ans, l'Homme fabriquait des outils avec des os de baleines
miniature
🟠 Quel est le rôle de ce labyrinthe sur Mars ?
miniature
🎯 Cette stratégie innovante contre le cancer du sein offre une survie de 100%
miniature
1
💥 Le pulsar à trou noir: un objet qui intrigue les astrophysiciens
miniature
🐒 Première: ces singes kidnappent les bébés d'une autre espèce
miniature
🌍 Découverte d'une super-Terre à l'habitabilité intermittente
miniature
🧠 Ces cellules pourraient jouer un rôle bien plus important que les neurones dans la mémoire
miniature
🛰️ Une carte photographique de la Terre toutes les 35 minutes
miniature
Pourquoi l'oxygène est-il si indispensable à autant d'êtres vivants ?
miniature
🐱 Pourquoi certains chats miaulent et ronronnent plus que d'autres ?
Page générée en 0.174 seconde(s) - site hébergé chez Contabo
Ce site fait l'objet d'une déclaration à la CNIL sous le numéro de dossier 1037632
A propos - Informations légales
Version anglaise | Version allemande | Version espagnole | Version portugaise