Fonction zêta de Riemann - Définition

Liens avec les nombres premiers

Leonhard Euler par Emanuel Handmann.

Le lien entre la fonction et les nombres premiers avait déjà été établi par Leonhard Euler avec la formule, valable pour  :

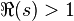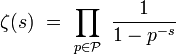
où le produit infini est étendu à l'ensemble des nombres premiers. Cette relation est une conséquence de la formule pour les suites géométriques et du théorème fondamental de l'arithmétique. On appelle parfois cette formule produit eulérien.

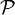
Un autre lien existe avec cette fois la fonction π(x) qui compte le nombre de nombres premiers inférieurs ou égaux à x. On a en effet

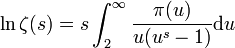
valable pour .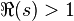

En fait, la position des zéros de la fonction de Riemann fournit la position des nombres premiers. On peut même trouver une formule exprimant chaque nombre premier en fonction des zéros de la fonction de Riemann.

Relation fonctionnelle et zéros triviaux de la fonction zêta

La fonction satisfait à l'équation fonctionnelle :

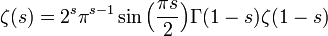
valable pour tout nombre complexe s différent de 0 et 1. Ici, Γ désigne la fonction gamma.

Une démonstration, parmi de nombreuses autres, a été donnée par Baez-Duarte en 2003. Elle est particulièrement courte. On part de la formule intégrale résultant de la formule sommatoire d'Abel (attention la borne inférieure est prise à 0, non à 1)

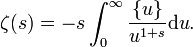
Cette égalité étant valable pour

On a ainsi, en faisant un changement de variable dans l'intégrale, posant u = 2v,

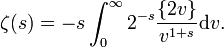
On soustrait alors les deux quantités, après avoir sorti la puissance de 2. On a ainsi

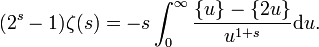
On développe la partie fractionnaire en série de Fourier

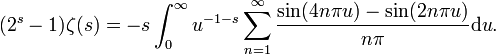
et, vérifiant les conditions habituelles pour inverser et , on obtient

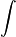
qu'on peut calculer. On trouve ainsi, en supposant cette fois , l'égalité

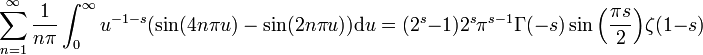
mais cette égalité reste valable pour par prolongement analytique. On obtient alors

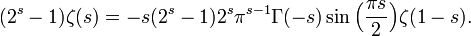
dont on déduit immédiatement la relation fonctionnelle pour On l'étend immédiatement à par le principe du prolongement analytique.

 

La fonction zêta de Riemann ζ(s) dans le plan complexe. La couleur d'un point s code la valeur de ζ(s) : des couleurs vives indiquent des valeurs proches de 0 et la nuance indique l'argument de la valeur. Le point blanc pour s = 1 est le pôle ; les points noirs sur l'axe réel négatif et sur la droite critique Re(s) = 1/2 sont les zéros.

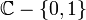
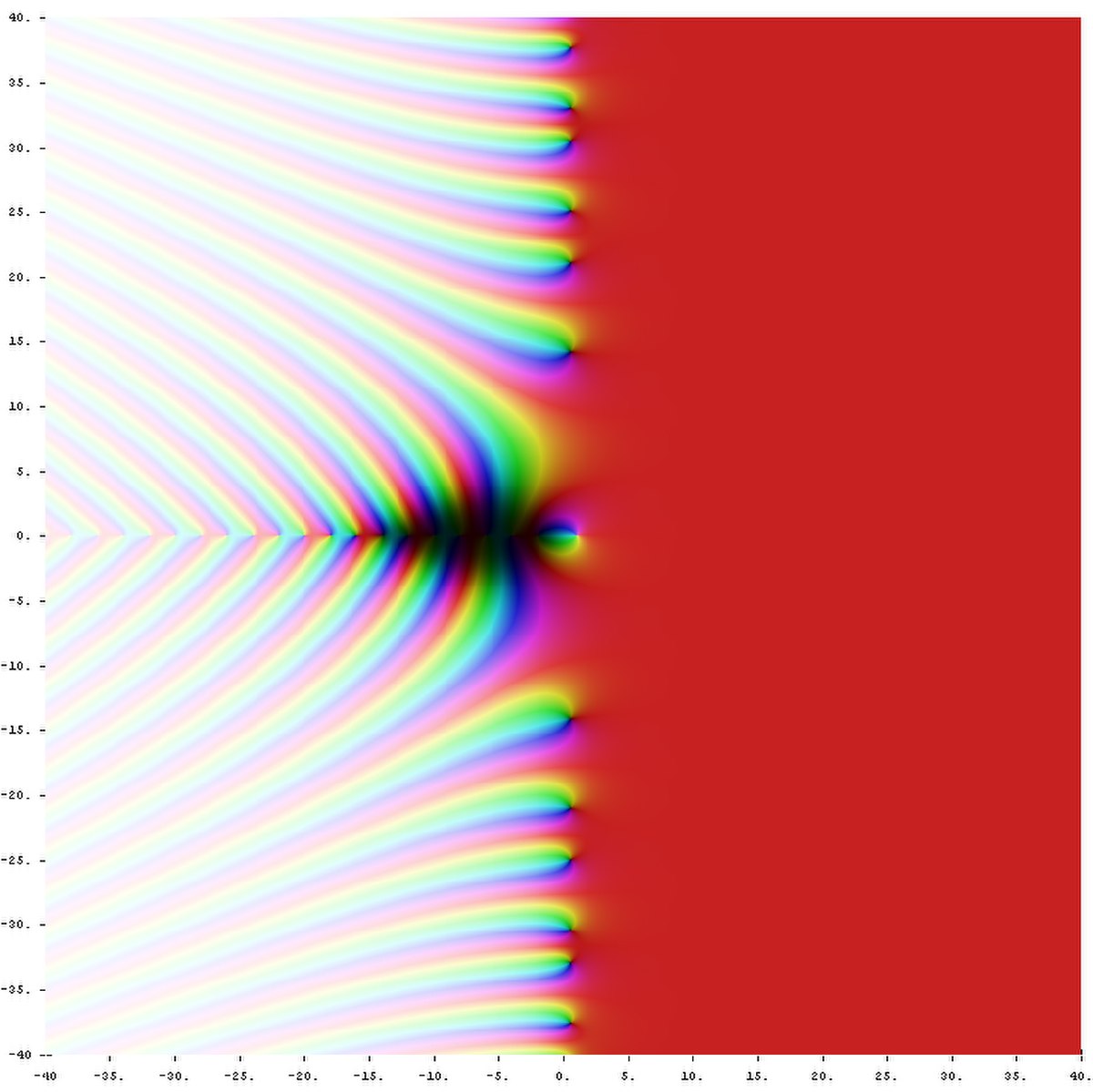
Par la relation fonctionnelle, il apparaît que la fonction s'annule pour tous les entiers de la forme , par suite du facteur mais pas en s=0 par suite du facteur ζ(1 − s). Ces zéros sont appelés zéros triviaux.

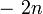
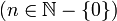
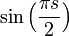
Il en existe d'autres. Une étude plus détaillée figure ci-dessous au paragraphe .

Le comportement au voisinage de 1 : théorème de Dirichlet et nombres de Stieltjes

Utilisant la formule sommatoire d'Abel, on trouve

La partie entière [u] se décompose en u − {u}. On a alors

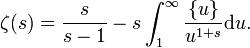
Comme {u} est toujours compris entre 0 et 1, l'intégrale est convergente et le terme est borné. Le premier terme vaut aussi

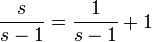
qui montre que la fonction admet un pôle d'ordre 1 en 1 et de résidu 1. Cela constitue le théorème de Dirichlet. Le développement en série de Laurent de la fonction ζ(s) s'écrit donc

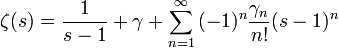
où l'on a

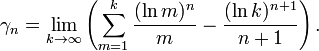
Ces nombres sont appelés nombres de Stieltjes. Concernant ces nombres, Matsuoka, en 1985, a montré que l'on avait pour n>4

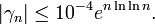
On sait aussi qu'il y a asymptotiquement la moitié de ces nombres qui sont positifs.

Thomas Joannes Stieltjes s'intéressa de près à la fonction de Riemann. Il est l'auteur d'une tentative avortée de démonstration de l'hypothèse de Riemann à partir d'une hypothèse voisine de celle de Mertens qu'il fut incapable de démontrer.

Le développement de Laurent en 1 montre que est négative sur l'axe réel avant 1 (elle est positive après 1 de manière élémentaire puisque tous les termes de la série de Dirichlet sont alors positifs). En effet, on a

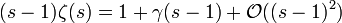
or, en supposant (s − 1) < 0 et suffisamment petit, on a

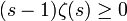
donc