Samedi 3 Mai 2025
Rechercher 🔍

Fraction continue et approximation diophantienne - Définition

Source: Wikipédia sous licence CC-BY-SA 3.0.
La liste des auteurs de cet article est disponible ici.
- Introduction - Préambule - Irrationalité - Théorème de meilleure approximation rationnelle - Autres applications

Irrationalité

Résultat de Lambert

Johann Heinrich Lambert démontre que si t est un rationnel non nul, alors tan (t) et exp(t) sont irrationnels.

Lambert est un précurseur dans son usage des approximations diophantiennes construites à l'aide de fractions continues, ce qui lui permet de montrer l'irrationalité de π. Il n'utilise pas directement la fraction continue de ce nombre, on ne dispose alors pas d'une expression comme celle d'Euler pour la base du logarithme. Si la théorie garantie l'existence d'une fraction continue égale à π, la difficulté réside dans le fait qu'il n'existe pas alors de méthode connue pour montrer que ce développement est infini.

Lambert établit tout d'abord une expression de la fonction tangente sous forme de fraction continue. Pour cela, il applique l'algorithme dit des divisions successives (cf l'article Approximant de Padé). Le problème est que ce type de démarche génère une expression appelée fraction continue généralisée, ce sont des développements d'un nombre réel x de la forme suivante, qui imposent d'autres notations :

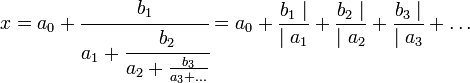
x = a_0+\cfrac{b_1}{a_1+\cfrac{b_2}{a_2+\frac{b_3}{a_3+\dots}}} = a_0 + \frac{b_1\mid}{\mid a_1} + \frac{b_2 \mid}{\mid a_2} + \frac{b_3 \mid}{\mid a_3} +\dots

Celles utilisées ici, sont dites de Pringsheim. Les résultats décrits en première partie de cet article ne s'appliquent plus. Et, à la différence des fractions continues étudiées jusqu'ici, dites simples par opposition, le fait d'autoriser des valeurs quelconques à an et bn pose le problème de la convergence, que Lambert ne d'ailleurs traite pas. Il établit un résultat dans le cas où les suites (an) et (bn) sont des entiers non nuls, qui généralise la proposition indiquant qu'une fraction continue simple infinie n'est jamais rationnelle :

  • Si les suites (an) et (bn), pour n décrivant l'ensemble des entiers positifs, forment deux suites à valeurs dans les entiers non nuls telles que |an| > |bn| + 2 pour tout n et telles que la fraction généralisée qu'elles définissent soit convergente, alors la limite est irrationnelle.

Procédons par étapes :

  • La suite des réduites des quotients complets d'indices supérieurs ou égal à 1 sont tous strictement plus petits que 1 en valeur absolue :

Ce qui signifie que si n et p sont deux entiers strictement positifs, la réduite d'indice p du quotient complet d'indice n, noté xn,p est strictement plus petite que 1 en valeur absolue :

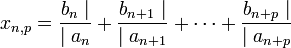
x_{n,p} = \frac{b_n\mid}{\mid a_n} + \frac{b_{n+1} \mid}{\mid a_{n+1}} + \cdots + \frac{b_{n+p} \mid}{\mid a_{n+p}}

Montrons ce résultat par récurrence sur p. Si p est égal à 1, la fraction se limite à bn / an et, comme an est strictement plus grand que bn la propriété est vérifiée.

Supposons le résultat vrai à l'ordre p et montrons le à l'ordre p + 1. la valeur xn,p+1 est égal à une fraction de numérateur bn et de dénominateur an + xn+1,p. Par hypothèse de récurrence, xn+1,p est en valeur absolue strictement plus petite que 1 et donc |an + xn+1,p| est strictement plus grand que |bn|, ce qui montre le résultat.

  • La suite des quotients complets d'indices supérieurs ou égal à 1 sont tous strictement plus petits que 1 en valeur absolue :

La proposition est presque la même que la précédente, mais on a opéré un passage à la limite sur p. Une configuration pourrait nous gêner, imaginons un quotient complet de la forme suivante :

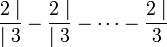
\frac{2\mid}{\mid 3} - \frac{2 \mid}{\mid 3} - \cdots - \frac{2 \mid}{3}

Un rapide calcul montre que si le premier quotient complet est égal à 1, alors la fraction continue est aussi égale à 1. Ce qui est de fait ce qui se produit. Si un quotient complet est de cette nature dans la fraction continue généralisée considérée, il est alors égal à 1, notons xp ce quotient complet. La fraction continue généralisée est égale à l'expression suivante, généralisation de la relation de récurrence :

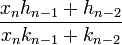
\frac {x_{n}h_{n-1} + h_{n-2}}{x_{n}k_{n-1} + k_{n-2}}

Qui est manifestement un rationnel. Pour cette raison, la distance entre |an| et |bn| a été choisie au moins égale à 2. La proposition précédente montre que les quotients complets ont une limite inférieure ou égale à 1, il suffit donc uniquement de montrer que la valeur 1 est impossible. Soit xn le quotient complet d'ordre n. Par définition il est égal à une fraction de numérateur bn et de dénominateur an + xn+1, or |an| dépasse d'au moins 2 la valeur |bn|, donc |an + xn+1| est strictement plus grand que |bn|, ce qui montre le résultat recherché.

  • La limite de la fraction continue généralisée est irrationnelle :

On raisonne maintenant par l'absurde et l'on suppose que x0 est un nombre rationnel. La relation x0 = a0 + 1/x1 montre que le quotient complet d'indice 1 est aussi rationnel. La relation x1 = a1 + b1/x2 montre que x2 est rationnel. Une récurrence montre que tous les quotients complets sont rationnels. Notons pn / qn, avec pn et qn entier, le quotient complet d'indice n. Montrons que |pn+1| est strictement inférieur à |pn|. On dispose des égalités suivantes :

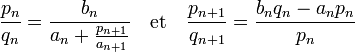
\frac {p_n}{q_n} = \frac {b_n}{a_n+ \frac {p_{n+1}}{a_{n+1}}}\quad\text{et}\quad \frac {p_{n+1}}{q_{n+1}} = \frac {b_nq_n - a_np_n}{p_n}

Il est donc possible de définir qn+1 comme égal à pn et pn+1 à bn.qn - an.pn. Rien ne garantit que les valeurs pn+1, et qn+1 soient premières entre elles, mais cela n'a guère d'importance. Comme |pn+1| est nécessairement strictement inférieur à |qn+1| car le quotient complet est, en valeur absolue, strictement inférieur à 1, |pn+1| est strictement inférieur à |pn|. Les coefficients |pn| forment une suite d'entiers positifs strictement décroissante et infinie, ce qui est absurde. Cette technique de démonstration porte le nom de méthode de descente infinie.

 

Base du logarithme népérien

Le développement en fraction continue déjà utilisée pour la fonction exponentielle n'est pas idéale, pour appliquer le résultat de Lambert. Il existe heureusement une infinité d'expressions sous forme de fraction continue d'une fonction analytique, il utilise la forme suivante, trouvée par Lagrange. La construction de cette fraction continue est disponible dans l'article Approximant de Padé de la fonction exponentielle.

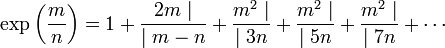
\exp \left(\frac mn\right) = 1 + \frac{2m \mid}{\mid m-n} + \frac{m^2 \mid}{\mid 3n} + \frac{m^2 \mid}{\mid 5n} + \frac{m^2 \mid}{\mid 7n} + \cdots

Il est aisé d'extraire un quotient complet satisfaisant les hypothèses de la proposition de Lambert, si m est différent de 0. Or, si un quotient complet est irrationnel, la fraction continue l'est aussi. Ce qui lui permet d'énoncer le résultat suivant :

  • L'image par la fonction exponentielle d'un nombre rationnel différent de 0 est irrationnelle.

On dispose de la fraction continue suivante, convergente sur tous les nombres complexes, et donc aussi sur les nombres rationnels :

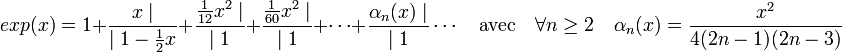
exp (x) = 1 + \frac{x\mid}{\mid 1-\frac 12x} + \frac{\frac 1{12}x^2 \mid}{\mid 1} + \frac{\frac 1{60}x^2 \mid}{\mid 1} + \cdots + \frac{\alpha_n(x) \mid}{\mid 1}\cdots\quad\text{avec}\quad \forall n\ge 2 \quad \alpha_n(x) = \frac {x^2}{4(2n-1)(2n-3)}

En multipliant le numérateur et le dénominateur de la première barre de fraction par 2 et la nième par 2(2n - 1), on obtient :

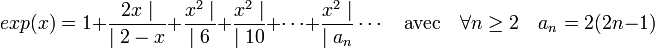
exp (x) = 1 + \frac{2x\mid}{\mid 2- x} + \frac{x^2 \mid}{\mid 6} + \frac{x^2 \mid}{\mid 10} + \cdots + \frac{x^2 \mid}{\mid a_n}\cdots\quad\text{avec}\quad \forall n\ge 2 \quad a_n = 2(2n-1)

En remplaçant x par p / q un rationnel différent de 0, et en multipliant en haut et en bas de chaque barre de fraction par q on obtient :

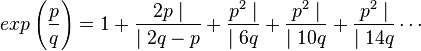
exp \left(\frac pq\right) = 1 + \frac{2p\mid}{\mid 2q- p} + \frac{p^2 \mid}{\mid 6q} + \frac{p^2 \mid}{\mid 10q} + \frac{p^2 \mid}{\mid 14q}\cdots

Il existe manifestement un indice n tel que p2 + 2 soit strictement plus petit que 2(2m - 1)q, si m est plus grand que n. Si hm / km désigne la réduite d'indice m et xn le quotient complet d'indice n, on obtient l'égalité :

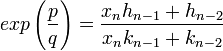
exp \left(\frac pq\right) = \frac {x_{n}h_{n-1} + h_{n-2}}{x_{n}k_{n-1} + k_{n-2}}

Or hn-1, hn-2, kn-1 et kn-2 sont des entiers non nuls et le résultat de Lambert montre que xn est un irrationnel, on en déduit bien l'irrationalité recherchée.

 

Nombre de Pythagore

Pour π, l'affaire est un peu plus délicate. Il existe bien des fractions généralisées qui approximent ce nombre, James Gregory a montré par exemple que :

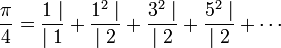
\frac {\pi}4 = \frac{1 \mid}{\mid 1} + \frac{1^2 \mid}{\mid 2} + \frac{3^2 \mid}{\mid 2} + \frac{5^2 \mid}{\mid 2} + \cdots

Cette fraction est néanmoins impropre pour l'application du résultat précédent. Lambert prend alors le problème de manière inverse, et considère une fraction continue de la fonction tangente (cette fraction continue est étudiée dans l'article Approximant de Padé).

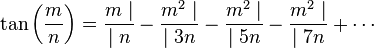
\tan \left(\frac mn\right) = \frac{m \mid}{\mid n} - \frac{m^2 \mid}{\mid 3n} - \frac{m^2 \mid}{\mid 5n} - \frac{m^2 \mid}{\mid 7n} + \cdots

Le même raisonnement que pour la fonction exponentielle s'applique et :

  • L'image par la fonction tangente d'un nombre rationnel différent de 0 est irrationnelle.

Or l'image par la fonction tangente de π/4 est égal à 1, un nombre rationnel et π/4 ne peut être rationnel.

  • Le nombre π vérifie l'égalité suivante :
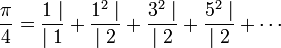
\frac {\pi}4 = \frac{1 \mid}{\mid 1} + \frac{1^2 \mid}{\mid 2} + \frac{3^2 \mid}{\mid 2} + \frac{5^2 \mid}{\mid 2} + \cdots

La fraction continue est construite de telle manière à ce que la différence entre deux réduites consécutives soit égale à (-1)n/(2n + 1), une série que James Gregory a montré comme convergente vers π/4.

Notons (hn) et (kn) les numérateurs et dénominateurs des fractions réduites, l'objectif est le calcul de δn = hn/kn - hn-1/kn-1. On dispose pour cela de l'égalité :

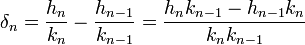
\delta_n = \frac {h_n}{k_n} - \frac {h_{n-1}}{k_{n-1}} = \frac {h_nk_{n-1} - h_{n-1}k_n}{k_{n}k_{n-1}}

Un calcul analogue à celui des fractions continues montre les relations de récurrences :

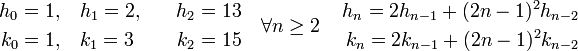
\begin{align}h_0 = 1,\quad & h_1 = 2,\quad & h_2= 13 \\k_0 = 1,\quad & k_1=3\quad & k_2= 15\end{align}\quad \forall n \ge 2 \quad \begin{align}h_n = 2h_{n-1} + (2n-1)^2h_{n-2}\\k_n = 2k_{n-1} + (2n-1)^2k_{n-2}\end{align}
L'égalité suivante est vérifiée, si n est supérieur ou égal à 1 :
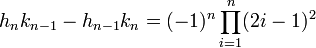
h_nk_{n-1} - h_{n-1}k_n = (-1)^n\prod_{i=1}^n (2i-1)^2

Elle correspond au calcul du numérateur de δn. Etablissons ce résultat par récurrence. Pour n égal à 1, on a :

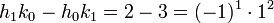
h_1k_0 - h_0k_1 = 2-3 = (-1)^1\cdot 1^2\;

Supposons le résultat vrai à l'ordre n - 1 et montrons le pour n :

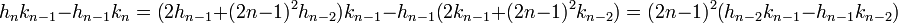
h_nk_{n-1} - h_{n-1}k_n=\big(2h_{n-1} + (2n-1)^2h_{n-2}\big)k_{n-1} - h_{n-1}\big(2k_{n-1} + (2n-1)^2k_{n-2}\big)= (2n-1)^2\big(h_{n-2}k_{n-1} - h_{n-1}k_{n-2}\big)\;

L'hypothèse de récurrence montre que :

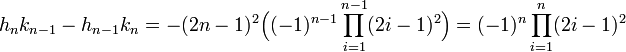
h_nk_{n-1} - h_{n-1}k_n = -(2n-1)^2\Big((-1)^{n-1}\prod_{i=1}^{n-1} (2i-1)^2\Big) = (-1)^n\prod_{i=1}^n (2i-1)^2
L'égalité suivante est vérifiée, si n est supérieur ou égal à 1 :
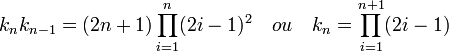
k_nk_{n-1} = (2n+1)\prod_{i=1}^n (2i-1)^2 \quad {ou}\quad k_n = \prod_{i=1}^{n+1} (2i-1)

Elle correspond au calcul du dénominateur de δn. On remarque que la formule établissant kn démontre celle donnant la valeur de kn.kn-1. Calculons encore une fois ce résultat par récurrence. Pour n égal à 1, il suffit de remarquer que k1 est égal à 3. Supposons le résultat vrai à l'ordre n - 1 et montrons le pour n :

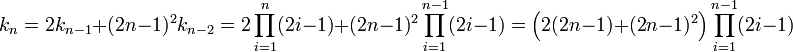
k_n = 2k_{n-1} + (2n-1)^2k_{n-2}= 2\prod_{i=1}^{n} (2i-1) + (2n-1)^2\prod_{i=1}^{n-1} (2i-1)=\Big(2(2n-1) + (2n-1)^2\Big) \prod_{i=1}^{n-1} (2i-1)

On en déduit :

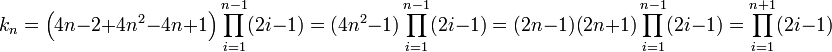
k_n =\Big( 4n - 2 + 4n^2 -4n + 1\Big)\prod_{i=1}^{n-1} (2i-1)=(4n^2 -1)\prod_{i=1}^{n-1} (2i-1)= (2n -1)(2n+1)\prod_{i=1}^{n-1} (2i-1)=\prod_{i=1}^{n+1} (2i-1)
Expression de la fraction continue généralisée comme une série :

Les deux calculs précédents offrent une expression de δn :

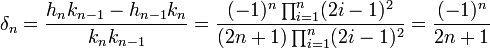
\delta_n = \frac {h_nk_{n-1} - h_{n-1}k_n}{k_{n}k_{n-1}} = \frac {(-1)^n\prod_{i=1}^n (2i-1)^2}{(2n+1)\prod_{i=1}^n (2i-1)^2}= \frac {(-1)^n}{2n+1}

On en déduit une expression de la fraction réduite :

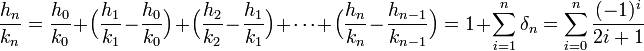
\frac {h_n}{k_n} = \frac {h_0}{k_0} + \Big(\frac {h_1}{k_1} - \frac {h_0}{k_0}\Big)+ \Big(\frac {h_2}{k_2} - \frac {h_1}{k_1}\Big)+ \cdots + \Big(\frac {h_n}{k_n} - \frac {h_{n-1}}{k_{n-1}}\Big) = 1 + \sum_{i=1}^n \delta_n = \sum_{i=0}^n \frac{(-1)^i}{2i+1}
Conclusion :

La série précédente est connue sous le nom de formule de Leibniz et converge vers π/4. La fraction continue généralisée est donc convergente et sa limite est bien celle annoncée.

 
Préambule
Théorème de meilleure approximation rationnelle
- Introduction - Préambule - Irrationalité - Théorème de meilleure approximation rationnelle - Autres applications
miniature
La face cachée de la Lune révèle une étrangeté 🌓
miniature
Piéger le CO2 sous terre indéfiniment, c'est possible ! 🌍
miniature
La plus lointaine cousine de la Voie Lactée jamais observée 🌀
miniature
Ce codex médiéval cache un secret dans son bois 🔍
miniature
Une éruption volcanique en 2018 responsable d'une explosion de vie 🌋
miniature
Un système d'exploitation pour les ordinateurs quantiques voit le jour 🖥️
miniature
Des singularités temporelles dans l'Univers ? 🕰️
miniature
Des fossiles de dinosaures mieux datés 🦖
miniature
Une gigantesque muraille de 10 milliards d'années-lumière dans l'Univers 🔭
miniature
Benchmark: les processeurs quantiques sous la loupe, quels sont les meilleurs ? 🏆
miniature
Découverte d'une "fourmi de l'enfer" vieille de 113 millions d'années 🐜
miniature
Le rôle méconnu de la décharge dans l'usure des batteries 🔋
miniature
1
La fonte des glaces déplace les pôles: quelles conséquences ? 🌍
miniature
L'appareil photo de votre smartphone peut détecter l'antimatière 📱
miniature
Cette étoile-zombie peut déformer les atomes à distance, et elle fonce dans notre galaxie ⭐
miniature
Un mosasaure géant découvert dans le Mississippi 🦕
miniature
Problème, les galaxies meurent plus tôt que prévu 🌀
miniature
Ce lien entre cannabis et troubles psychotiques 🧠
miniature
Une révolution dans le refroidissement des puces électroniques ? 🔥
miniature
Des parasites sous-marins filmés en train de vampiriser un poisson des abysses 👀
miniature
Lucy survole un astéroïde en forme de cacahuète 🚀
miniature
Découverte du fossile d'un dinosaure géant méconnu 🦕
miniature
Mars avait-elle un champ magnétique unilatéral ? 🔍
miniature
Des chimpanzés surpris à sociabiliser avec de l'alcool 🍇
miniature
Découverte macabre: ce gladiateur a été tué par un lion il y a 1 800 ans... en Grande-Bretagne 🦁
miniature
L'électroluminescence du graphène, une découverte inattendue ! 💡
miniature
Cet objet métallique n'a pas été fabriqué sur Terre 🔧
miniature
1
Cette innovation permet aux voitures électriques de charger 6 fois plus vite par grand froid ⚡
miniature
Cette super-Terre brûle les attentes des astronomes 🔥
miniature
Découverte exceptionnelle de fossiles d'amphibiens géants 🐸
miniature
Voici ce qui a causé les toutes premières inégalités de richesse 💰
miniature
Quelle est cette zone étrange dans l'Atlantique Nord ? 🌊
miniature
Cette planète orbite à angle droit autour de deux étoiles, une première ! 🔭
miniature
Des cellules solaires flexibles battent des records d'efficacité ⚡
miniature
Ce dispositif reproduit les trous noirs et trous blancs en laboratoire 🌀
miniature
Record établi pour un transistor en diamant 💎
miniature
Les sursauts radio rapides trahissent enfin leur origine cosmique 📡
miniature
Ces biomarqueurs sanguins prédisent la démence 10 ans à l'avance 🧠
miniature
Découverte majeure: des médicaments 23 fois plus efficaces contre le cancer 💊
miniature
Les oscillations collectives des foules humaines denses 🔁
miniature
Une forme inconnue de la matière détectée au LHC ? ⚛️
miniature
Le sel, un facteur méconnu de l'obésité ? 🧂
miniature
L'Univers en rotation, une réponse élégante à ce problème astrophysique majeur 🌀
miniature
Découverte tectonique majeure sous les Petites Antilles 🌍
miniature
1
Peut-on geler en chauffant ? ❄️
miniature
Une peau électronique pour doter les robots du sens du toucher 👌
miniature
Invention d'un bois semi-transparent avec une technique...surprenante ! 🌳
miniature
Le cancer inscrit dans nos gènes dès la naissance ? 🧬
miniature
Des supernovae à l'origine de deux extinctions massives sur Terre ? 💥
miniature
Le passé verdoyant du plus grand désert du monde 🐪
Page générée en 0.135 seconde(s) - site hébergé chez Contabo
Ce site fait l'objet d'une déclaration à la CNIL sous le numéro de dossier 1037632
A propos - Informations légales
Version anglaise | Version allemande | Version espagnole | Version portugaise