Fraction continue et approximation diophantienne - Définition
La liste des auteurs de cet article est disponible ici.
Introduction
En mathématiques, la réduite d'une fraction continue d'indice n, c'est-à-dire la fraction limitée à n étapes, est une approximation diophantienne de la valeur initiale. Plus précisément, la suite des réduites de rangs pairs approxime par défaut le réel et celle des rangs impairs par excès. Réciproquement, si l'on considère une suite (an) telle que a0 est un entier et an un entier strictement positif si n est supérieur à zéro, la suite des réduites de la fraction continue admettant les an comme coefficients converge vers une limite finie x (qui est un réel irrationnel si, et seulement si, la suite est infinie) dont le développement en fraction continue (qui est unique dans ce cas où x n'est pas rationnel) est la fraction continue de coefficients an.
Les fractions réduites hn / kn fournissent en un certain sens les meilleures approximations rationnelles d'un nombre réel : la réduite d'indice n est une approximation située à une distance de x inférieure à 1 / kn2, et, si une fraction p / q est une approximation située à une distance de x inférieure à 1 / 2.q2 alors p / q est une réduite de x. Ce résultat porte le nom de théorème de meilleure approximation.
Ces résultats ne sont pas sans conséquence. Les fractions continues sont utilisées pour approcher des nombres irrationnels comme des racines carrées ou π. Cette propriété permet de résoudre certaines équations diophantiennes comme celle de Pell-Fermat. Elle offre de plus une condition nécessaire et suffisante pour qu'un nombre soit rationnel, à l'origine de la première démonstration de l'irrationalité de e, la base du logarithme népérien. Elle permet d'aller plus loin et ce sont les propriétés des approximations diophantiennes obtenues à l'aide de fractions continues qui permettent de construire les premiers nombres démontrés transcendants, puis de montrer que e et π sont transcendants.
Préambule
Généralités
Les exemples les plus simples se trouvent dans l'article Fraction continue, et concernent les rationnels. Un nombre rationnel x se représente de la manière suivante :
![x = a_0 + \cfrac 1{a_1 + \cfrac 1{a_2 + \frac 1{a_3 + \frac 1{\cdots + \frac 1{a_n}}}}} = [a_0, a_1,a_2 ,a_3, \cdots , a_n]](https://static.techno-science.net/illustration/Definitions/autres/7/7c3bebef20f91e85a4b23f3074dc3217_97cc9b7ba9176e0f1cbf77ff816c0fc9.png)
Les deux notations, avec des barres de fractions ou des crochets signifient la même chose. Si p est un entier inférieur à n, le terme ap, appelé coefficient d'indice p, désigne un entier strictement positif sauf peut être a0 qui est un entier quelconque. La fraction qui s'arrête au terme ap est la réduite d'indice p et si 1/ xp+1 est le complément à ajouter dans l'expression à ap pour obtenir la valeur exacte de x, alors xp+1 est appelé quotient complet d'indice p + 1, ce qui se traduit par l'égalité :
![x = [a_0, a_1, a_2, \cdots , a_p, x_{p+1}]](https://static.techno-science.net/illustration/Definitions/autres/1/18f42fd19cbaac970946aa80a40ccc9c_d07f5dac6eadefa21c2a0e8abd9f637e.png)
Ce concept ne se limite pas aux rationnels. Si x est un nombre irrationnel, la suite des coefficients est infinie et celle des réduites est alternée et converge vers x. Pour toute suite d'entiers an strictement positifs, à l'exception éventuelle de a0 qui peut être négatif ou nul, la suite des réduites construites à l'aide des coefficients an converge vers un nombre réel r dont la fraction continue est constituée des coefficients an. Un exemple simple de cette nature est proposé dans l'article fraction continue d'un nombre quadratique. Un nombre quadratique est une solution d'une équation du second degré à coefficients rationnels. La fraction continue d'un nombre x est périodique à partir d'un certain rang, si, et seulement si, x est quadratique.
Quelques résultats sont bien utiles, ils sont démontrés dans l'article détaillé. Si hn / kn désigne la réduite d'ordre n, on dispose des relations de récurrence suivantes :
![h_{n+1} = a_{n+2}h_{n+1} + h_n,\quad k_{n+1} = a_{n+2}k_{n+1} + k_n\quad\text{et}\quad \left[a_0, a_1, \,\dots, a_{n-1}, x_n \right]= \frac{x_n h_{n-1}+h_{n-2}} {x_n k_{n-1}+k_{n-2}}](https://static.techno-science.net/illustration/Definitions/autres/d/d64230417b387b157adf7e70a4002668_e762c719d588b6c6076de88046288c66.png)
Ce qui montre que les numérateurs et les dénominateurs des réduites forment deux suites qui tendent vers l'infini. On dispose encore résultats suivants :
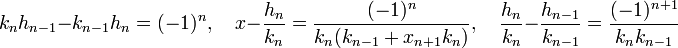
Exemple, la base du logarithme népérien

Leonhard Euler cherche l'expression en fraction continue du nombre e, base du logarithme népérien. Pour cela, il commence par établir l'expression de la fonction exponentielle, sous forme de fraction continue :
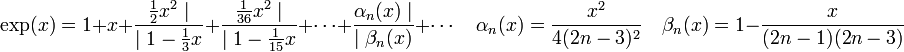
Une expression de cette nature est appelée approximant de Padé. La précédente permet d'exprimer e sous forme de fraction continue :
![\text{e} = [2,\overbrace{1,2,1},\overbrace{1,4,1},\cdots , \overbrace{1,2p,1},\cdots \,] = [2,\overline{1, 2p,1}]\quad p \in \mathbb N - \{0\}](https://static.techno-science.net/illustration/Definitions/autres/8/8beb71025713cfbf5cee442946938c18_b5a82233b8013636635707910273c2b2.png)
La barre utilisée ici est une notation fréquente. Elle signifie une répétition à l'infini de la suite des entiers couverte par la barre. Le premier intérêt que le peut y trouver est le fait d'obtenir une valeur approchée de e. La réduite d'ordre 2 est égal à 2,75 et celle d'ordre 10 propose 7 chiffres significatifs. Cependant, une approche par la série entière propose un résultat analogue avec moins d'effort. Euler remarque que l'expression en fraction continue de e est infinie, ce qui est une condition nécessaire est suffisante pour montrer que e n'est pas un rationnel, l'objectif de sa démonstration. On peut néanmoins encore trouver des démonstrations plus simples de ce résultat, un exemple est proposé dans l'article e (nombre). Ce résultat permet d'aller un peu plus loin, puisqu'il prouve que e n'est solution d'aucune équation du second degré à coefficients rationnels, car son développement en fraction continue n'est pas périodique. Ce type de démarche ne permet pas d'aller au-delà. De nouvelles idées sont nécessaires, par exemple, pour montrer la transcendance de e.
Malgré ces limitations, les fractions continues qui offrent des suites rationnelles convergeant vers e sont riches en informations sur la nature arithmétique de la limite. La suite de l'article montre, par exemple que si t est rationnel, alors et ne l'est pas. La démarche, à l'origine de la preuve, permet aussi d'établir l'irrationalité de π .
-
- Démarche :
L'approche utilisée ici consiste à étudier la valeur du nombre ayant pour fraction continue les coefficients 2, 1,2,1, 1,4,1, ... . L'article Fraction continue montre que la suite des fractions réduites (hn / kn) est convergente, que sa limite x admet pour développement en fraction continue celle des coefficients utilisés et qu'il n'existe qu'un unique nombre réel ayant pour fraction continue exactement la suite des coefficients utilisés.
Pour trouver la limite de la suite des fractions réduites, il suffit de trouver celle de n'importe quelle suite extraite. L'aspect quasi-périodique de la fraction continue amène à considérer la suite (h3p / k3p).
-
- Matrice :
Dans toute fraction continue, hn et kn vérifient une relation de récurrence linéaire, généralisant celle de la suite de Fibonacci. Cette relation s'exprime sous forme de matrice 2x2 :
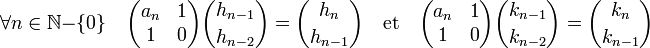
La quasi périodicité de la fraction continue étudiée ici justifie les définitions suivantes :
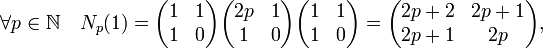
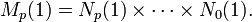
On trouve les premières valeurs suivantes, pour la suite Mp(1) :
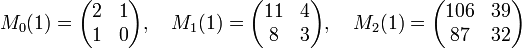
Une simple récurrence montre que la première ligne de la matrice Mp(1) correspond aux coefficients (h3p, k3p) et la deuxième ligne à (h3p-1, k3p-1). La démonstration se limite ainsi à montrer que la fraction formée par les termes de la première ligne de la matrice possède pour limite la base du logarithme.
-
- Approximant de Padé
La fonction exponentielle possède des propriétés analytiques fortes. Ces propriétés sont essentielles pour mener à bien la démonstration, cette approche est à la base de la notion d'approximant de Padé. Une méthode consiste à considérer les matrices Mp(t) comme une généralisation de la définition précédente. Elles représentent des fonctions de l'ensemble des nombres réels dans l'espace des matrices 2x2 à coefficients réels. Chaque coefficient de la matrice est un polynôme. La définition précise est la suivante :
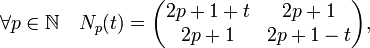
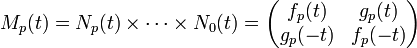
Si t est égal à 1, on retrouve les expressions matricielles précédentes, en ce sens, se sont bien des généralisations. La définition de la matrice Np(t) donne les expressions par récurrence :
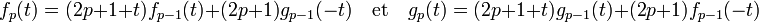
On remarque en effet que si fp(t) et gp(t) désigne les coefficients de la première ligne de la matrice Mp(t), les coefficients de la deuxième ligne sont gp(-t) et fp(-t). On obtient, pour premières expression des suites (fp(t)) et (gp(t)) :
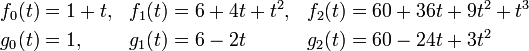
Il suffit alors de démontrer que la fraction fp(t) / gp(t) converge vers la fonction exponentielle. Cette preuve se trouve dans l'article Approximant de Padé.
Fragments d'histoire
L'idée d'approximer un nombre à l'aide d'une fraction continue remonte à l'origine du concept, aux Indes du Ve siècle. Avec la résolution de l'identité de Bézout, c'est la première motivation qui pousse à l'usage d'une telle notion. Âryabhata l'utilise pour les deux usages et particulièrement pour extraire des racines carrées.
La propriété d'approximation des fractions continues est retrouvée accidentellement sur la racine de 13 par Rafael Bombelli puis généralisée par Pietro Antonio Cataldi à toutes les racines carrées. William Brouncker utilise cette méthode pour obtenir une approximation de π exacte à 10 décimales. Leonhard Euler développe l'aspect théorique de la méthode. Il montre que tout nombre réel admet un unique développement en fraction continue simple et qu'il est irrationnel si, et seulement si cette fraction continue est de longueur infinie. Il invente une méthode, maintenant connue sous le nom d'approximant de Padé pour déterminer celui de e, la base du logarithme népérien, ce qui est la première démonstration de son irrationalité. Johann Heinrich Lambert pousse plus loin l'exploration et montre que π n'est pas non plus rationnel.
L'usage d'une fraction continue comme approximation diophantienne pour étudier la nature arithmétique d'un nombre est établi. Le XIXe siècle est celui d'une meilleure compréhension des nombres transcendants. Joseph Liouville en utilise une pour exhiber le premier nombre démontré transcendant. Si le savoir décrit dans cet article s'arrête là, l'histoire, elle, continue. Parmi les multiples progrès, on peut citer Charles Hermite qui établit la transcendance de e en 1873. Puis, à l'aide d'une méthode analogue, Ferdinand von Lindemann montre celle de π.


















































