Fraction continue et approximation diophantienne - Définition

Théorème de meilleure approximation rationnelle

A certains égards, les réduites forment les meilleures approximations diophantiennes, et réciproquement une bonne approximation rationnelle est nécessairement une réduite de la fraction continue :

• Pour tout entier n la majoration (1) est vérifiée. Sur deux réduites consécutives, il en existe une qui vérifie la majoration (2) :

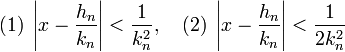
C'est en ce sens que l'approximation diophantienne est bonne. Une approximation décimale possède une précision de l'ordre de 1 / 2.q et dans le cas général, il n'est guère possible de faire mieux avec les représentations décimales. Une réduite approche la valeur x non pas en fonction de l'inverse du dénominateur, mais de son carré. Si l'on parle aussi de meilleure approximation, c'est parce-qu'il existe une réciproque au résultat précédent, appelée théorème de meilleure approximation rationnelle. Ici, n désigne un entier strictement positif.

• Soient h et k deux entiers tels que 0 < k < k_n+1. La majoration suivante est vérifiée. De plus l'égalité n'a lieu que si k (resp. h) est égal à k_n (resp. h_n) :

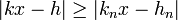
Dire que h / k approche bien x, revient à dire que k.x - h est petit. Le théorème indique que h / k n'approche jamais mieux x que la réduite d'indice n, si k est strictement plus petit que le numérateur de la réduite d'ordre n + 1 et si h / k approche aussi bien x que la réduite d'indice n, c'est qu'il y a égalité. Le terme mieux approcher est pris ici dans un sens particulier, on dit ici que la fraction 1/1 approche mieux 1,15 que, par exemple 11/10 car |1x1,15 - 1| est plus petit que 1/5, alors que |10x1,15 - 11| est plus grand. Pourtant 1/1 est plus loin de 1,15 que 11/10. La qualité de l'approximation est fonction de la valeur du dénominateur.

Ce théorème possède le corolaire suivant, permettant de déduire assurément qu'une fraction est une réduite. Il est utilisé pour l'étude des fractions continues périodiques (cf Fraction continue d'un nombre quadratique).

• Si h et k sont deux entiers qui vérifient la majoration suivante, la fraction h / k est une réduite de x.

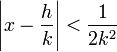
Ces différents résultats permettent de caractériser un nombre irrationnel. On sait en effet que seuls les irrationnels possèdent une infinité de réduites, et donc une infinité d'approximations diophantiennes dont la précision dépasse l'inverse du double du carré du dénominateur :

• Un nombre x réel est irrationnel, si et seulement si, pour tout entier positif N il existe une fraction p / q approximant x avec une précision meilleure que 1 / 2q² et tel que q soit supérieur à N.

Ainsi, un irrationnel se caractérise par le fait qu'il s'approche mieux qu'un rationnel par une approximation diophantienne. D'autres théorèmes sont de même nature. Celui de Liouville est une forme de réciproque généralisée du résultat précédent, indiquant que plus le degré du polynôme minimal d'un nombre algébrique est faible, moins bonne sera l'approximation diophantienne. Plus un nombre algébrique est irrationnel dans le sens où son polynôme minimal est élevé, plus on peut espérer l'approcher précisément par un rationnel. Les meilleurs candidats étant certains nombres transcendants.

Le théorème d'Hurwitz indique une limite basse de la qualité des approximations diophantiennes de tous les irrationnels. Il indique que si x est un nombre irrationnel, il existe une infinité de fraction a / b où a et b sont des nombres entiers premiers entre eux tel que :

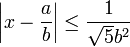
La valeur √5 est la plus élevée satisfaisant la majoration précédente. Au-delà le nombre d'or n'admet plus une infinité d'approximations satisfaisant le critère. En ce sens, le nombre d'or est l'irrationnel qui s'approxime le plus mal par des fractions. Etrangement, cet argument est utilisé pour parler du nombre d'or comme le plus irrationnel de tous les irrationnels.

Dans toute la suite des démonstrations, a_n désigne le coefficient d'indice n de x, un nombre réel, x_n son quotient complet d'indice n et h_n / k _n sa réduite d'indice n. Les propositions démontrées dans le paragraphe propriétés sont utilisées ici.

• Pour tout entier n :

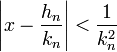
On part de l'égalité suivante :

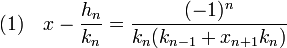
On remarque que x_n+1 est plus grand que a_n+1, donc l'expression x_n+1.k_n + k_n-1 est supérieure à a_n+1.k_n + k_n-1, égal à k_n+1, d'après les formules de récurrences donnant l'expression de la réduite. Ce qui permet de déduire que :

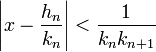
Il suffit de remarquer que k_n+1 est plus grand que k_n pour conclure.

• Sur deux réduites consécutives, il en existe une qui vérifie :

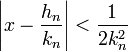
La valeur x se situe entre deux réduites consécutives quelconque et qui forment un intervalle de longueur :

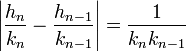
La valeur x se situe entre h_n / k_n et h_n+1 / k_n+1. Ce qui signifie que x - h_n / k_n et h_n+1 / k_n+1 - x sont de même signe, et en conséquence :

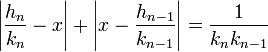
De plus, si a et b sont deux réels strictement positifs distincts 2.a.b est strictement inférieur à a² + b². On en déduit :

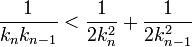
Ce qui démontre la majoration suivante :

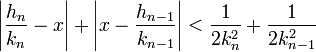
Et termine la démonstration.

• Soit n un entier strictement positif et h et k deux entiers et tel que 0 < k < k_n+1. La majoration suivante est vérifiée, de plus l'égalité n'a lieu que si k (resp. h) est égal à k_n (resp. h_n) :

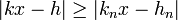
La matrice M suivante a un déterminant égal à 1 en valeur absolue, c'est-à-dire un entier inversible. Elle définit donc un endomorphisme inversible de Z² (ici Z désigne l'anneau des nombres entiers). En conséquence, il existe un vecteur colonne U tel que :

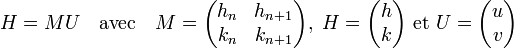
On remarque de U est à coefficients entiers car H et M ^-1 sont à coefficients entiers.

Les entiers u et v sont non nuls :

Si u est nul alors k=v.k_n+1, avec v entier, ce qui est en contradiction avec les inégalités 0 < k < k_n+1.

Si v est nul alors h / k est égal à h_n / k_n et la proposition est démontrée.

Les valeurs u et v sont de signes contraires :

Si v est négatif il est alors strictement négatif. L'égalité k = k_n.u + k_n+1.v et le fait que k soit strictement positif montrent que u est positif.

Si v est positif il est alors strictement positif. L'égalité k = k_n.u + k_n+1.v et le fait que k soit strictement inférieur à k_n+1 montrent que u est négatif.

Conclusion :

Le calcul suivant :

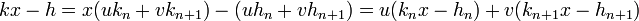
et le fait que u et v soient de signes contraires tout comme x.k_n - h_n et x.k_n+1 - h_n+1 montrent que :

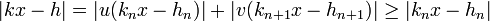
En effet, u et v sont non ous les deux nuls et x.k_n - h_n ne l'est pas non plus. L'égalité ne peut avoir lieu que si u est égal à 1 et v à 0, ce qui suppose l'égalité entre h/k et la réduite d'indice n.

• Si la majoration suivante est vérifiée, h / k est une réduite de x :

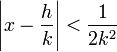
Par construction de la suite, il existe un entier n tel que :

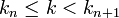
L'inégalité triangulaire et la proposition précédente montrent que :

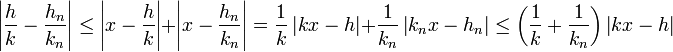
En multipliant la majoration précédente par k.k_n, on obtient :

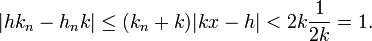
Or l'expression |h.k_n - k.h_n| prend sa valeur dans les entiers positifs, le seul entier positif strictement plus petit que 1 est 0, on en déduit qu'elle est nulle, ce qui termine la démonstration.