Fraction continue et approximation diophantienne - Définition

Autres applications

Equation de Pell-Fermat

L'équation de Pell-Fermat est l'équation suivante, où d désigne un entier positif non carré parfait.

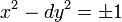
A tout couple de solution (a, b) de cette équation, correspond la fraction a / b, qui se trouve être une approximation de la racine de d. Cette approximation est à une distance inférieure à 1/2.b² de la racine, c'est donc une réduite de la fraction continue. Cette propriété peut être utilisée pour élucider la structure de l'ensemble des solutions. Elle offre aussi un algorithme d'extraction de racine carrée dont le nombre de décimales exactes double à chaque étape.

Automate de Huygens

Une application curieuse provient de l'horlogerie. Christian Huygens souhaite réaliser un automate planétaire, c'est-à-dire un système à manivelle représentant le mouvement des différentes planètes du système solaire. Sachant que le rapport entre une année terrestre et celle de Saturne est approximativement égal à 2 640 858/77 708 431, comment choisir le nombre de dents pour les différents engrenages qui composent la machine ? L'approximation diophantienne que représente la fraction continue lui offre une solution : « Or, lorsqu’on néglige à partir d’une fraction quelconque les derniers termes de la série et celles qui la suivent, et qu’on réduit les autres plus le nombre entier à un commun dénominateur, le rapport de ce dernier au numérateur sera voisin de celui du plus petit nombre donné au plus grand; et la différence sera si faible qu’il serait impossible d’obtenir un meilleur accord avec des nombres plus petits. »

Transcendance

Joseph Liouville utilise des approximations diophantiennes pour construire explicitement un nombre transcendant.

Le fait qu'il n'existe qu'un nombre fini de fractions p / q à une distance inférieure à 1/2.q² du rationnel signifie qu'un nombre rationnel s'approche « mal » par des fractions. Cette idée se généralise aux solutions d'une équation polynomiale de degré n. Soit α un nombre réel solution de l'équation f(x) = 0, où f désigne un polynôme de degré n à coefficients rationnels. Le théorème de Liouville donne une limite à la qualité de l'approximation de α par un nombre rationnel p / q ; précisément, il indique qu'il existe une constante réelle A telle que pour tout rationnel p/q :

Ce qui permet de construire une fraction continue de limite x qui n'est solution d'aucune équation polynomiale à coefficients rationnels, c'est-à-dire un nombre transcendant. Liouville l'exprime ainsi : « Il suffira de donner aux quotients incomplets [note : appelés réduites dans cet article] un mode de formation qui les fasse grandir au-delà du terme indiqué, pour obtenir une fraction continue dont la valeur ne pourra satisfaire aucune équation algébrique ... »

Une méthode consiste à construire une suite (a_n) d'entiers strictement positifs et de considérer x le nombre réel ayant la suite (a_n) comme fraction continue. La suite (a_n) est définie en posant l'entier a₀ égal à 1, et par la formule de récurrence :

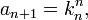
où (h_n) et (k_n) désignent encore les suites des numérateurs et dénominateurs (à valeurs positives) des réduites d'indice n du développement de x. Les résultats d'approximation d'un nombre réel par les convergeants de son développement en fraction continue donne alors la majoration :

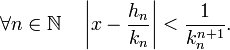
Ceci permet de montrer que le nombre x ainsi construit est transcendant grâce au théorème de Liouville.