Géométrie de l'espace-temps dans les repères tournants - Définition

Absence de courbure spatio-temporelle dans le référentiel tournant

La passage d'un système de coordonnées inertiel à un référentiel tournant est un simple changement de coordonnées spatio-temporelles. Il ne peut donc pas modifier la courbure spatio-temporelle. Elle doit donc rester nulle. Les calculs de cette section servent uniquement à vérifier ce résultat (que l'on connaît déjà). Ils n'ont donc pas grand intérêt. On pourra les sauter sans grand dommage et passer à la section suivante nettement plus intéressante.

Nous allons travailler en coordonnées polaires . Comme on se place en Relativité Restreinte, l'espace-temps est plat. Dans le référentiel inertiel R, la métrique de Minkowski s'écrit en coordonnées polaires : ds² = − c²dt² + dρ² + ρ²dφ²

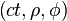
C’est-à-dire que nous avons la métrique

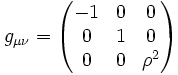
Si on utilise un référentiel R' tournant attaché au disque, nous avons immédiatement

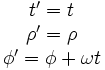
Ce qui nous donne

dφ'² = dφ² + 2ωdφdt + ωdt²

En prenant en compte ce résultat dans l'expression de l'intervalle, nous trouvons

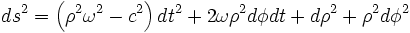
Soit le tenseur métrique

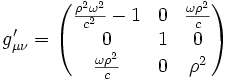
Pour un point au repos sur le disque en rotation, on trouve avec l'intervalle

, soit le ralentissement habituel du temps de l'observateur tournant.

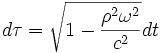
En utilisant et le tenseur métrique ci-dessus, on trouve

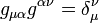
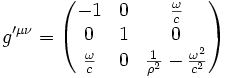
La formule pour les symboles de Christoffel est

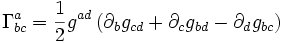
Avec les expressions du tenseur métrique on trouve les seuls symboles non nuls

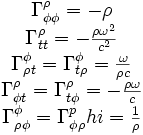
Le tenseur de courbure de Riemann - Christoffel vaut

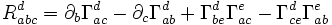
Cela donne bien . La métrique spatio-temporelle du référentiel tournant est donc bien plate. C'est normal puisque nous sommes dans un espace-temps de Minkowski. Changer de système de coordonnées ne change pas l'espace-temps.

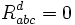
Par contre, nous allons voir dans la section suivante que la métrique spatiale, caractérisant les distances mesurées par les observateurs tournants avec leurs mètres affectés par la contraction de Lorentz, n'est pas plate. Il ne faut pas confondre métrique spatio-temporelle et métrique spatiale.

Calcul de la circonférence

Attaquons maintenant le calcul de la circonférence du disque d'une manière un peu plus précise que celle postulée dans l'étude de l'effet Sagnac.

Calcul relativiste de la circonférence d'un disque tournant

Soit un disque de rayon R et de vitesse angulaire ω tournant dans un référentiel inertiel R. Soit R' le référentiel des observateurs au repos sur le disque tournant. Un observateur au repos dans R' situé en périphérie du disque se déplace à la vitesse V = ωR. En mettant leurs petits mètres bout à bout, les observateurs au repos dans le référentiel inertiel R et situés le long de la périphérie du disque mesurent une circonférence du disque égale (bien sûr) à C = 2πR.

Au contraire, les observateurs situés dans le référentiel tournant R' ont des petits mètres contractés par la contraction de Lorentz (lorsqu'ils sont orientés dans la direction circonférentielle). Le long de la périphérie du disque, ces mètres tournants ont donc une longueur valant (quand cette longueur est mesurée dans le référentiel inertiel R). Bien sûr, les observateurs tournants n'en savent rien car la contraction de Lorentz est localement inobservable. Par contre, en mettant ces petits mètres bout à bout, les observateurs tournants situés le long de la périphérie du disque auront la surprise de trouver une circonférence du disque plus grande que 2πR valant .

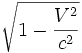
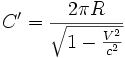
C'est le pendant, en termes de contraction de Lorentz des distances, du paradoxe de Langevin (vieillissement moins important du jumeau tournant R' en raison du ralentissement des horloges tournantes dû à la dilatation temporelle des secondes de ces horloges, y compris bien sûr les horloges biologiques qui n'ont rien de spécifique). Cela souligne le caractère local (et non global, distinction pas toujours comprise) des symétries relativistes.

La métrique spatio-temporelle du référentiel tournant reste bien sûr la métrique de Minkowski car, en Relativité Générale, un changement de système de coordonnées n'affecte pas la métrique spatio-temporelle (l'espace-temps reste plat au passage de R à R'). Par contre, la géométrie spatiale dans R' (la mesure des distances) n'est pas Euclidienne. La circonférence du disque mesurée par les observateurs tournants est plus grande que 2πR. On dit du disque tournant qu'il a (pour les observateurs tournants) une courbure spatiale négative.

Géométrie et calculs

Bien que l'on soit en Relativité Restreinte, on peut très bien utiliser la notion de métrique et le calcul tensoriel tels qu'ils sont utilisés en relativité générale. C'est d’ailleurs déjà ce que l'on fait lorsque l'on travaille en coordonnées polaires. En effet, en coordonnées polaires, le tenseur métrique de Minkowski n’a pas sa représentation canonique (rappelée ci-dessous).

Dans un système de coordonnées inertiel, la métrique de Minkowski (l'intervalle) s’écrit : , soit encore ds² = η_μνdx^μdx^ν avec η₀₀ = 1 η₁₁ = − 1 η₂₂ = − 1 η₃₃ = − 1 les coefficients extra-diagonaux de η_μν étant nuls. Plus généralement, dans un repère quelconque (un système de coordonnées non nécessairement orthonormé) cette même métrique s’écrit :

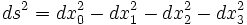
ds² = g_μνdx^μdx^ν où g_μν est l’expression du tenseur métrique dans le système de coordonnées choisi.

Dans un espace-temps de Riemann quelconque, la valeur du tenseur métrique peut varier de point en point de manière tout à fait quelconque. En général, il n'est alors pas possible de trouver un changement de repère (c’est-à-dire un changement de système de coordonnées) qui permette de ramener la métrique à la forme de Minkowski. C’est possible seulement si l’espace-temps est plat. Par contre, il est toujours possible de se ramener à la métrique de Minkowski, en un point donné de l'espace-temps, par un changement de système de coordonnées approprié.

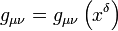
Nous supposerons connus les quelques outils propres aux géométries Riemanniennes (symboles de connexion de Christoffel, tenseur de courbure de Riemann…). Cela dit, on peut comprendre le détail des calculs effectués (comme le calcul du tenseur de courbure par exemple) sans un bagage mathématique élaboré à condition de consulter préalablement les références nécessaires .

Par contre, une connaissance élémentaire (niveau certificat de fin d’étude) de ce qu’est la longueur d’une courbe est indispensable pour parvenir à comprendre ce que représente une métrique spatiale. La longueur d’une courbe, c'est le nombre de mètres (de centimètres, de millimètres...) que l'on doit mettre bout à bout pour aller de l'origine à l'extrémité de cette courbe en la suivant. Si cette connaissance géométrique de base n’est pas bien assimilée, on ne peut pas espérer comprendre ce que représente une métrique spatiale.