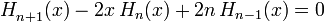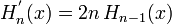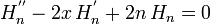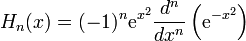Hermitien - Définition
Source: Wikipédia sous licence CC-BY-SA 3.0.
La liste des auteurs de cet article est disponible ici.
La liste des auteurs de cet article est disponible ici.
Polynômes orthogonaux d'Hermite
Les polynômes d'Hermite interviennent dans la théorie de l'approximation uniforme des fonctions. En physique, on les retrouve dans la résolution de l'équation de la chaleur, mais aussi en mécanique quantique où ils donnent les fonctions d'ondes de l'oscillateur harmonique.
La suite des polynômes d'Hermite, notés Hn, est orthogonale pour le produit scalaire défini par :
 .
.
Ces polynômes sont définis de telle manière que Hn soit de degré n, le premier d'entre eux étant H0 = 1.
Cette suite satisfait les relations suivantes :