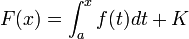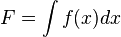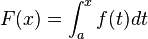Intégrale indéfinie - Définition

Introduction

En analyse réelle ou complexe, une intégrale indéfinie d'une fonction f intégrable sur un intervalle I est une fonction définie sur I par

où a est un élément de I et K une constante

Lorsque f est une fonction continue, F est une primitive de f , c'est-à-dire que la dérivée de F donne f (F' = f). On prend alors l'habitude de noter toute primitive de f sous forme

et de confondre intégrale indéfinie et primitive

Lorsque f n'est pas continue, il n'y a pas de correspondance simple entre intégrale indéfinie et primitive.

Cas de la fonction continue

Toute fonction continue sur un intervalle I est intégrable sur tout intervalle fermé inclus dans I. Le théorème fondamental de l'analyse affirme que pour tout réel a de I, la fonction définie sur I par

est la primitive de f qui s'annule en a.

Les primitives de f sont donc les intégrales indéfinies

La constante K est nécessaire pour couvrir l'ensemble des primitives possibles de f.

Cas de la fonction non continue

Durant 4 siècles, les mathématiciens, de Torricelli à Jaroslav Kurzweil et Ralph Henstock en passant par Leibniz, Euler, Cauchy, Riemann, Lebesgue, Denjoy et Perron, se sont efforcés de rechercher un lien fort entre intégrale d'une part et primitive d'autre part. Tant que le travail s'effectue sur les fonctions continues, la relation est simple, et c'est Cauchy qui en fournit la preuve (26ème leçon du Résumé des leçon données à l'école royale polytechnique sur le calcul infinitésimal en 1823). Ce résultat établi, les recherches se portent sur le cas des fonctions non continues. Riemann, puis Lebesgue, puis Kurzweil et Henstock s'efforcent de présenter des définitions de l'intégrabilité qui permettent d'élargir la relation entre intégrale indéfinie et primitive.

Intégrale indéfinie d'une fonction Riemann-intégrable

L'intégrale indéfinie d'une fonction Riemann intégrable est toujours continue. Elle est de plus dérivable en tout point où la fonction initiale est continue. Ce résultat est démontré par Darboux et du Bois Reymond en 1875. Mais la relation entre intégrale indéfinie et primitive devient plus lâche. On rencontre ainsi

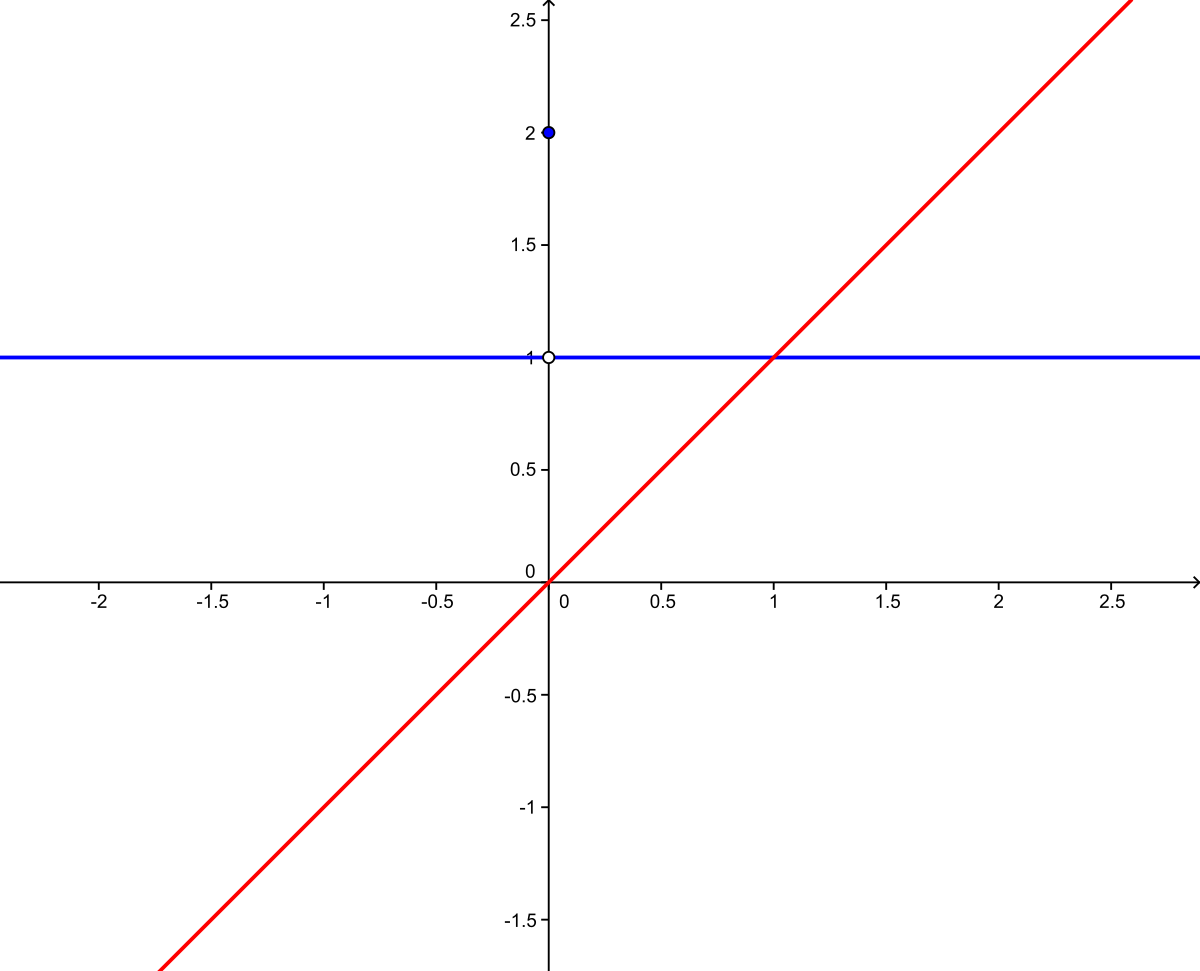
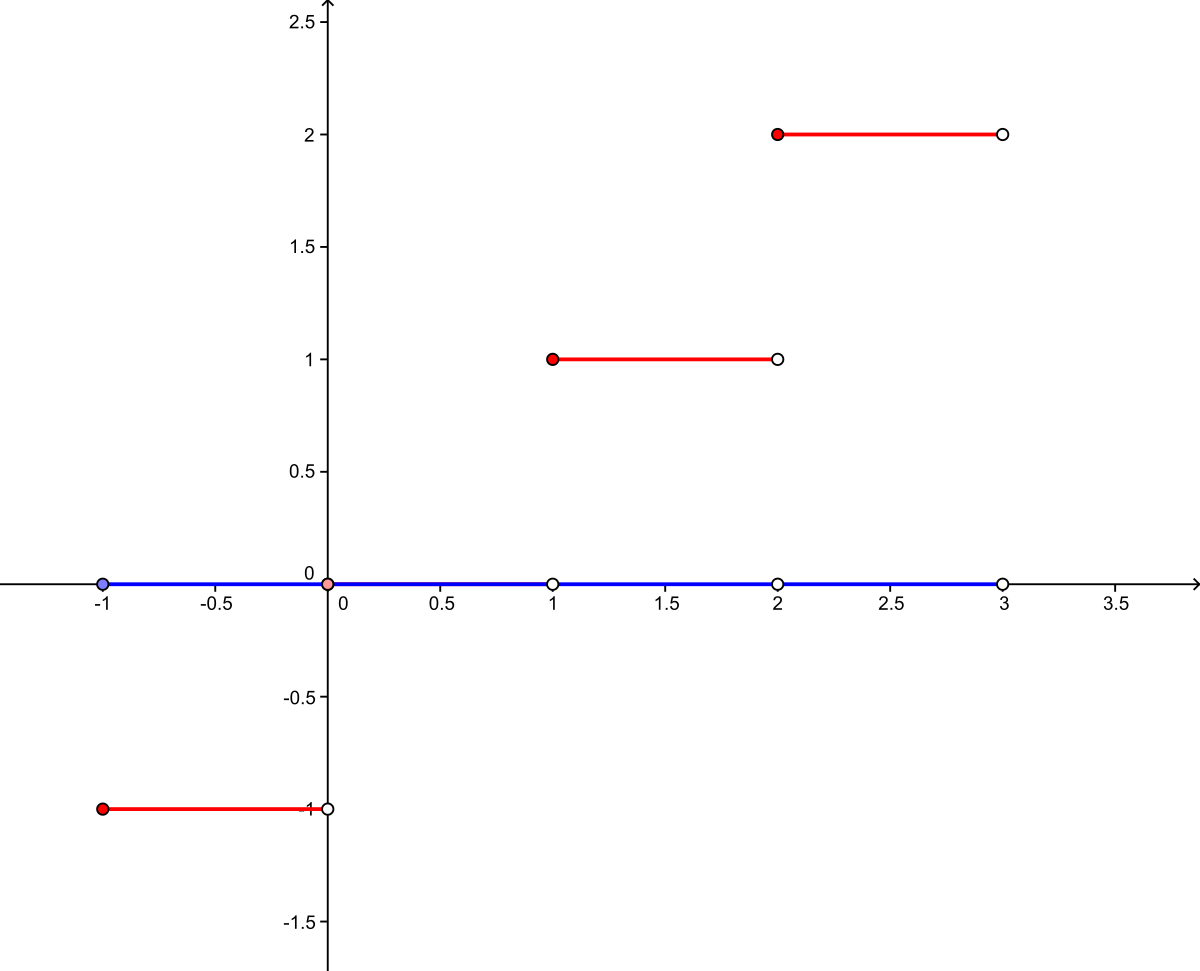
• des intégrales indéfinies non dérivables en quelques points comme celle de la fonction partie entière;
• des intégrales indéfinies dérivables sur mais dont la dérivée ne coïncide pas en tout point avec f. Il suffit de prendre par exemple la fonction constante égale à 1 sauf en x₀ où la fonction vaut 2. Son intégrale indéfinie a pour expression F(x)= x + K et la dérivée de F enx₀ vaut 1;
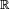
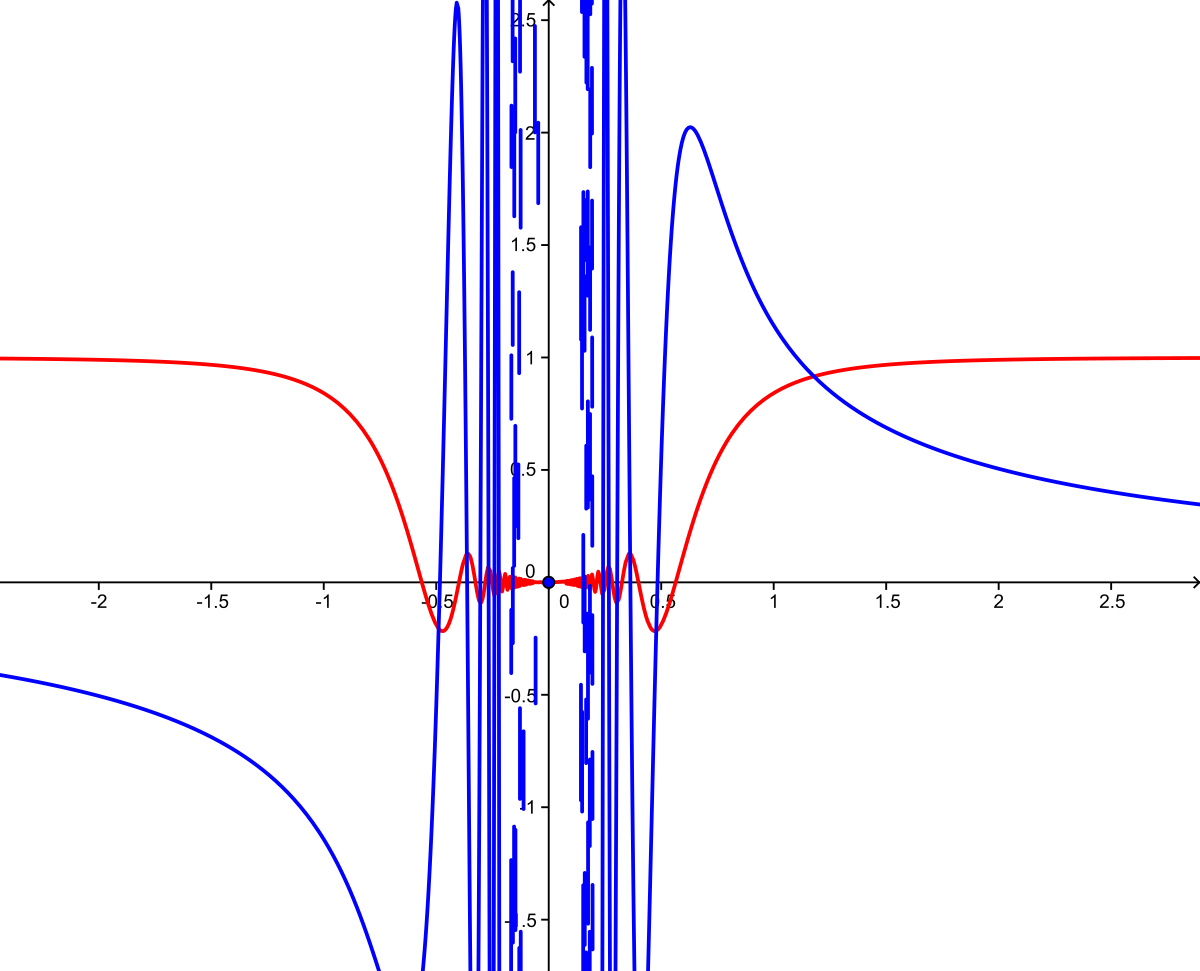
• des intégrales indéfinies qui restent non dérivables sur un ensemble dense;
• des intégrales indéfinies dérivables sur [0,1] dont la dérivée ne coïncide pas avec f sur un ensemble dense;
• des fonctions F, dérivables sauf en quelques points , mais qui ne sont pas une intégrale indéfinie de leur dérivée : par exemple, la partie entière;
• Des fonctions F, dérivables sur , mais dont la dérivée f n'est pas Riemann-intégrable donc pour laquelle on ne peut pas définir d'intégrale indéfinie. Par exemple, la fonction avec son prolongement par continuité en 0 et dérivable de dérivée non bornée donc non intégrable.

Fonction discontinue f (bleu) dont l'intégrale indéfinie F (rouge) est telle que F'(0) et f(0) sont distincts

Fonction partie entière (bleu) dont l'intégrale indéfinie (rouge) n'est pas toujours dérivable

Fonction partie entière (rouge) qui n'est pas intégrale indéfinie de sa dérivée (bleue)

Fonction x²(sin(1/x²) (rouge) dont la dérivée (bleue) n'est pas intégrable

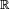
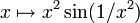
Intégrale indéfinie d'une fonction Lebesgue-intégrable

Les fonctions Lebesgue-intégrables élargissement le champ des fonctions intégrables et donc celui des intégrales indéfinies.

L'intégrale indéfinie d'une fonction Lebesgue-intégrable est absoluement continue. Réciproquement une fonction absolument continue est l'intégrale indéfinie d'une fonction Lebesgue-intégrable.

L'intégrale indéfinie d'une fonction Lebesgue-intégrable est dérivable en tout point où f est continue et F'(x)=f(x) et, plus généralement, elle est dérivable μ-presque partout de dérivée f.

Si F est dérivable sur I et de dérivée bornée alors F est une intégrale indéfinie de sa dérivée. Autrement dit, si f est bornée et possède une primitive, cette primitive correspond à une intégrale indéfinie de f.

Si F est dérivable sur I et de dérivée finie Lebesgue-intégrable alors F est une intégrale indéfinie de sa dérivée. Autrement dit, si f est Lebesgue-intégrable et possède une primitive, cette primitive correspond à une intégrale indéfinie de f.

Escalier de Cantor : fonction continue, dérivable presque partout de dérivée presque partout nulle

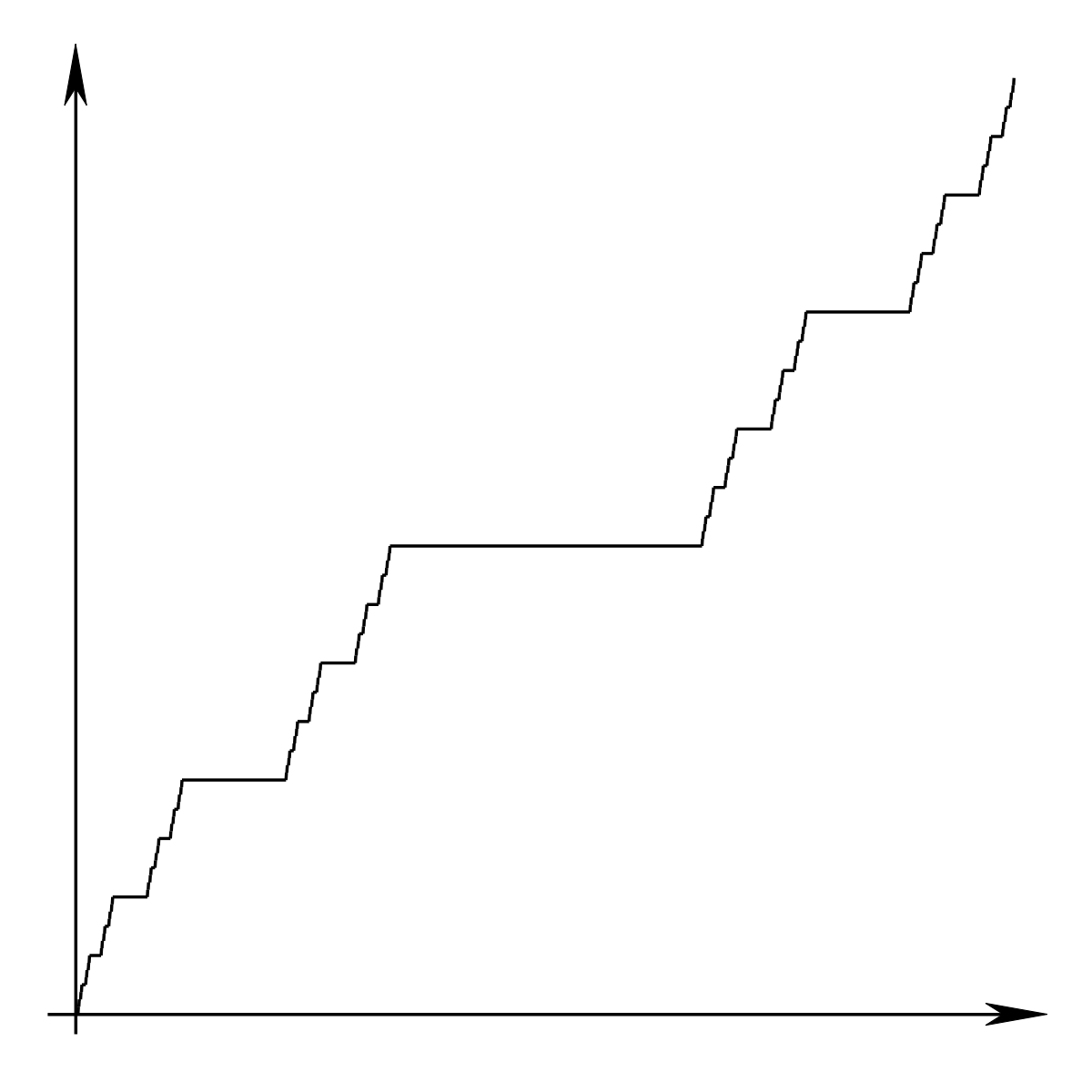
Mais il existe encore des fonctions F continues, dérivables presque partout, dont la dérivée est Lebesgue-intégrable sans pour autant que F soit une intégrale indéfinie de sa dérivée. Une exemple classique de telle fonction est l'escalier de Cantor.

Cependant, toute fonction F à variation bornée est dérivable presque partout et est la somme d'une intégrale indéfinie de F' et d'une fonction G à variation bornée de dérivée nulle μ-presque partout.

Intégrale indéfinie d'une fonction Kurzweil-Henstock-intégrable

Les fonctions KH-intégrables élargissent encore le champ des fonctions intégrables et fait coïncider presque parfaitement la notion de primitive et d'intégrale indéfinie.

Si F est dérivable sur I, alors F' est KH-intégrable et F est une intégrale indéfinie de sa dérivée. Autrement dit, si f possède des primitives, alors ce sont des intégrales indéfinies de f.

Si f est KH-intégrable sur I, alors toute intégrale indéfinie de f est continue et admet presque partout une dérivée égale à f.