Langage formel - Définition
La liste des auteurs de cet article est disponible ici.
Les langages formels, objet d'étude
Les langages formels sont aussi l'objet d'étude d'une branche à part entière de la logique et de l'informatique théorique. Cette étude est fortement liée à la théorie de la calculabilité. En effet le propre d'un langage formel, en tant que langage, c'est de pouvoir être traité par un ordinateur, ou par son modèle formel : la machine de Turing.
Définitions
En tant qu'objet d'étude, un langage formel est défini comme un ensemble de mots de longueur finie (c'est-à-dire chaînes de caractères) déduit d'un certain alphabet fini, c'est-à-dire une partie du monoïde libre sur cet alphabet.
Typiquement, un alphabet serait : {a, b}, et un mot sur cet alphabet serait : ababba.
Un langage typique sur cet alphabet, et qui contiendrait ce mot, serait l'ensemble de tous les mots qui contiennent le même nombre de symboles a et b.
Le mot vide (le mot de longueur nulle) est autorisé et est noté ε. Bien que l'alphabet soit un ensemble fini et que chaque mot ait une longueur finie, un langage peut très bien contenir une infinité de mots (parce que la longueur de ses mots peut ne pas être bornée).
Exemples
Quelques exemples de langages formels :
- l'ensemble des mots sur {a, b},
- l'ensemble { an : n est un nombre premier },
- l'ensemble des programmes syntaxiquement corrects dans un langage de programmation donné,
- l'ensemble des mots d'entrée sur lesquels une machine de Turing donnée s'arrête.
Construction d'un langage formel
Un langage formel peut être spécifié par différents moyens, comme :
- les mots produits par des règles de production dites aussi règles d'une grammaire formelle (voir classification des langages),
- les mots générés par une expression rationnelle,
- les mots acceptés par un certain automate, comme une machine de Turing ou un automate d'états finis,
- l'ensemble des instances d'un problème de décision dont la réponse est OUI,
- des résultats d'inférences.
Plusieurs opérations peuvent être utilisées pour fabriquer de nouveaux langages à partir de ceux qu'on connaît. Supposons que L1 et L2 soient des langages sur un certain alphabet commun.
- La concaténation de L1 et L2 est l'ensemble des mots de la forme vw où v est un mot de L1 et w est un mot de L2. Notation :
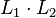
- L'intersection de L1 et L2 est l'ensemble des mots qui sont à la fois dans L1 et L2. Notation :
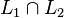
- L'union de L1 et L2 est l'ensemble des mots qui sont soit dans L1, soit dans L2. Notation :
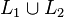
- Le complémentaire d'un langage L1 est l'ensemble des mots sur son alphabet qui ne sont pas contenus dans L1.
- Le quotient à droite de L1 et L2 est l'ensemble des mots v pour lesquels il existe un mot w de L2 tel que vw appartient à L1. Notation : L1 / L2.
- La fermeture de Kleene de L1 est l'ensemble des mots qui peuvent s'écrire
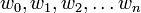
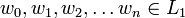
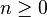
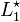
- Le renversé de L1 contient les mots de L1 écrits à l'envers. Notation :
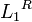
- Le mélangé de L1 et L2 est l'ensemble des mots pouvant s'écrire
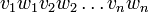
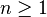
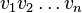
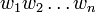
Appartenance, calculabilité et complexité
Des questions typiques que l'on se pose à propos d'un langage formel sont les suivantes:
- Peut-on décider par algorithme si un mot donné appartient à ce langage?
- Si oui, quelle est la complexité algorithmique d'une telle réponse?
Ces questions relèvent des domaines de la théorie de la calculabilité et de la théorie de la complexité.

















































