Théorie spectrale des graphes - Définition

Introduction

La théorie spectrale des graphes s'intéresse aux rapports entre le spectre d'un graphe et ses propriétés, et fait partie de la théorie algébrique des graphes. Un graphe peut-être représenté par plusieurs matrices, et les valeurs propres d'une matrice constituent son spectre. On s'intéresse en général à la matrice d'adjacence et la matrice laplacienne normalisée.

Matrices et leurs relations

Soit un graphe G = (V,E), où V dénote l'ensemble des sommets et E l'ensemble des arêtes. Le graphe possède | V | = n sommets, dénotés par et | E | = m arêtes, dénotées par . Chaque élément de la matrice d'adjacence A du graphe G est défini par :

Graphe	Représentation par une matrice d'adjacence	Représentation par une matrice laplacienne (non normalisée)

La matrice des degrés D est une matrice diagonale où les éléments D_ii correspondent au nombre de connexions du sommet i, c'est-à-dire à son degré. En utilisant cette matrice et la précédente, on peut également définir la matrice laplacienne L = D − A; on obtient sa forme normalisée L' par L' = D ^{− 1 / 2}LD ^{− 1 / 2} = I − D ^{− 1 / 2}AD ^{− 1 / 2}, où I dénote la matrice identité, ou on peut aussi l'obtenir directement par chacun de ses éléments :

Enfin, la matrice d'incidence M d'un graphe G = (V,E) est la matrice de dimensions | V | x | E | dans laquelle l'entrée b_ij vaut 1 si le sommet v_i est une extrémité de l'arête x_j, et 0 sinon. On a l'ensemble de relations suivantes, où I dénote la matrice identité :

• A = MM^T − D
• Pour la matrice d'adjacence du line graph L(G), A = M^TM − 2I
• Pour la matrice d'adjacence du graphe de subdivision S(G),

Le spectre d'une matrice est l'ensemble de ses valeurs propres ; par extension, on parle du spectre du graphe. On rappelle que la multiplicité algébrique d'une valeur propre λ est la puissance du monôme (X − λ) dans le polynôme caractéristique (i.e. la multiplicité de la racine dans le polynôme caractéristique). Il est également possible de modifier le polynôme caractéristique pour prendre en compte d'autres propriétés du graphe : on considère par défaut le polynôme P_G(λ) = | λI − A | , mais on peut aussi s'intéresser à des variantes telles que R_G(λ) = | λI − D − A | ou Q_G(λ) = | D | ^{− 1} * | λD − A | .

Spectre de la matrice laplacienne normalisée

La valeur propre λ₁ est appelée la connectivité algébrique du graphe. Les propriétés essentielles du spectre sont résumées ci-dessous :

• λ₀ = 0.
• si le graphe est connexe.
• Si et que G est un graphe complet alors , sinon .
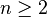
• Si le graphe est connexe alors λ₁ > 0. Si λ_i = 0 et alors G a exactement i + 1 composantes (i.e. graphes connexes).
• .

Parmi les autres propriétés de cette matrice, son déterminant donne le nombre d'arbres couvrants du graphe.

Spectre de la matrice d'adjacence

La matrice du graphe est positive, et elle ne peut être réduite si le graphe est connexe. Dans le cas d'un graphe non-orienté, la matrice est symétrique et hermitienne, c'est-à-dire que où est la matrice adjointe de A. La trace de la matrice est égale à deux fois le nombre de boucles : en effet, un élément sur la diagonale indique la présence d'une boucle et la trace est la somme de ces éléments. Nous avons les propriétés suivantes :

• Le rayon spectral ρ(A) de la matrice, c'est-à-dire sa plus grande valeur propre, satisfait pour un graphe connexe. La borne inférieure est atteinte dans le cas d'un chemin et la supérieure par un graphe complet.
• Si le graphe est k-régulier alors ρ(A) = k et la multiplicité de ρ(A) donne le nombre de composantes connexes.
• Toutes les valeurs propres sont nulles si et seulement si le graphe ne contient pas de cycle.
• Le graphe ne contient un cycle de longueur impaire que si − ρ(A) est aussi une valeur propre.
• S'il y a k valeurs propres distinctes, alors le diamètre D satisfait .
• La taille t du stable maximum satisfait où p ₋ ,p₀,p ₊ sont respectivement le nombre de valeurs propres plus petites, égales ou supérieures à 0..
• où χ(G) est le nombre chromatique et q la plus petite valeur propre.