Liste de nombres premiers - Définition
La liste des auteurs de cet article est disponible ici.
Introduction
Il existe une infinité de nombres premiers. Les 1 000 premiers sont listés ci-dessous, suivis par une liste de différents types de nombres premiers.
Mille premiers nombres premiers
2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59, 61, 67, 71, 73, 79, 83, 89, 97, 101, 103, 107, 109, 113, 127, 131, 137, 139, 149, 151, 157, 163, 167, 173, 179, 181, 191, 193, 197, 199, 211, 223, 227, 229, 233, 239, 241, 251, 257, 263, 269, 271, 277, 281, 283, 293, 307, 311, 313, 317, 331, 337, 347, 349, 353, 359, 367, 373, 379, 383, 389, 397, 401, 409, 419, 421, 431, 433, 439, 443, 449, 457, 461, 463, 467, 479, 487, 491, 499, 503, 509, 521, 523, 541, 547, 557, 563, 569, 571, 577, 587, 593, 599, 601, 607, 613, 617, 619, 631, 641, 643, 647, 653, 659, 661, 673, 677, 683, 691, 701, 709, 719, 727, 733, 739, 743, 751, 757, 761, 769, 773, 787, 797, 809, 811, 821, 823, 827, 829, 839, 853, 857, 859, 863, 877, 881, 883, 887, 907, 911, 919, 929, 937, 941, 947, 953, 967, 971, 977, 983, 991, 997, 1009, 1013, 1019, 1021, 1031, 1033, 1039, 1049, 1051, 1061, 1063, 1069, 1087, 1091, 1093, 1097, 1103, 1109, 1117, 1123, 1129, 1151, 1153, 1163, 1171, 1181, 1187, 1193, 1201, 1213, 1217, 1223, 1229, 1231, 1237, 1249, 1259, 1277, 1279, 1283, 1289, 1291, 1297, 1301, 1303, 1307, 1319, 1321, 1327, 1361, 1367, 1373, 1381, 1399, 1409, 1423, 1427, 1429, 1433, 1439, 1447, 1451, 1453, 1459, 1471, 1481, 1483, 1487, 1489, 1493, 1499, 1511, 1523, 1531, 1543, 1549, 1553, 1559, 1567, 1571, 1579, 1583, 1597, 1601, 1607, 1609, 1613, 1619, 1621, 1627, 1637, 1657, 1663, 1667, 1669, 1693, 1697, 1699, 1709, 1721, 1723, 1733, 1741, 1747, 1753, 1759, 1777, 1783, 1787, 1789, 1801, 1811, 1823, 1831, 1847, 1861, 1867, 1871, 1873, 1877, 1879, 1889, 1901, 1907, 1913, 1931, 1933, 1949, 1951, 1973, 1979, 1987, 1993, 1997, 1999, 2003, 2011, 2017, 2027, 2029, 2039, 2053, 2063, 2069, 2081, 2083, 2087, 2089, 2099, 2111, 2113, 2129, 2131, 2137, 2141, 2143, 2153, 2161, 2179, 2203, 2207, 2213, 2221, 2237, 2239, 2243, 2251, 2267, 2269, 2273, 2281, 2287, 2293, 2297, 2309, 2311, 2333, 2339, 2341, 2347, 2351, 2357, 2371, 2377, 2381, 2383, 2389, 2393, 2399, 2411, 2417, 2423, 2437, 2441, 2447, 2459, 2467, 2473, 2477, 2503, 2521, 2531, 2539, 2543, 2549, 2551, 2557, 2579, 2591, 2593, 2609, 2617, 2621, 2633, 2647, 2657, 2659, 2663, 2671, 2677, 2683, 2687, 2689, 2693, 2699, 2707, 2711, 2713, 2719, 2729, 2731, 2741, 2749, 2753, 2767, 2777, 2789, 2791, 2797, 2801, 2803, 2819, 2833, 2837, 2843, 2851, 2857, 2861, 2879, 2887, 2897, 2903, 2909, 2917, 2927, 2939, 2953, 2957, 2963, 2969, 2971, 2999, 3001, 3011, 3019, 3023, 3037, 3041, 3049, 3061, 3067, 3079, 3083, 3089, 3109, 3119, 3121, 3137, 3163, 3167, 3169, 3181, 3187, 3191, 3203, 3209, 3217, 3221, 3229, 3251, 3253, 3257, 3259, 3271, 3299, 3301, 3307, 3313, 3319, 3323, 3329, 3331, 3343, 3347, 3359, 3361, 3371, 3373, 3389, 3391, 3407, 3413, 3433, 3449, 3457, 3461, 3463, 3467, 3469, 3491, 3499, 3511, 3517, 3527, 3529, 3533, 3539, 3541, 3547, 3557, 3559, 3571, 3581, 3583, 3593, 3607, 3613, 3617, 3623, 3631, 3637, 3643, 3659, 3671, 3673, 3677, 3691, 3697, 3701, 3709, 3719, 3727, 3733, 3739, 3761, 3767, 3769, 3779, 3793, 3797, 3803, 3821, 3823, 3833, 3847, 3851, 3853, 3863, 3877, 3881, 3889, 3907, 3911, 3917, 3919, 3923, 3929, 3931, 3943, 3947, 3967, 3989, 4001, 4003, 4007, 4013, 4019, 4021, 4027, 4049, 4051, 4057, 4073, 4079, 4091, 4093, 4099, 4111, 4127, 4129, 4133, 4139, 4153, 4157, 4159, 4177, 4201, 4211, 4217, 4219, 4229, 4231, 4241, 4243, 4253, 4259, 4261, 4271, 4273, 4283, 4289, 4297, 4327, 4337, 4339, 4349, 4357, 4363, 4373, 4391, 4397, 4409, 4421, 4423, 4441, 4447, 4451, 4457, 4463, 4481, 4483, 4493, 4507, 4513, 4517, 4519, 4523, 4547, 4549, 4561, 4567, 4583, 4591, 4597, 4603, 4621, 4637, 4639, 4643, 4649, 4651, 4657, 4663, 4673, 4679, 4691, 4703, 4721, 4723, 4729, 4733, 4751, 4759, 4783, 4787, 4789, 4793, 4799, 4801, 4813, 4817, 4831, 4861, 4871, 4877, 4889, 4903, 4909, 4919, 4931, 4933, 4937, 4943, 4951, 4957, 4967, 4969, 4973, 4987, 4993, 4999, 5003, 5009, 5011, 5021, 5023, 5039, 5051, 5059, 5077, 5081, 5087, 5099, 5101, 5107, 5113, 5119, 5147, 5153, 5167, 5171, 5179, 5189, 5197, 5209, 5227, 5231, 5233, 5237, 5261, 5273, 5279, 5281, 5297, 5303, 5309, 5323, 5333, 5347, 5351, 5381, 5387, 5393, 5399, 5407, 5413, 5417, 5419, 5431, 5437, 5441, 5443, 5449, 5471, 5477, 5479, 5483, 5501, 5503, 5507, 5519, 5521, 5527, 5531, 5557, 5563, 5569, 5573, 5581, 5591, 5623, 5639, 5641, 5647, 5651, 5653, 5657, 5659, 5669, 5683, 5689, 5693, 5701, 5711, 5717, 5737, 5741, 5743, 5749, 5779, 5783, 5791, 5801, 5807, 5813, 5821, 5827, 5839, 5843, 5849, 5851, 5857, 5861, 5867, 5869, 5879, 5881, 5897, 5903, 5923, 5927, 5939, 5953, 5981, 5987, 6007, 6011, 6029, 6037, 6043, 6047, 6053, 6067, 6073, 6079, 6089, 6091, 6101, 6113, 6121, 6131, 6133, 6143, 6151, 6163, 6173, 6197, 6199, 6203, 6211, 6217, 6221, 6229, 6247, 6257, 6263, 6269, 6271, 6277, 6287, 6299, 6301, 6311, 6317, 6323, 6329, 6337, 6343, 6353, 6359, 6361, 6367, 6373, 6379, 6389, 6397, 6421, 6427, 6449, 6451, 6469, 6473, 6481, 6491, 6521, 6529, 6547, 6551, 6553, 6563, 6569, 6571, 6577, 6581, 6599, 6607, 6619, 6637, 6653, 6659, 6661, 6673, 6679, 6689, 6691, 6701, 6703, 6709, 6719, 6733, 6737, 6761, 6763, 6779, 6781, 6791, 6793, 6803, 6823, 6827, 6829, 6833, 6841, 6857, 6863, 6869, 6871, 6883, 6899, 6907, 6911, 6917, 6947, 6949, 6959, 6961, 6967, 6971, 6977, 6983, 6991, 6997, 7001, 7013, 7019, 7027, 7039, 7043, 7057, 7069, 7079, 7103, 7109, 7121, 7127, 7129, 7151, 7159, 7177, 7187, 7193, 7207, 7211, 7213, 7219, 7229, 7237, 7243, 7247, 7253, 7283, 7297, 7307, 7309, 7321, 7331, 7333, 7349, 7351, 7369, 7393, 7411, 7417, 7433, 7451, 7457, 7459, 7477, 7481, 7487, 7489, 7499, 7507, 7517, 7523, 7529, 7537, 7541, 7547, 7549, 7559, 7561, 7573, 7577, 7583, 7589, 7591, 7603, 7607, 7621, 7639, 7643, 7649, 7669, 7673, 7681, 7687, 7691, 7699, 7703, 7717, 7723, 7727, 7741, 7753, 7757, 7759, 7789, 7793, 7817, 7823, 7829,
7841, 7853, 7867, 7873, 7877, 7879, 7883, 7901, 7907, 7919Auto premier
Premier ne pouvant pas s'écrire sous la forme d'un nombre ajouté à la somme des chiffres de ce nombre. En base 10 :
3, 5, 7, 31, 53, 97, 211, 233, 277, 367, 389, 457, 479
Bell
Premier égal au nombre de partitions d'un ensemble de n membres.
2, 5, 877, 27644437, 35742549198872617291353508656626642567, 359334085968622831041960188598043661065388726959079837
Carol
Premier de la forme (2n - 1)² - 2.
7, 47, 223, 3967, 16127, 1046527, 16769023, 1073676287, 68718952447
Carré centré
Premier de la forme n² + (n + 1)².
5, 13, 41, 61, 113, 181, 313, 421, 613, 761, 1013, 1201, 1301, 1741, 1861, 2113, 2381, 2521, 3121, 3613
Chanceux
Nombre chanceux également premier.
3, 7, 13, 31, 37, 43, 67, 73, 79, 127, 151, 163, 193, 211, 223, 241, 283, 307, 331, 349, 367, 409, 421, 433, 463, 487, 541, 577, 601, 613, 619, 631, 643, 673, 727, 739, 769, 787, 823, 883, 937, 991, 997, 1009, 1021, 1039, 1087, 1093, 1117, 1123, 1201, 1231, 1249, 1291, 1303, 1459, 1471, 1543, 1567, 1579, 1597, 1663, 1693, 1723, 1777, 1801, 1831, 1879, 1933, 1987, 2053, 2083, 2113, 2221, 2239, 2251, 2281, 2311, 2467, 2473, 2557, 2593, 2647, 2671, 2689, 2797, 2851, 2887, 2953, 2971, 3037, 3049, 3109, 3121, 3163, 3187, 3229, 3259, 3301, 3307, 3313
Chen
Premier p tel que p + 2 est soit premier, soit semi-premier.
2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 47, 53, 59, 67, 71, 83, 89, 101, 107, 109, 113, 127, 131, 137, 139, 149, 157, 167, 179, 181, 191, 197, 199, 211, 227, 233, 239, 251, 257, 263, 269, 281, 293, 307, 311, 317, 337, 347, 353, 359, 379, 389, 401, 409, 419, 431, 443, 449, 461, 467, 479, 487, 491, 499
Cousins
Paire de nombres premiers de la forme (p, p + 4).
(3, 7), (7, 11), (13, 17), (19, 23), (37, 41), (43, 47), (67, 71), (79, 83), (97, 101), (103, 107), (109, 113), (127, 131), (163, 167), (193, 197), (223, 227), (229, 233), (277, 281), (307, 311), (313, 317), (349, 353), (379, 383), (397, 401), [Faux](439, 441), (457, 461), (487, 491), (499, 503), (613, 617), (643, 647), (673, 677), (739, 743), (757, 761), (769, 773), (823, 827), (853, 857), (859, 863), (877, 881), (883, 887), (907, 911), (937, 941), (967, 971), (1009, 1013), (1087, 1091)
Cubain
Premier de la forme (x3 - y3) , avec x = y + 1 :
7, 19, 37, 61, 127, 271, 331, 397, 547, 631, 919, 1657, 1801, 1951, 2269, 2437, 2791, 3169, 3571, 4219, 4447, 5167, 5419, 6211, 7057, 7351, 8269, 9241, 10267, 11719, 12097, 13267, 13669, 16651, 19441, 19927, 22447, 23497, 24571, 25117, 26227
Premier de la forme (x3 - y3) / (x - y), avec x = y + 2 :
13, 109, 193, 433, 769, 1201, 1453, 2029, 3469, 3889, 4801, 10093, 12289, 13873, 18253, 20173, 21169, 22189, 28813, 37633, 43201, 47629, 60493, 63949, 65713, 69313
Cullen
Premier de la forme n × 2n + 1.
3, 393050634124102232869567034555427371542904833
Décagonal centré
Premier de la forme 5(n² - n) + 1.
11, 31, 61, 101, 151, 211, 281, 661, 911, 1051, 1201, 1361, 1901, 2311, 2531, 3001, 3251, 3511, 4651, 5281
Double de Mersenne
Premier de la forme 2(2p - 1) - 1, p premier.
7, 127, 2147483647, 170141183460469231731687303715884105727
Eisenstein
Entier d'Eisenstein irréductibles et réels.
2, 3, 7, 5, 11, 17, 23, 29, 41, 47, 53, 59, 71, 83, 89, 101, 107, 113, 131, 137, 149, 167, 173, 179, 191, 197, 227, 233, 239, 251, 257, 263, 269, 281, 293, 311, 317, 347, 353, 359, 383, 389, 401, 419, 431, 443, 449, 461, 467, 479, 491
Équilibré
Nombre premier à égale distance des premiers précédent et suivant.
5, 53, 157, 173, 211, 257, 263, 373, 563, 593, 607, 653, 733, 947, 977, 1103
Étoilé
Premier de la forme 6n(n - 1) + 1.
13, 37, 73, 181, 337, 433, 541, 661, 937, 1093, 2053, 2281, 2521, 3037, 3313
Euclide
Premier de la forme pn# + 1.
3, 7, 31, 211, 2311
Factoriel
Premier de la forme n! - 1 ou n! + 1.
2, 3, 5, 7, 23, 719, 5039, 39916801, 479001599, 87178291199
Fermat
Premier de la forme 22n + 1.
3, 5, 17, 257, 65537
Fibonacci
Premiers dans la suite de Fibonacci.
2, 3, 5, 13, 89, 233, 1597, 28657, 514229, 433494437, 2971215073
Gauss
Entier de Gauss premier.
3, 7, 11, 19, 23, 31, 43, 47, 59, 67, 71, 79, 83, 103, 107, 127, 131, 139, 151, 163, 167, 179, 191, 199, 211, 223, 227, 239, 251, 263, 271, 283, 307, 311, 331, 347, 359, 367, 379, 383, 419, 431, 439, 443, 463, 467, 479, 487, 491, 499
Genocchi
17
Le seul nombre de Genocchi premier est 17 (et -3 si les nombres premiers négatifs sont inclus).
Heureux
Nombre heureux premier
7, 13, 19, 23, 31, 79, 97, 103, 109, 139, 167, 193, 239, 263, 293, 313, 331, 367, 379, 383, 397, 409, 487, 563
Higgs
Premier p pour qui p - 1 divise le carré du produit de tous les nombres premiers de Higgs inférieurs.
2, 3, 5, 7, 11, 13, 19, 23, 29, 31, 37, 43, 47, 53, 59, 61, 67, 71, 79, 101, 107, 127, 131, 139, 149, 151, 157, 173, 181, 191, 197, 199, 211, 223, 229, 263, 269, 277, 283, 311, 317, 331, 347, 349
Heptagonal centré
Premier de la forme (7n² - 7n + 2) / 2.
43, 71, 197, 463, 547, 953, 1471, 1933, 2647, 2843
Impair
Premier de la forme 2n + 1.
3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59, 61, 67, 71, 73, 79, 83, 89, 97
Il s'agit de l'ensemble des nombres premiers à l'exception de 2.
Irrégulier
Nombre premier impair p qui divise la nombre de classes de l'ensemble des racines pième de l'unité.
37, 59, 67, 101, 103, 131, 149, 157, 233, 257, 263, 271, 283, 293, 307, 311, 347, 353, 379, 389, 401, 409, 421, 433, 461, 463, 467, 491
Jumeaux
Paire de nombres premiers de la forme (p, p + 2).
(3, 5), (5, 7), (11, 13), (17, 19), (29, 31), (41, 43), (59, 61), (71, 73), (101, 103), (107, 109), (137, 139), (149, 151), (179, 181), (191, 193), (197, 199), (227, 229), (239, 241), (269, 271), (281, 283), (311, 313), (347, 349), (419, 421), (431, 433), (461, 463), (521, 523), (569, 571), (599, 601), (617, 619), (641, 643), (659, 661), (809, 811), (821, 823), (827, 829), (857, 859), (881, 883), (1019, 1021), (1031, 1033), (1049, 1051), (1061, 1063), (1091, 1093), (1151, 1153), (1229, 1231), (1277, 1279), (1289, 1291), (1301, 1303), (1319, 1321), (1427, 1429), (1451, 1453), (1481, 1483), (1487, 1489), (1607, 1609), (1619, 1621), (1667, 1669), (1697, 1699), (1721, 1723), (1787, 1789), (1871, 1873), (1877, 1879), (1931, 1933), (1949, 1951), (1997, 1999), (2027, 2029), (2081, 2083), (2087, 2089), (2111, 2113), (2129, 2131), (2141, 2143), (2237, 2239), (2267, 2269), (2309, 2311), (2339, 2341), (2381, 2383)
Kynea
Premier de la forme (2n + 1)² - 2.
7, 23, 79, 1087, 66047, 263167, 16785407, 1073807359
Leyland
Premier de la forme xy + yx avec 1 < x ≤ y.
17, 593, 32993, 2097593
Long
Premier p pour qui, pour une base b donnée, (bp - 1 - 1)/p donne un nombre cyclique. Pour la base 10 :
7, 17, 19, 23, 29, 47, 59, 61, 97, 109, 113, 131, 149, 167, 179, 181, 193, 223, 229, 233, 257, 263, 269, 313, 337, 367, 379, 383, 389, 419, 433, 461, 487, 491, 499
Lucas
Premier dans la suite de Lucas L0 = 2, L1 = 1, Ln = Ln - 1 + Ln - 2.
2, 3, 7, 11, 29, 47, 199, 521, 2207, 3571, 9349
Markov
Premier p pour qui existent des entiers x et y tels que x² + y² + p² = 3xyp.
2, 5, 13, 29, 89, 233, 433, 1597, 2897
Mersenne
Premier de la forme 2n - 1. Remarque : Dans leur représentation en base 2, ils sont des répunits.
3, 7, 31, 127, 8191, 131071, 524287, 2147483647, 2305843009213693951, 618970019642690137449562111, 162259276829213363391578010288127, 170141183460469231731687303715884105727
Mills
Premier de la forme
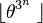
2, 11, 1361, 2521008887, 16022236204009818131831320183
Motzkin
Premier égal au nombre de façon différentes de dessiner des cordes non-sécantes entre n points d'un cercle.
2, 127, 15511, 953467954114363
Newman-Shanks-Williams
Nombre de Newman-Shanks-Williams premier.
7, 41, 239, 9369319, 63018038201, 489133282872437279, 19175002942688032928599
Padovan
Premier dans la suite de Padovan P(0)=P(1)=P(2)=1, P(n)=P(n - 2) + P(n - 3).
2, 3, 5, 7, 37, 151, 3329, 23833
Pair
Premier de la forme 2n.
2
Le seul nombre premier pair est 2. Tous les autres sont impairs.
Palindrome
Premier restant lui-même quand ses chiffres sont lus à l'envers.
2, 3, 5, 7, 11, 101, 131, 151, 181, 191, 313, 353, 373, 383, 727, 757, 787, 797, 919, 929, 10301, 10501, 10601, 11311, 11411, 12421, 12721, 12821, 13331, 13831, 13931, 14341, 14741, 15451, 15551, 16061, 16361, 16561, 16661, 17471, 17971, 18181, 18481, 19391, 19891, 19991
Pell
Premier dans la suite de Pell P0 = 0, P1 = 1, Pn = 2Pn - 1 + Pn - 2.
2, 5, 29, 5741, 33461
Permutable
Toute permutation des chiffres est première.
2, 3, 5, 7, 11, 13, 17, 31, 37, 71, 73, 79, 97, 113, 131, 199, 311, 337, 373, 733, 919, 991, 1111111111111111111, 11111111111111111111111
Perrin
Premier dans la suite de Perrin P(0) = 3, P(1) = 0, P(2) = 2, P(n) = P(n - 2) + P(n - 3).
2, 3, 5, 7, 17, 29, 277, 367, 853
Pierpont
Premier de la forme 2u 3v + 1 pour deux entiers u,v ≥ 0.
2, 3, 5, 7, 13, 17, 19, 37, 73, 97, 109, 163, 193, 257, 433, 487, 577, 769, 1153, 1297, 1459, 2593, 2917, 3457, 3889, 10369, 12289, 17497, 18433, 39367, 52489, 65537, 139969, 147457, 209953, 331777, 472393, 629857, 746497, 786433, 839809, 995329
Pillai
Premier p pour qui existe n > 0 tel que p divise n! + 1 et n ne divise pas p - 1.
23, 29, 59, 61, 67, 71, 79, 83, 109, 137, 139, 149, 193
Primoriel
Premier de la forme pn# - 1 ou pn# + 1.
5, 7, 29, 31, 211, 2309, 2311, 30029
Proth
Premier de la forme k × 2n + 1 avec k pair et k < 2n.
3, 5, 13, 17, 41, 97, 113, 193, 241, 257, 353, 449, 577, 641, 673, 769, 929, 1153
Pythagore
Premier de la forme 4n + 1.
5, 13, 17, 29, 37, 41, 53, 61, 73, 89, 97, 101, 109, 113, 137, 149, 157, 173, 181, 193, 197, 229, 233, 241, 257, 269, 277, 281, 293, 313, 317, 337, 349, 353, 373, 389, 397, 401, 409, 421, 433, 449, 457, 461
Quadruplet de nombres premiers
Quadruplet de la forme (p, p + 2, p + 6, p + 8) dont tous les membres sont premiers.
(5, 7, 11, 13), (11, 13, 17, 19), (101, 103, 107, 109), (191, 193, 197, 199), (821, 823, 827, 829), (1481, 1483, 1487, 1489), (1871, 1873, 1877, 1879), (2081, 2083, 2087, 2089), (3251, 3253, 3257, 3259), (3461, 3463, 3467, 3469), (5651, 5653, 5657, 5659), (9431, 9433, 9437, 9439), (13001, 13003, 13007, 13009), (15641, 15643, 15647, 15649), (15731, 15733, 15737, 15739), (16061, 16063, 16067, 16069), (18041, 18043, 18047, 18049), (18911, 18913, 18917, 18919), (19421, 19423, 19427, 19429), (21011, 21013, 21017, 21019), (22271, 22273, 22277, 22279), (25301, 25303, 25307, 25309), (31721, 31723, 31727, 31729), (34841, 34843, 34847, 34849), (43781, 43783, 43787, 43789), (51341, 51343, 51347, 51349), (55331, 55333, 55337, 55339), (62981, 62983, 62987, 62989), (67211, 67213, 67217, 67219), (69491, 69493, 69497, 69499), (72221, 72223, 72227, 72229), (77261, 77263, 77267, 77269), (79691, 79693, 79697, 79699), (81041, 81043, 81047, 81049), (82721, 82723, 82727, 82729), (88811, 88813, 88817, 88819), (97841, 97843, 97847, 97849), (99131, 99133, 99137, 99139)
Ramanujan
2, 11, 17, 29, 41, 47, 59, 67, 71, 97, 101, 107, 127, 149, 151, 167, 179, 181, 227, 229, 233, 239, 241, 263, 269, 281, 307, 311, 347, 349, 367, 373, 401, 409, 419, 431, 433, 439, 461, 487, 491
Régulier
Nombre premier p ne divisant pas le nombre de classes de l'ensemble des racines pième de l'unité.
3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 41, 43, 47, 53, 61, 71, 73, 79, 83, 89, 97, 107, 109, 113, 127, 137, 139, 151, 163, 167, 173, 179, 181, 191, 193, 197, 199, 211, 223, 227, 229, 239, 241, 251, 269, 277, 281, 313, 317, 331, 337, 349, 359, 367, 373, 383, 397, 401
Reimerp
Premier devenant un premier distinct lorsque ses chiffres sont inversés.
13, 17, 31, 37, 71, 73, 79, 97, 107, 113, 149, 157
Répunit
Premier ne contenant que des chiffres 1.
11, 1111111111111111111, 11111111111111111111111
Sûr
p et (p - 1) / 2 sont premiers.
5, 7, 11, 23, 47, 59, 83, 107, 167, 179, 227, 263, 347, 359, 383, 467, 479, 503, 563, 587, 719, 839, 863, 887, 983, 1019, 1187, 1283, 1307, 1319, 1367, 1439, 1487, 1523, 1619, 1823, 1907
Sexy
p et p + 6 sont premiers.
(5,11), (7,13), (11,17), (13,19), (17,23), (23,29), (31,37), (37,43), (41,47), (47,53), (53,59), (61,67), (67,73), (73,79), (83,89), (97,103), (101,107), (103,109), (107,113), (131,137), (151,157), (157,163), (167,173), (173,179), (191,197), (193,199), (223,229), (227,233), (233,239), (251,257), (263,269), (271,277), (277,283), (307,313), (311,317), (331,337), (347,353), (353,359), (367,373), (373,379), (383,389), (433,439), (443,449), (457,463), (461,467), (503,509)
Smarandache-Wellin
Premiers égaux à la concaténation des n premiers nombres premiers écrits en base 10.
2, 23, 2357
Sophie Germain
p et 2p + 1 sont premiers.
2, 3, 5, 11, 23, 29, 41, 53, 59, 83, 89, 113, 131, 173, 179, 191, 233, 239, 251, 281, 293, 359, 419, 431, 443, 491, 509, 593, 641, 653, 659, 683, 719, 743, 761, 809, 911, 953, 1013, 1019, 1031, 1049, 1103, 1223, 1229, 1289, 1409, 1439, 1451, 1481, 1499, 1511,1559
Stern
Premier n'étant pas la somme d'un nombre premier plus petit et de deux fois le carré d'un entier non-nul.
2, 3, 17, 137, 227, 977, 1187, 1493
Supersingulier
2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 41, 47, 59, 71
Thabit
Premier de la forme 3 · 2n - 1. Remarque : Dans leur représentation en base 2, ces nombres sont tous de la forme "10111...111" (un 1, un 0, suivis de un ou plusieurs 1)
2, 5, 11, 23, 47, 191, 383, 6143
Triangulaire centré
Premier de la forme (3n² + 3n + 2) / 2.
19, 31, 109, 199, 409, 571, 631, 829, 1489, 1999, 2341, 2971
Triplet de nombres premiers
Triplet de la forme (p, p + 2, p + 6) ou (p, p + 4, p + 6) dont tous les membres sont premiers.
(5, 7, 11), (7, 11, 13), (11, 13, 17), (13, 17, 19), (17, 19, 23), (37, 41, 43), (41, 43, 47), (67, 71, 73), (97, 101, 103), (101, 103, 107), (103, 107, 109), (107, 109, 113), (191, 193, 197), (193, 197, 199), (223, 227, 229), (227, 229, 233), (277, 281, 283), (307, 311, 313), (311, 313, 317), (347, 349, 353), (457, 461, 463), (461, 463, 467), (613, 617, 619), (641, 643, 647), (821, 823, 827), (823, 827, 829), (853, 857, 859), (857, 859, 863), (877, 881, 883), (881, 883, 887)
Tronquable à droite
Premier le restant lorsque ses derniers chiffres sont successivement enlevés.
23, 29, 31, 37, 53, 59, 71, 73, 79, 233, 239... Le plus grand nombre premier troncable à droite est 73 939 133.
Tronquable à gauche
Premier le restant lorsque ses premiers chiffres sont successivement enlevés.
13, 17, 23, 37, 43, 47, 53, 67, 73, 83, 97, 113... Le plus grand nombre premier tronquable à gauche est 357 686 312 646 216 567 629 137.
Unique
Premierp pour qui la longueur de la période du développement décimal de 1 / p est unique (aucun autre premier ne donne la même).
3, 11, 37, 101, 9091, 9901, 333667
Wagstaff
Premier de la forme (2n + 1) / 3. Remarque : Dans leur représentation en base 2, ces nombres sont tous de la forme "1010...1011" (une succession de 1 et de 0 se terminant par 11).
3, 11, 43, 683, 2731, 43691, 174763, 2796203
Wedderburn-Etherington
Nombre de Wedderburn-Etherington premier.
2, 3, 11, 23, 983, 2179, 24631, 3626149
Wieferich
Premier p tel que p² divise 2p - 1 - 1
1093, 3511
Wilson
Premier p pour qui p² divise (p - 1)! + 1
5, 13, 563
Wolstenholme
Premier p pour qui le Coefficient binomial
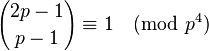
16843, 2124679
Woodall
Premier de la forme n · 2n - 1.
7, 23, 383, 32212254719, 2833419889721787128217599

















































