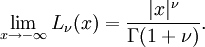Loi de Rice - Définition
La liste des auteurs de cet article est disponible ici.
Introduction
En statistiques et théorie des probabilités, la loi de Rice est une loi statistique continue (c'est-à-dire à densité).
C'est une généralisation de la loi de Rayleigh utilisée pour décrire le comportement d'un signal radio qui se propage selon plusieurs chemins (multipath) avant d'être reçu par une antenne.
| Rice | |
|---|---|
| |
| |
| | |
| Paramètres |
|
| Support |
|
| Densité de probabilité (fonction de masse) |
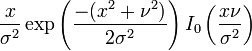
|
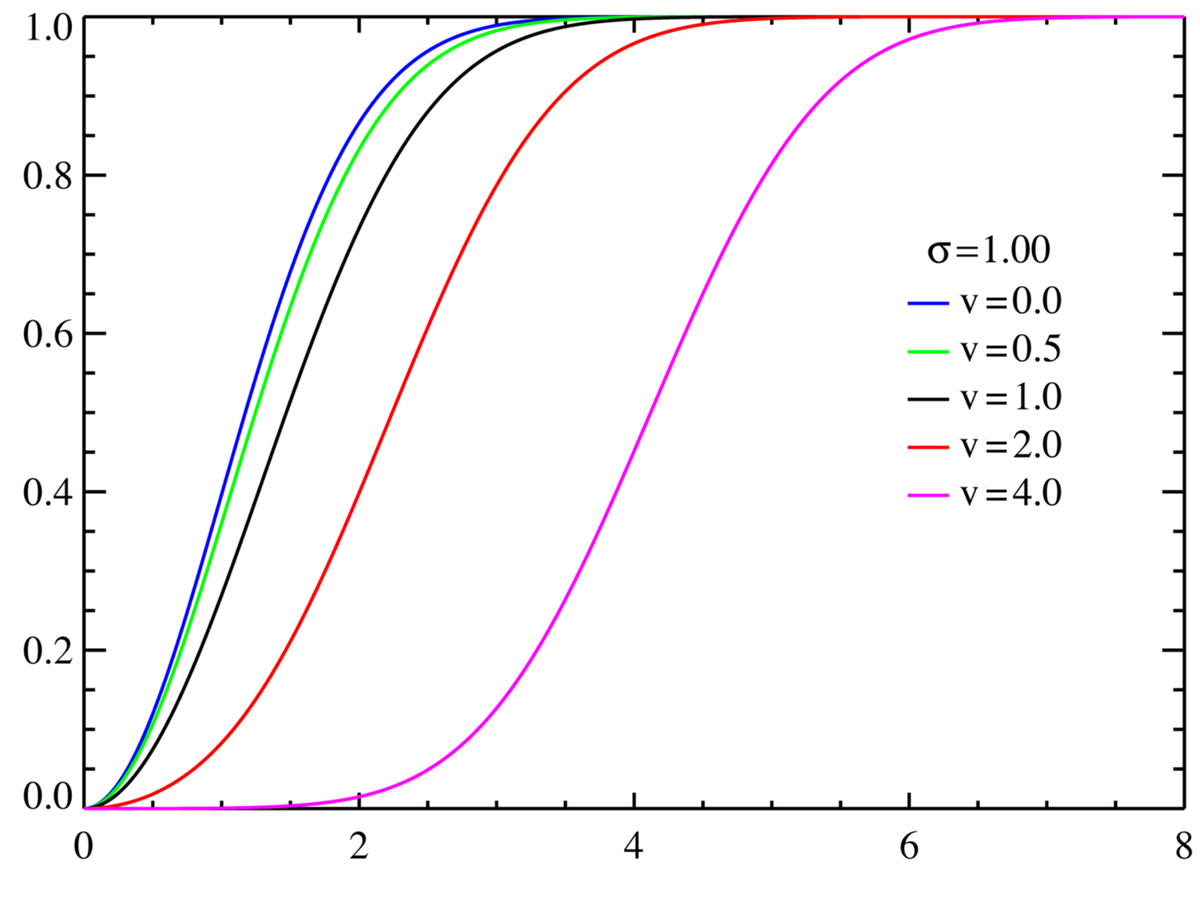
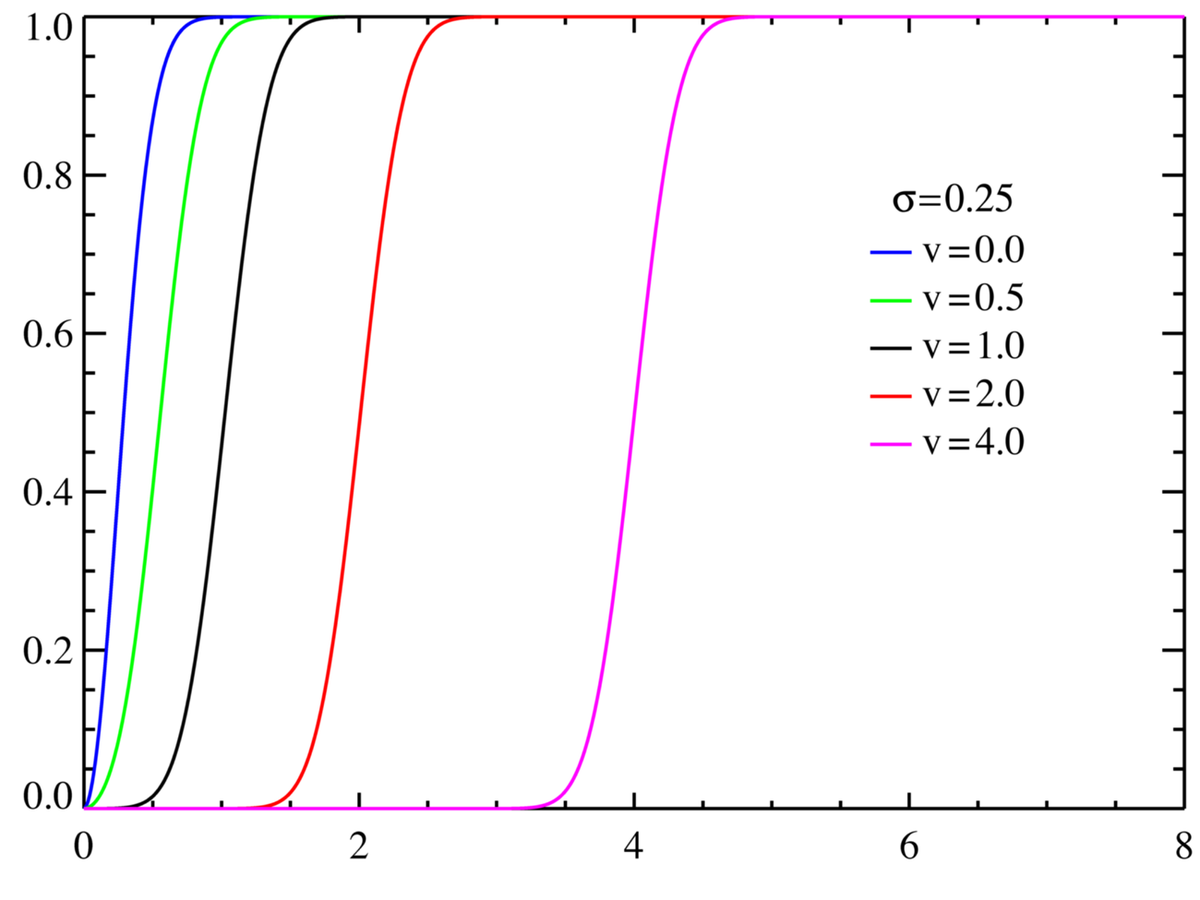
| Fonction de répartition |
où Q1 is the Marcum Q-Function |
| Espérance |
|
| Variance |
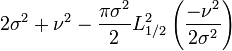
|
| Asymétrie (statistique) | (compliqué) |
| Kurtosis (non-normalisé) | (compliqué) |
| modifier | |
Caractérisation
Soient deux variables de Gauss centrées, indépendantes, de même variance σ2. Si on considère qu'elles représentent les deux coordonnées d'un point d'un plan, la distance de ce point à l'origine suit une loi de Rayleigh :
-
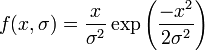
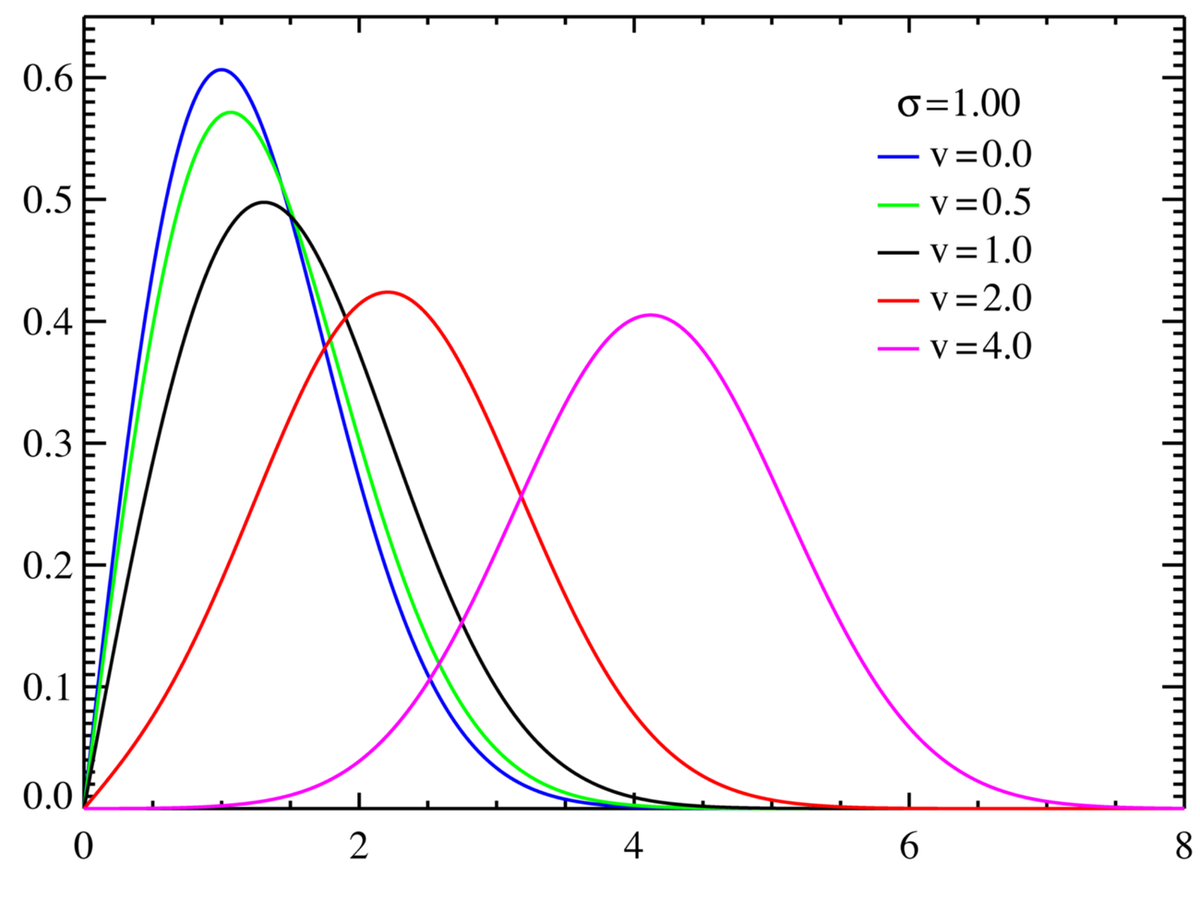
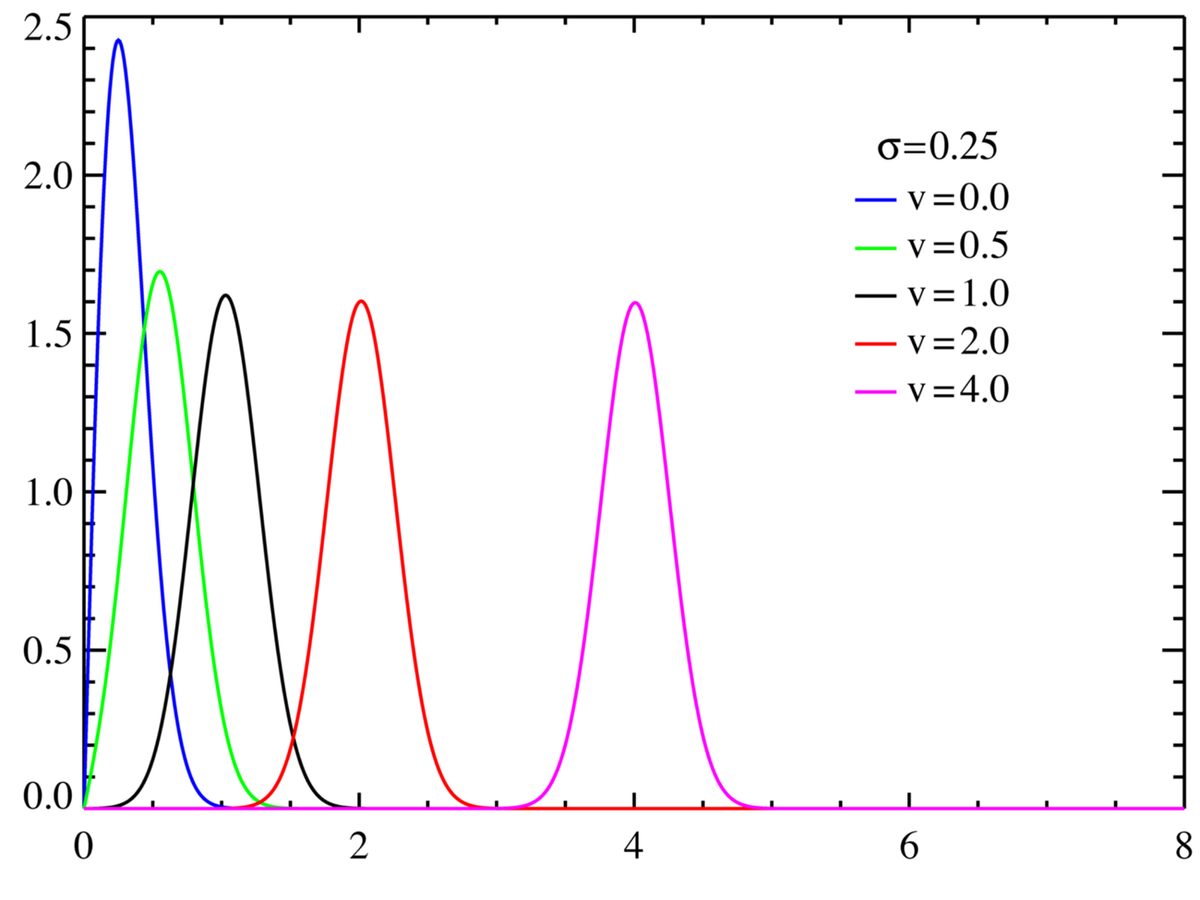
En supposant que la distribution est centrée sur un point de coordonnées (ν,ν), la densité de probabilité devient :
où I0(z) est la Fonction de Bessel modifiée de première espèce et d'ordre 0.
Distributions liées
- La variable
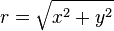
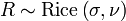
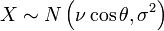
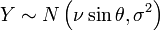
- Pour obtenir une variable
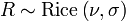
- 1. Tirer P selon une loi de Poisson, de paramètre
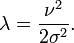
- 2. Tirer X selon une loi du Chi-deux avec 2P + 2 degrés de liberté.
- 3. Poser
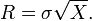
- Si
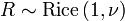
Propriétés
Moments
Les premiers moments (non-centrés) sont:
où, Lν(x) représente un Polynôme de Laguerre.
Pour le cas ν = 1/2:
Généralement les moments sont donnés par
où s = σ1/2.
Lorsque k est pair, les moments deviennent des polynômes en σ et ν.
Cas limites
Pour de grandes valeurs de l'argument, le polynôme de Laguerre devient (voir Abramowitz & Stegun §13.5.1)
On peut constater que lorsque ν devient grand ou que σ devient petit, alors la moyenne devient ν et la variance σ2.
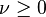
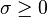
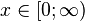
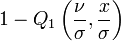
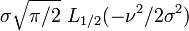
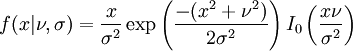
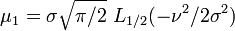
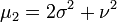
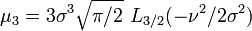
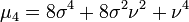
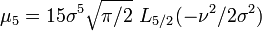
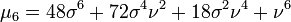
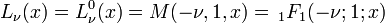
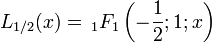
![=e^{x/2} \left[\left(1-x\right)I_0\left(\frac{-x}{2}\right) -xI_1\left(\frac{-x}{2}\right) \right].](https://static.techno-science.net/illustration/Definitions/autres/4/485fdacbcff3fdfb33e64d8e66a54da7_5ef3c57456013262f9a35bb35fec1da2.png)