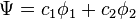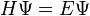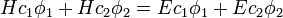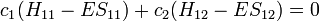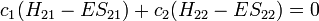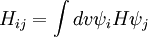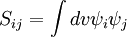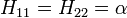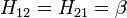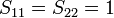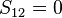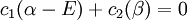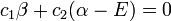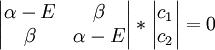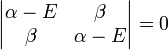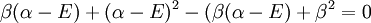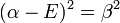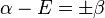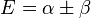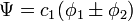Méthode de Hückel - Définition

Exemple de l'éthène

Dans le traitement selon Hückel de l'éthylène, l'orbitale moléculaire est une combinaison linéaire des orbitales atomiques 2p des atomes de carbone avec les coefficients :

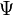
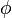
Cette équation est alors introduite dans l'équation de Schrödinger :

où est le hamiltonien et l'énergie correspondant à l'orbitale moléculaire.

L'équation est alors multipliée par (puis par ) et intégrée afin de donner l'ensemble d'équations :

où :

Les hamiltoniens entièrement diagonaux sont appelés intégrales de Coulomb et ceux de type où les atomes i et j sont liés des intégrales de résonance avec les relations suivantes :

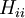
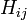
Un autre des postulats sont que l'intégrale de recouvrement entre deux orbitales atomiques est nulle :

Ceci conduit à deux équations homogènes :

avec un total de cinq variables. Après avoir converti cet ensemble en notation matricielle:

La solution triviale fournit les deux coefficients des fonctions d'ondes c égaux à zéro, ce qui n'est pas extrêmement utile pour la résolution. L'autre solution non triviale est :

qui peut être résolue en développant son déterminant:

ou

et

Après normalisation, les coefficients sont obtenus :

La constante β dans le terme d'énergie est négatif et ainsi α + β est l'énergie la plus basse, correspondant à l'orbitale la plus haute occupée (HO) et α - β à la plus basse vacante (BV).