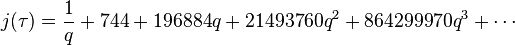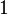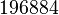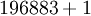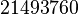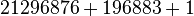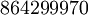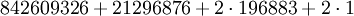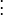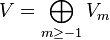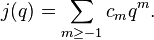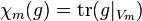Monstrous moonshine - Définition

Introduction

En mathématiques, monstrous moonshine est un terme anglais conçu par John Horton Conway et Simon P. Norton en 1979, utilisé pour décrire la connexion (alors totalement inattendue) entre le groupe Monstre M et les fonctions modulaires (particulièrement, la fonction j).

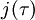
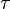
Précisément, Conway et Norton, suivant une observation initiale de John McKay, trouvèrent que le développement de Fourier de (OEIS A000521, avec désignant le ratio de demi-période) pouvait être exprimé en termes de combinaisons linéaires des dimensions des représentations irréductibles de M (OEIS A001379)

où et

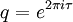
Conway et Norton formulèrent des conjectures concernant les fonctions obtenues en remplaçant les traces sur l'identité par les traces sur d'autres éléments g de M. La partie la plus saisissante de ces conjectures est que toutes ces fonctions sont de genre zéro. En d'autres termes, si est le sous-groupe de SL₂() qui fixe , alors le quotient du demi-plan supérieur du plan complexe par est une sphère avec un nombre fini de point enlevés, correspondant aux formes paraboliques de .

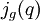
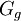
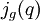
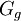
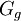
Il s'avère que derrière monstrous moonshine se trouve une certaine théorie des cordes ayant le groupe Monstre comme symétries; les conjectures faites par Conway et Norton furent démontrées par Richard Ewen Borcherds en 1992 en utilisant le théorème sans fantôme à partir de la théorie des cordes, de la théorie des algèbres vertex et des superalgèbres généralisées de Kac-Moody. Borcherds reçu la médaille Fields pour son travail, et plus de connexions entre M et la fonction j furent découvertes ultérieurement.

Versions formelles des conjectures de Conway et Norton

La première conjecture faite par Conway et Norton fut ce que l'on appela la "conjecture moonshine"; elle établit qu'il existe un M-module gradué de dimension infinie

avec pour tout m, où

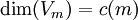
De ceci, il s'ensuit que chaque élément g de M agit sur chaque V_m et possède une valeur de caractère

qui peut être utilisée pour construire la série de McKay-Thompson de g :

.

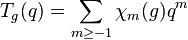
La deuxième conjecture de Conway et Norton établit ensuite qu'avec V comme ci-dessus, pour chaque élément g de M, il existe un sous-groupe de genre zéro K de , commensurable avec le groupe modulaire Γ :

, tel que est la fonction modulaire principale normalisée pour K.

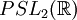
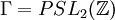
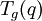
La démonstration de Borcherds

La démonstration de Richard Ewen Borcherds de la conjecture de Conway et Norton peut être séparée en cinq étapes majeures comme ce qui suit :

1. Une algèbre vertex V est construite, c’est-à-dire une algèbre graduée pouvant effectuer les représentation moonshine sur M, et il est vérifié que le module Monstre possède une structure d'algèbre vertex invariante sous l'action de M. V est ainsi appelée l'algèbre vertex Monstre.
2. Une algèbre de Lie est construite à partir de V en utilisant le théorème "sans fantôme" de Goddard-Thorn à partir de la théorie des cordes; ceci est une algèbre de Lie Kac-Moody généralisée.
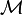
3. Un dénominateur identité pour est construit, c’est-à-dire relié aux coefficients de .
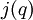
4. Un nombre de dénominateurs identités tordus sont construits qui sont reliés de manière similaire aux séries .
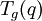
5. Les dénominateurs identités sont utilisés pour déterminer les nombres c_m, utilisant les opérateurs de Hecke, l'homologie d'algèbre de Lie et les opérations d'Adams.

Ainsi, la démonstration est complétée. Borcherds fut plus tard cité comme ayant dit "j'étais sur la Lune lorsque j'ai démontré la conjecture moonshine (clair de lune)", et "Je me demande quelquefois si c'est ce que l'on ressend lorsque l'on prend certaines drogues. Je ne le sais pas actuellement, comme je n'ai pas testé cette théorie sur moi."