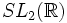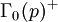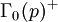Monstrous moonshine - Définition
La liste des auteurs de cet article est disponible ici.
Le module Monstre
Il fut montré plus tard par A. Oliver L. Atkin, Paul Fong et Frederic L. Smith en utilisant des calculs informatiques qu'il existe en effet une représentation graduée de dimension infinie du groupe Monstre dont les séries de McKay-Thompson sont précisément les Hauptmoduls trouvés par Conway et Norton, I. B. Frenkel, J. Lepowsky et A. Meurman construisirent explicitement cette représentation en utilisant les opérateurs vertex. Le module résultant est appelé le module Monstre.
Pourquoi « monstrous moonshine » ?
Le terme « monstrous moonshine » fut inventé par Conway, qui, lorsque John McKay lui dit à la fin des années 1970 que les coefficients de q (concrêtement 196 884) étaient précisément la dimension de l'algèbre de Griess (et ainsi exactement un de plus que le degré de la plus petite représentation fidèle complexe du groupe Monstre), répondit que ceci était « moonshine » (au sens de « dingue » ou « idées folles »). Ainsi, le terme fait référence non seulement au groupe Monstre M; il fait aussi référence à la folie perçue concernant la relation compliquée entre M et la théorie des fonctions modulaires.
Cependant, « moonshine » est aussi un mot d'argot pour un whiskey distillé illégalement, et en fait, le nom peut être expliqué à la lumière de ceci. Le groupe Monstre fut étudié dans les années 1970 par les mathématiciens Fricke, Andrew Ogg et John G. Thompson; ils étudièrent le quotient du plan hyperbolique par les sous-groupes de