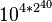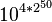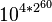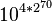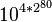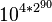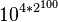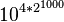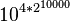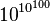Nom des grands nombres - Définition
La liste des auteurs de cet article est disponible ici.
Système d'Archimède
Un des premiers exemples connus est le décompte que fit Archimède du nombre de grains de sable que pouvait contenir l'univers, dans l'Arénaire (Ψάμμιτης). Pour cela, il généralisa le système de numération grec, dont le terme le plus élevé s'appelait la myriade (104), ce qui permettait donc aux grecs de compter jusqu'à 99 999 999 (soit 108-1, la myriade de myriade n'ayant pas de nom).
Archimède appela ces nombres nommables en grec des « nombres de premier ordre » ; et appela la myriade de myriade, soit 108, l'unité de base des « nombres de deuxième ordre ». En prenant ce nombre comme nouvelle unité, Archimèdes était capable de nommer 99 999 999 nombres « de deuxième ordre », jusqu'à 108·108=1016. Ce nombre est à son tour pris comme l'unité des « nombres de troisième ordre », et ainsi de suite.
Archimède continua sa construction logique pour tous les « ordres » qui pouvaient être nommés en grec, c’est-à-dire jusqu'au nombre d'ordre une myriade de myriade, soit
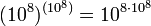
Archimède prolongea cette construction en prenant à nouveau ce nombre comme unité de base, ce qui lui permit d'étendre le système de dénomination jusqu'à
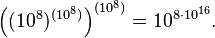
À ce point, Archimède se servit de ce système de désignation pour estimer le nombre de grains de sable que pouvait contenir l'univers, parce que « innombrable comme les grains de sable » représentait pour les grecs l'exemple archétypal de quelque chose qui ne pouvait pas être compté. Il trouva comme ordre de grandeur « mille myriades du huitième ordre » (soit 1063).
Autres systèmes de grands nombres
Système Gillion
Proposé par Russ Rowlett, basé sur les préfixes numériques grecs, et les puissances de mille :
|
|
|
Système Myriade
Proposé par Donald E. Knuth, ce système est une autre manière de généraliser les myriades grecques: au lieu que chaque « ordre de grandeur » corresponde à un regroupement de quatre chiffres, comme pour Archimède, Knuth considère que chaque ordre de grandeur peut avoir deux fois plus de chiffres que le précédent.
Au delà des noms où l'on reconnaît la présence du « y » caractéristique, il utilise des séparateurs différents pour des groupes de 4, 8, 16, 32 ou 64 chiffres (respectivement la virgule, le point-virgule, et les deux points, l'espace et l'apostrophe ; le séparateur décimal reste le point dans cette notation). Ils sont formés sur des puissances de deux successives des puissances de dix mille (myriade). Ce système permet d'écrire et nommer des nombres énormes (le premier grand nombre qui ne peut être exprimé avec les dénominations classiques est l'oktyllion, la mille-vingt-quatrième puissance de la myriade). Toutefois, le nom « myriade » reste le plus connu car il correspond à une dénomination historique.
Toutefois les noms sont rarement utilisés car ils sont souvent homonymes et homophones d’autres nombres (y compris en anglais où ces noms ont été définis), et créent de nouvelles ambiguïtés avec les échelles courtes et longues.
| Valeur | Nom | Notation |
|---|---|---|
| 100 | Un | 1 |
| 101 | Dix | 10 |
| 102 | Cent | 100 |
| 103 | Mille | 1000 |
| 104 | Myriade | 1,0000 |
| 105 | Dix myriades | 10,0000 |
| 106 | Cent myriades | 100,0000 |
| 107 | Mille myriades | 1000,0000 |
| 108 | Myllion | 1;0000,0000 |
| 1012 | Myriade de myllions | 1,0000;0000,0000 |
| 1016 | Byllion | 1:0000,0000;0000,0000 |
| 1024 | Myllion de byllions | 1;0000,0000:0000,0000;0000,0000 |
| 1032 | Tryllion | 1 0000,0000;0000,0000:0000,0000;0000,0000 |
| 1064 | Quadryllion | 1'0000,0000;0000,0000:0000,0000;0000,0000 0000,0000;0000,0000:0000,0000;0000,0000 |
| 10128 | Quintyllion | |
| 10256 | Sextyllion | |
| 10512 | Septyllion | |
| 101024 | Octyllion | |
| 102048 | Nonyllion | |
| 104096 | Decyllion | |
| 108192 | Undecyllion | |
| 1016,384 | Duodecyllion | |
| 1032,768 | Tredecyllion | |
| 1065,536 | Quattuordecyllion | |
| 10131,072 | Quindecyllion | |
| 10262,144 | Sexdecyllion | |
| 10524,288 | Septendecyllion | |
| 101,048,576 | Octodecyllion | |
| 102,097,152 | Novemdecyllion | |
| 104,194,304 | Vigintyllion | |
| 104,294,967,296 | Trigintyllion | |
|
| Quadragintyllion | |
|
| Quinquagintyllion | |
|
| Sexagintyllion | |
|
| Septuagintyllion | |
|
| Octogintyllion | |
|
| Nonagintyllion | |
|
| Centyllion | |
|
| Millillion | |
|
| Myryllion |
Le système Googol
Les termes googol et googolplex furent inventés par Milton Sirotta, neveu du mathématicien Edward Kasner, qui les introduisit dans une publication de 1940, Mathematics and the Imagination, où il décrit cette invention :
Le terme « googol » a été inventé par un enfant, le neveu du Dr Kasner, alors âgé de huit ans. On lui avait demandé d'imaginer un nom pour un nombre très grand, par exemple un 1 suivi d'une centaine de zéros. Il était sûr que ce nombre n'était pas infini, et tout aussi certain qu'il n'avait pas de nom propre. Il suggéra le terme « googol », et dans la foulée en proposa un autre pour un nombre encore plus grand: le « googolplex ». Un googolplex est beaucoup plus grand qu'un googol, mais reste fini, ce que l'inventeur du terme fit rapidement remarquer. Au départ, la définition proposée était un 1, suivi d'autant de zéro qu'on pourrait en écrire sans tomber de fatigue. C'est certainement ce qui risquerait d'arriver si quelqu'un essaye d'écrire un googolplex, mais deux personnes différentes seraient fatiguées au bout d'un temps différent, et ça n'aurait pas de sens que Carnera soit un meilleur mathématicien que Einstein simplement parce qu'il a une meilleure endurance. Pour cette raison, le googolplex est un nombre spécifique, mais avec tellement de zéros derrière son « un » que le nombre de zéros est lui-même d'un googol.
Par la suite, Conway et Guy ont suggéré comme extension que un N-plex corresponde par convention à 10N. Avec ce système, un googol-plex vaut bien 10googol, et un googolplexplex vaut 10googolplex.
D'autres auteurs ont proposé les formes googolduplex, googoltriplex, etc., pour désigner respectivement 10googolplex, 10googolduplex, et ainsi de suite.
| 10100 | Googol |
|
| Googolplex |
| 10-N | N-minex |
| 10N | N-plex |