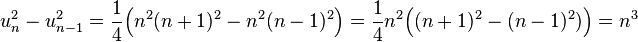Nombre triangulaire - Définition
La liste des auteurs de cet article est disponible ici.
Autres propriétés
Généralisations
Si, au lieu de calculer la somme des n premiers nombres entiers strictement positifs, on calcule les n premiers carrés strictement positifs que l'on appelle cn, on obtient la formule suivante :
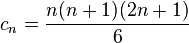
L'intuition de l'exactitude de cette formule est donnée par la preuve sans mots suivante :
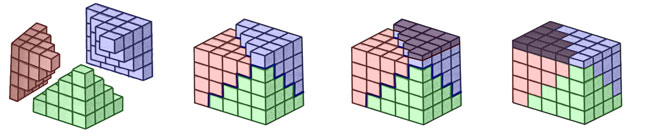
Ce résultat se généralise pour la somme des n premières puissances strictement positives. Cette somme porte le nom de formule de Faulhaber. Il est aussi possible de généraliser en considérant le nombre de points sn,d contenus dans un simplexe dont les cotés sont de longueurs n, dans un espace de dimension d. On obtient :
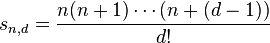
Entier somme de trois nombres triangulaires
A condition de considérer zéro comme un nombre triangulaire, Pierre de Fermat conjectura que tout entier est somme de trois nombres triangulaires. La preuve de l'exactitude de cette conjecture fût apportée à la fin du XVIIIe siècle par Gauss.
La démonstration ici n'est pas géométrique. L'arithmétique telle qu'on la concevait à l'époque de Pythagore est impuissante pour prouver des résultats de cette nature. La partie difficile de la preuve est le théorème des trois carrés, qui a pour conséquence que tout entier positif congru à 3 modulo 8 est somme de trois carrés parfaits. Soit M un nombre entier positif, 8M + 3 est somme de trois carrés. De plus chaque carré de la somme est impair, sinon leur somme ne serait pas congru à 3 modulo 4. On en déduit l'existence de trois entiers x, y et z tels que :
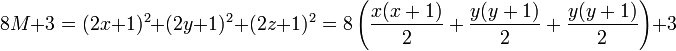
Cette dernière égalité implique le résultat recherché, M est la somme des trois nombres triangulaires d'indice x, y et z.
Résultats géométriques
Les grecs de l'école de Pythagore n'avaient pas connaissance des théorèmes fondamentaux de l'arithmétique élémentaire, comme le lemme d'Euclide, le théorème de Bachet-Bézout ou encore le théorème fondamental de l'arithmétique. Ils ont développé une arithmétique différente et les résultats présentés ici sont un peu à l'image de leur conception de l'arithmétique. Néanmoins, comme il n'existe pas de texte directement écrit sur cette question par les membres de cette école, il est difficile de relier des résultats précis à des dates ou des noms de membres de l'école, ainsi que d'être catégorique sur le fait qu'un résultat était bien connu d'eux.
Somme de deux nombres triangulaires consécutifs

La figure de droite montre que la somme du quatrième et du cinquième nombre triangulaire forme le cinquième carré parfait, c'est à dire 25. Ce résultat n'est pas uniquement vrai pour la valeur cinq :
Proposition — Soit n un nombre entier strictement positif. La somme des deux nombres triangulaires d'indice n et n + 1 est égale à (n + 1) x (n + 1), c'est à dire au carré de n + 1.
La formule précédente permet d'établir ce résultat :
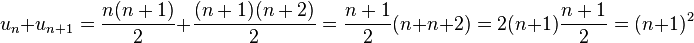
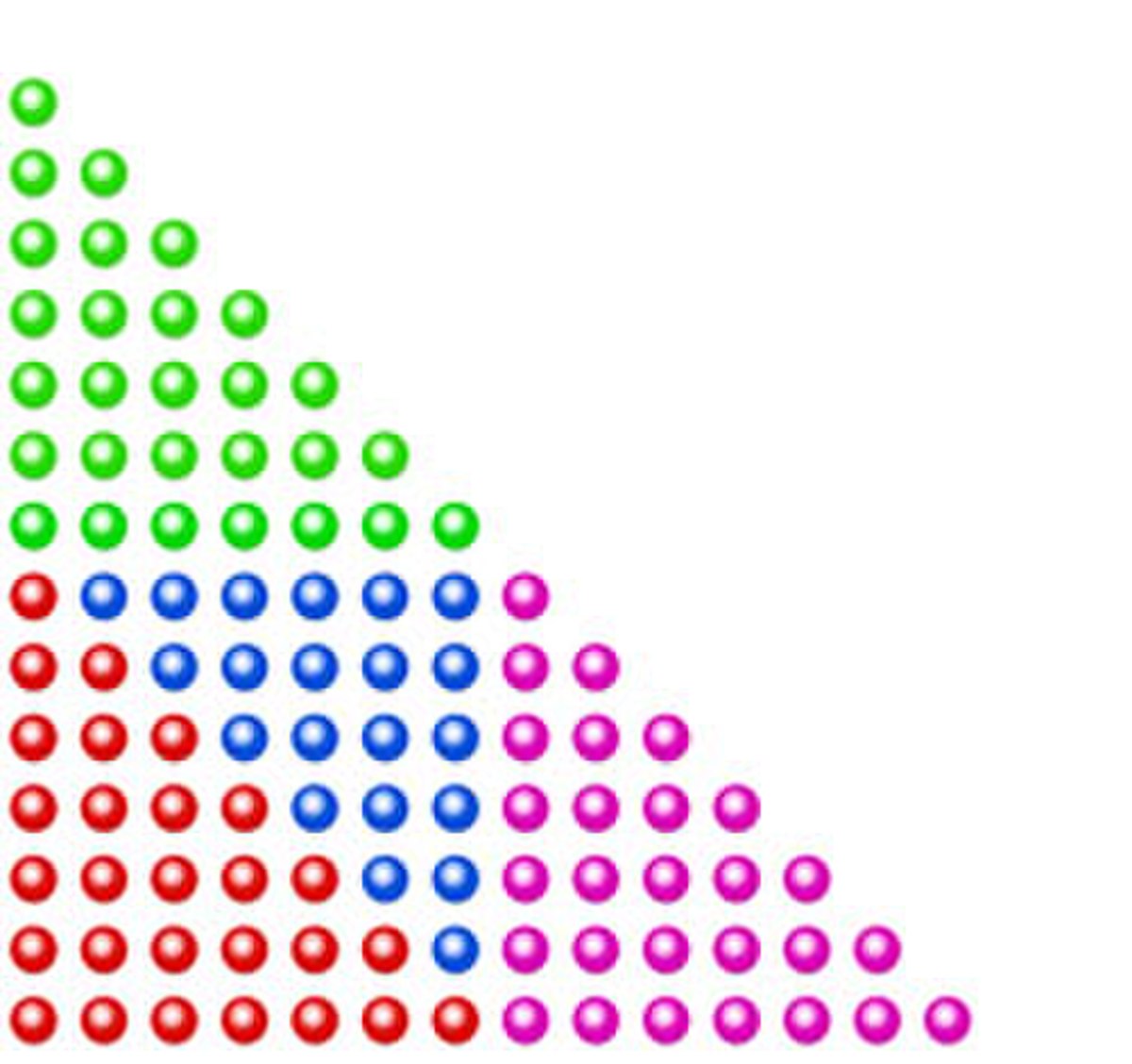
Un nombre triangulaire est somme de quatre nombres triangulaires
Les deux graphiques du paragraphe indiquent que le nombre triangulaire d'indice n est somme de quatre nombres triangulaires. Ceci est vrai quelle que soit la parité de l'indice n. En effet, u14 est la somme de trois fois u7 et de u6 et u15 est la somme trois fois u7 et de u8. Cette proposition s'exprime de la manière suivante :
Proposition — Soit n entier strictement positif, u2n et u2n + 1 sont somme de quatre nombres triangulaires et vérifient les formules :
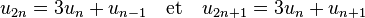
En effet :
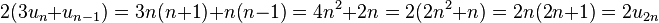
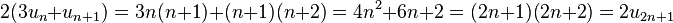
Un carré parfait avec un unique nombre triangulaire
La figure de droite montre qu'il est possible d'emboiter huit nombres triangulaires d'indice 7 pour former un carré de coté 15, auquel il manque la pastille centrale, en gris sur la figure. Une fois encore, ce résultat se généralise :
Proposition — Soit n entier strictement positif, le carré parfait (2n + 1)2 est égal à la somme de huit fois un et de l'unité :
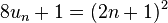
En effet, ce résultat est directement l'application d'une identité remarquable :
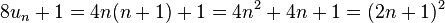
Cube et nombre triangulaire
Un autre résultat traite des cubes. Il s'énonce ainsi :
Proposition — Si n est un entier supérieur à deux, la différence entre les carrés du nombre triangulaire d'indice n et n - 1 est égale au cube de n.
Il est découvert par le mathématicien arabe Al-Karaji, qui l'exprime d'une manière presque équivalente :
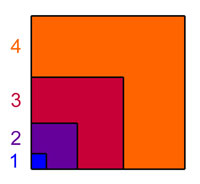
Proposition — Si n est un entier strictement positif, la somme des n premiers cubes positifs est égal au carré du nombre triangulaire d'indice n.
L'illustration géométrique à droite permet de se convaincre de la véracité de ses propositions. L'aire de la zone orange de la figure est appelée nombre gnomonique. Elle est constituée de deux rectangles de base 4 et de côté le nombre triangulaire d'indice 4, c'est à dire 10. Ces deux rectangles se recoupent sur un carré de côté 4, on en déduit que l'aire orange est égale à 5 x 4 x 4 - 4 x 4, ou encore 43. Ce raisonnement est valable sur chaque nombre gnomonique, l'aire du carré de côté le nombre triangulaire d'indice 4 est égal la somme des 4 premiers cubes. De cette démonstration d'Al-Karaji, on déduit la première proposition.
On peut aussi raisonner algébriquement à partir de la première proposition :