Moment magnétique - Définition

Introduction

En physique, le moment magnétique est une grandeur vectorielle qui permet de mesurer l'intensité d'une source magnétique. La source peut être une distribution de courant, ou bien un matériau présentant un moment magnétique spontané. Ce moment magnétique est souvent noté m, ou bien μ.

Un dipôle magnétique, caractérisé par son moment magnétique, est analogue à un aimant droit.

Définition

Pour une distribution de courant j, on définit le moment magnétique m par la formule

.

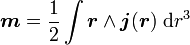
Pour un système constitué de boucles de courant fermées, m est indépendant du choix de l'origine, à l'instar du dipôle électrostatique dont la définition est indépendante de l'origine quand la somme des charges électriques le composant est nulle. L'unité du moment magnétique dans le système international d'unités est l'ampère-mètre carré (A·m²).

Le modèle le plus simple de moment magnétique est celui d'une boucle de courant (courant électrique circulant dans un élément de bobine par exemple). Un champ magnétique appliqué à cette boucle tendra à faire tourner la boucle de manière à ce qu'elle soit perpendiculaire au champ magnétique, le courant tournant dans le sens direct par rapport au plan orienté par le champ magnétique. Par exemple, une bobine électrique parcourue par un courant et libre de ses mouvements s'alignera sur l'aimant qu'on approche d'elle. Le moment magnétique multiplié par le champ donne le couple de force qui s'applique.

Le moment magnétique dans la matière

Les propriétés magnétiques de la matière s'expliquent par la présence de courants microscopiques dans la matière, liés au mouvement des électrons autour du noyau, aux répartitions des nuages électroniques dans les molécules et structures cristallines, et au moment magnétique de spin propre (spin) d'un électron.

Le moment magnétique d'une boucle de courant entourant une surface est μ = i S où S est un vecteur orthogonal à la surface sous tendue par le courant électrique i et d'amplitude égale à son aire (orienté selon la normale d'Ampère selon le sens de rotation du courant).

Un moment magnétique est induit s'il est créé par la présence de B. D'après la loi de Lenz, un moment magnétique induit s'oppose au champ B qui l'a créé.

Certains atomes (ou molécules) portent des moments magnétiques même si B = 0, on dit qu'ils portent un moment magnétique permanent. Ce phénomène est à l'origine des propriétés ferromagnétique de certains matériaux.

Lien avec le champ magnétique

Champ magnétique créé

Loin d'une distribution de courant, le champ magnétique B(r) généré par un moment magnétique situé en r' décroît comme l'inverse du carré de la distance. Sa valeur précise s'écrit

.

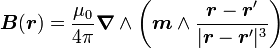
Cette formule peut se développer pour donner

.

Lien avec le moment cinétique

En mécanique classique, on peut montrer le lien existant entre le moment cinétique orbital L et le moment magnétique μ d'une configuration possédant des charges en mouvement.

On considère une particule (un électron) de masse m suivant une trajectoire circulaire de rayon r à une vitesse v. Le moment cinétique vaut alors

.

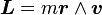
Le moment magnétique associé à ce courant, autrement dit au déplacement de l'électron qui génère un courant électrique i, est:

,

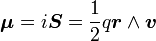
où q est la charge de la particule et S la surface délimitant l'extension de son déplacement.

En combinant les deux relations ci-dessus, on obtient ainsi la relation suivante entre moments cinétique et magnétique :

,

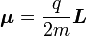
ou bien

,

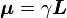
où γ est appelé rapport gyromagnétique du dipôle considéré.

Dipôle magnétique dans un champ magnétique

En présence d'un champ magnétique, le fer s'aimante à son tour et devient un dipôle. Il est alors soumis aux forces créées par un aimant droit et s'oriente selon les lignes de champ.

A chaque dipôle magnétique est associé un moment magnétique μ. En présence d'un champ magnétique B, ce dipôle va être soumis à un couple C et une force F, auxquels on peut associer une énergie potentielle E. Ces dernières sont définies par les relations suivantes :

,

,

.

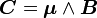
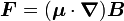
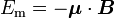
L'équation relative au couple indique que la dérivée temporelle du moment cinétique d'un dipôle magnétique est égal au couple C. Or celui-ci fait intervenir le produit vectoriel du moment magnétique avec le champ magnétique. Mais comme moment magnétique et moment cinétique sont proportionnel, l'équation indique que la dérivée du moment cinétique est proportionnelle au produit vectoriel du moment cinétique lui-même avec le champ. Ainsi, en présence d'un champ magnétique, un dipôle magnétique va-t-il être l'objet d'un phénomène de précession appelé dans ce contexte précession de Larmor.