Paramètres de Milankovi? - Définition
La liste des auteurs de cet article est disponible ici.
Introduction
Les paramètres de Milanković ou cycles de Milanković correspondent à trois phénomènes astronomiques affectant certaines planètes au moins du système solaire : l'excentricité, l'obliquité et la précession. La terminologie de « paramètres de Milankovitch » est surtout utilisée dans le cadre de la théorie astronomique des paléoclimats.
Joseph-Alphonse Adhémar, James Croll et Milutin Milanković sont les principaux scientifiques ayant avancé l'idée que ces trois paramètres interviennent dans les variations climatiques naturelles, en particulier sur Terre. Cette hypothèse n'a été soutenue par des données expérimentales cohérentes qu'en 1976, avec l'article fondamental de Hays, Imbrie et Shackleton.
Ces changements climatiques naturels ont pour principale conséquence les périodes glaciaires et interglaciaires. Leur étude en termes de phénomènes périodiques est du ressort la cyclostratigraphie.
Les paramètres sur Terre
Nous considérons tout d'abord que le Soleil ne se déplace pas (nous n'avons pas à prendre en compte le déplacement du Soleil dans l'espace).
L'excentricité de l'orbite terrestre
La Terre décrit dans l'espace une ellipse dont le Soleil occupe l'un des foyers, mais cette ellipse se déforme (jusqu'à une excentricité maximum de 0,06) et se déplace dans l'espace (comme si elle oscillait de gauche à droite). En effet, au cours du temps, la distance Terre/Soleil varie entre 129 000 000 et 187 100 000 km. Actuellement, la distance Terre/Soleil admise est de 149 597 870,691 km, soit un aplatissement de 1,67%.
Cette excentricité est due aux attractions gravitationnelles exercées entre la Terre et les autres planètes du système solaire ainsi que le Soleil. Chaque planète attirant la Terre selon les lois de Newton, et les forces qu'elles lui appliquent n'étant pas les mêmes, l'excentricité de l'orbite terrestre peut varier d'un facteur 10 (en gros de 0.005 à 0.06). Le phénomène se présente comme somme de solutions périodiques (20 termes pour La2004) dont voici les cinq premiers :
e(t) = 0,027 557 9 + 0,010 739 cos(3,199 279 kt + 170,739 b) + 0,008 147 cos(13,651 920 kt + 109,891 b) + 0,006 222 cos(10,456 224 kt - 60,044 b) +0,005 287 cos(13,109 803 kt - 86,140 b) +0,004 492 cos(9,909 679 kt + 100,224 b).
[Ici, k = 2π/1 296 000 et b = π/180]. La figure est présentée ci-dessous.
L'obliquité terrestre
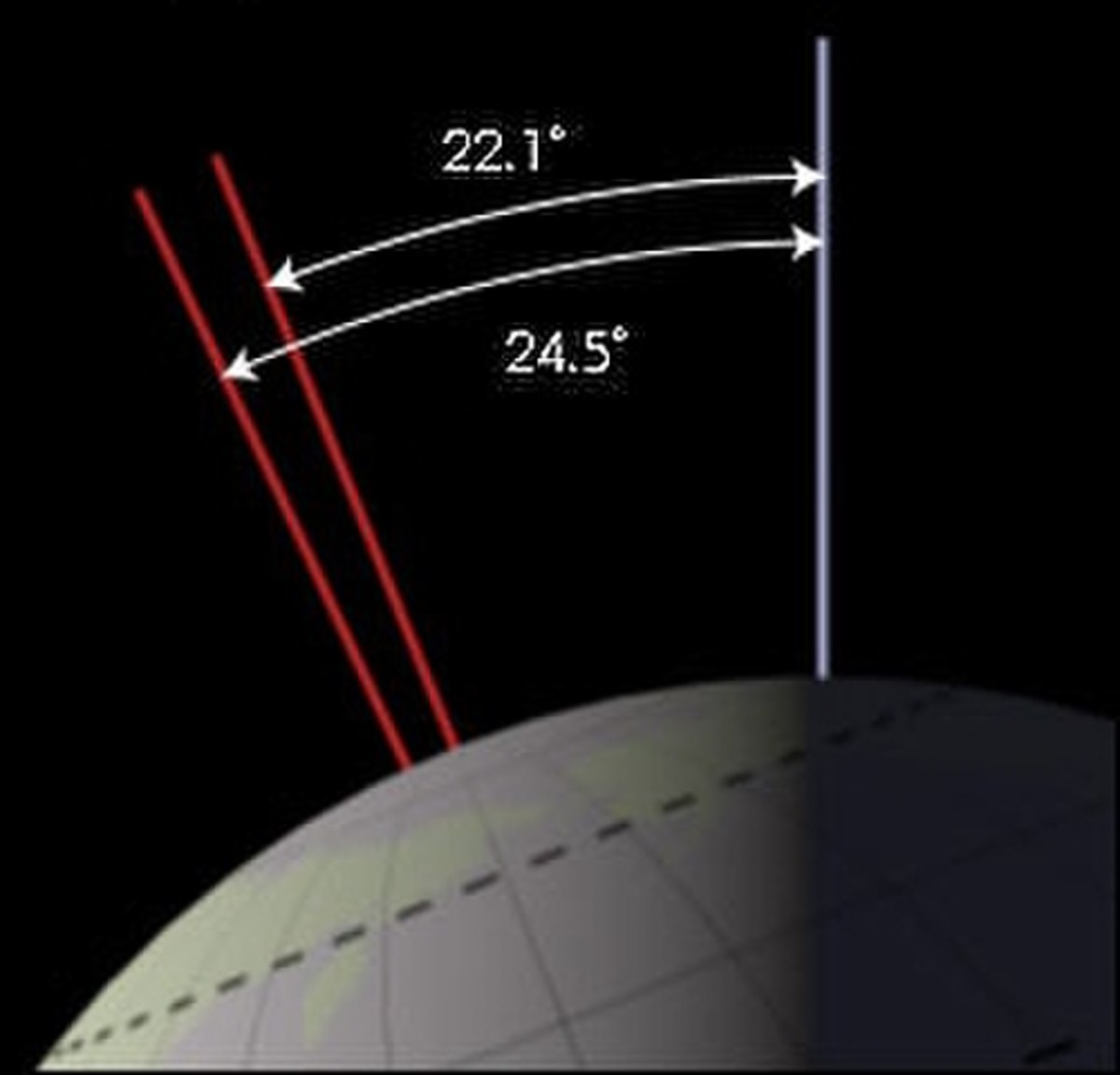
L'inclinaison terrestre varie entre 21,8° et 24,4°. Actuellement, elle est de 23°26,5'. Cette obliquité est due elle aussi aux interactions gravitationnelles que la Terre subit de la part des planètes.
La périodicité de ce phénomène est essentiellement de 41 000 ans.
Cette variation est faible : par comparaison, l'obliquité martienne varie entre 14,9° et 35,5°. En fait, c'est la présence de la lune qui agit sur le bourrelet équatorial de la terre et lui donne la rapide précession d'Hipparque de 26000 ans, et de ce fait, la Lune place la Terre pour son obliquité actuelle dans une zone de faible perturbation (Laskar & Robutel(1993)).
Néanmoins, les faibles variations de cette obliquité ont de larges conséquences sur l'insolation à la latitude de 65°, que l'on considère comme le critère le plus fiable de fonte des inlandsis.
La précession terrestre
La Terre ne tourne pas sur elle-même comme un ballon parfaitement sphérique mais plutôt comme une toupie car elle est soumise à la précession. Cette précession provient du fait que les attractions du Soleil et de la Lune ne sont pas uniformes sur Terre à cause du bourrelet équatorial de la Terre. Ceci a deux conséquences différentes.
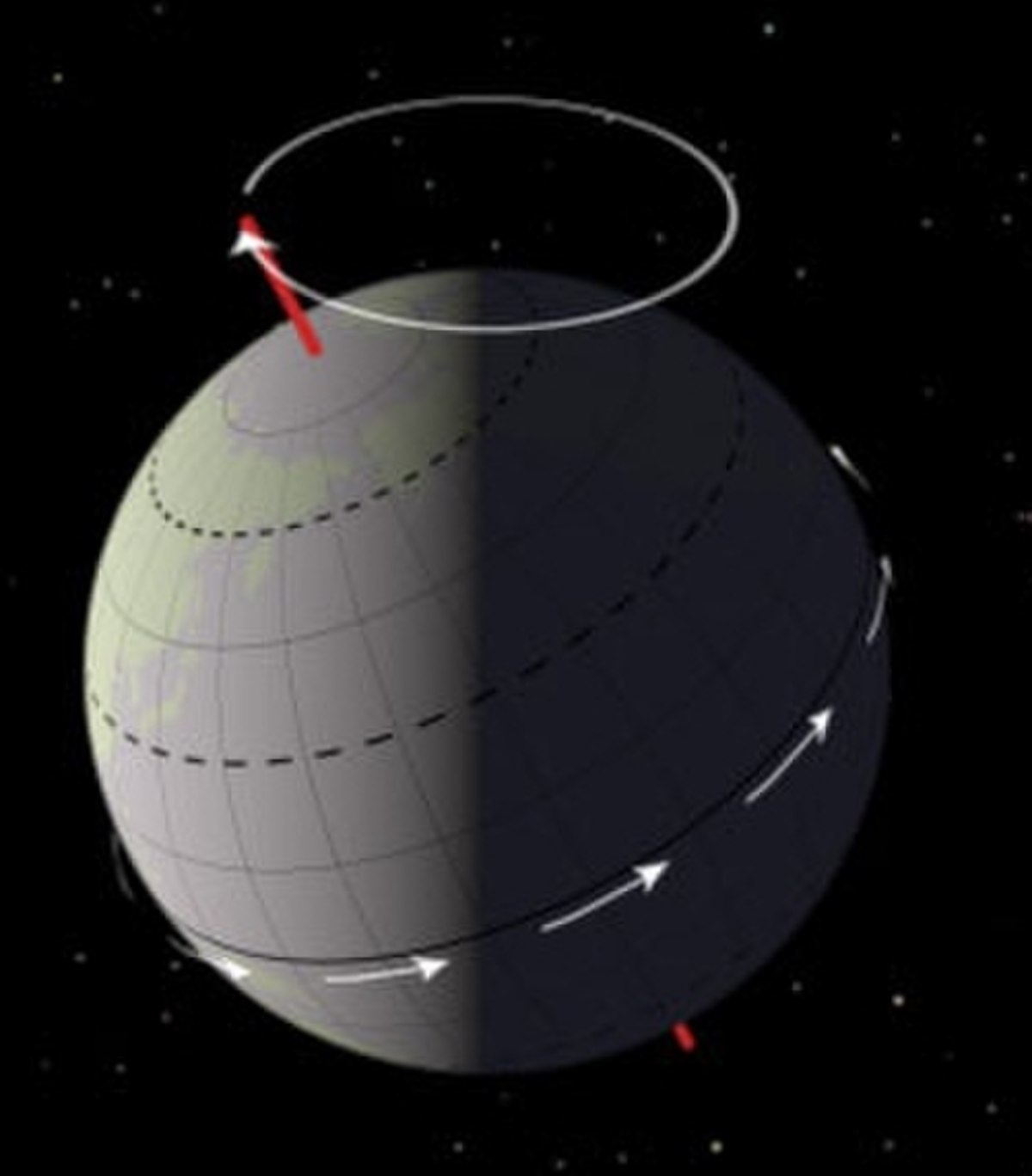
D'un côté, cela va influer sur l'indication du Pôle Nord céleste (quelle étoile nous indique le nord). Reprenons pour cela notre toupie :
- La toupie tourne dans un premier temps droite puis en perdant sa vitesse, sa tige va commencer à dessiner une sorte de cercle.
Cette tige sur Terre est en réalité l'axe nord-sud (passant par les deux pôles géographiques), cet axe dessine dans l'espace un cercle par rapport au pôle Nord céleste (qui ne varie pas). L'axe nord-sud effectue le cercle complet en 25 760 ans. Aujourd'hui, α Ursae Minoris, appelée étoile polaire, se situe à 0,8° du pôle Nord céleste.
D'un autre côté, cela influe sur ce que l'on appelle la précession des équinoxes (ce qui détermine les « changements de saisons » astronomiquement parlant).
Le point vernal rétrograde (se déplace vers l'ouest) de 50,38″ par an, mais la précession due aux autres planètes du système solaire (donc hors Soleil et Lune) est de 0,12″ dans le sens inverse ; donc la précession se fait de 50,26″ par an vers l'ouest.
La nutation
Nous avons dit plus haut que la rotation terrestre sur elle même était responsable de la précession terrestre qui se remarque par un cercle (fictif dans l'espace). En fait, dire que ce cercle est parfait, c'est oublier l'attraction de la Lune (et du Soleil mais dans un rôle mineur) et la nutation (qui est une conséquence de cette attraction). En effet, la Lune attire la Terre (nous pouvons d'ailleurs le voir avec le phénomène des marées) et cette attraction se remarque par une légère oscillation (ressemblant à une sinusoïde) du cercle de précession. Le motif de ce phénomène dure 18,6 ans.
Le phénomène résulte du fait que l'influence de la Lune n'est pas toujours identique au cours du temps : elle est minimale lorsque la distance angulaire entre la Lune et l'équateur est la plus petite, elle est maximale lorsque la distance est la plus grande. Comme ce phénomène n'est pas très influent pour le sujet, nous allons l'ignorer pour les conséquences des paramètres de Milanković.