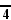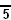Polygone de Pétrie - Définition
Source: Wikipédia sous licence CC-BY-SA 3.0.
La liste des auteurs de cet article est disponible ici.
La liste des auteurs de cet article est disponible ici.
Polygones de Pétrie des polyèdres réguliers
Il y a 5 polyèdres réguliers (voir solide de Platon). Le polygone de Pétrie d'un polyèdre régulier {p,q} (voir symbole de Schläfli) possède h côtés, où :
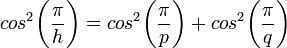
Les polyèdres duaux (voir dualité), {p,q} et {q,p}, sont donc contenus par les mêmes polygones de Pétrie.

| ||||
| tétraèdre | cube | octaèdre | dodécaèdre | icosaèdre |
|
|
|
|
|
|
| centré sur une arête | centré sur un sommet | centré sur une face | centré sur une face | centré sur un sommet |
| 4 côtés | 6 côtés | 6 côtés | 10 côtés | 10 côtés |
| V:(4,0) | V:(6,2) | V:(6,0) | V:(10,10,0) | V:(10,2) |
Les polygones de Pétrie sont les bords (en rouge) de ces projections orthogonales. Les lignes bleues représentent les arêtes de devant, et les lignes noires les arêtes de derrière.
Les sommets, qui sont sur des cercles concentriques, sont comptés par "couches" à partir de l'extérieur jusqu'à l'intérieur, par la notation du polygone de Pétrie : V:(a,b,...) avec un 0 à la fin si la couche centrale est vide.