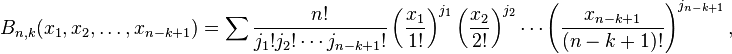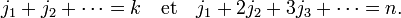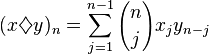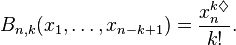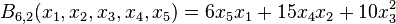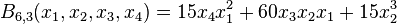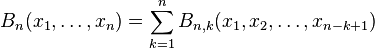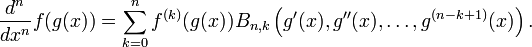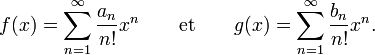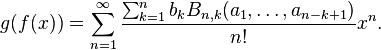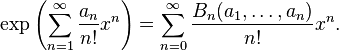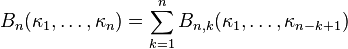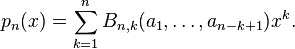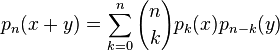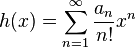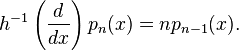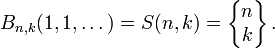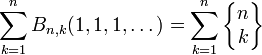Polynômes de Bell - Définition
La liste des auteurs de cet article est disponible ici.
Introduction
En mathématiques, et plus précisément en combinatoire, les polynômes de Bell, nommés ainsi d'après le mathématicien Eric Temple Bell, sont donnés par
où la somme porte sur toutes les suites j1, j2, j3, ..., jn−k+1 d'entiers tels que
Identité de convolution
Pour des suites xn, yn, n = 1, 2, ..., on peut définir un produit de convolution par
(les bornes de sommation étant 1 et n − 1, et non 0 et n).
Soit
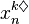
Alors
Interprétation combinatoire
Si l'entier n est partitionné en une somme dans laquelle "1" apparait j1 fois, "2" apparait j2 fois, et ainsi de suite, alors le nombre de partitions d'un ensemble à n éléments qui correspondent à cette partition de l'entier n quand on ne distingue plus les éléments de l'ensemble est le coefficient correspondant du polynôme.
Exemples
Par exemple, nous avons
car il y a
- 6 partitions d'un ensemble à 6 éléments de la forme 5 + 1,
- 15 partitions de la forme 4 + 2, et
- 10 partitions de la forme 3 + 3.
De même,
car il y a
- 15 partitions d'un ensemble à 6 éléments de la forme 4 + 1 + 1,
- 60 partitions de la forme 3 + 2 + 1, et
- 15 partitions de la forme 2 + 2 + 2.
Polynômes de Bell complets
La somme
est parfois appelée n-ème polynôme de Bell complet, et alors les polynômes Bn, k définis ci-dessus sont appelés des polynômes de Bell "partiels". Les polynômes de Bell complets satisfont l'identité suivante :
Applications
Formule de Faà di Bruno
La formule de Faà di Bruno peut être énoncée à l'aide des polynômes de Bell de la manière suivante :
De même, on peut donner une version de cette formule concernant les séries formelles : supposons que
Alors
Les polynômes de Bell "complets" apparaissent dans l'exponentielle d'une série formelle :
Moments et cumulants
La somme
est le n-ème moment d'une distribution de probabilité dont les n premiers cumulants sont κ1, ..., κn. Autrement dit, le n-ème moment est le n-ème polynôme de Bell complet évalué en les n premiers cumulants.
Représentations de suites polynomiales
Pour toute suite a1, a2, a3, ... de scalaires, soit
Cette suite de polynômes est de type binomial, c'est-à-dire qu'elle satisfait l'identité binomiale
pour n ≥ 0. En fait, on a le résultat réciproque suivant :
- Théorème : Toutes les suites de polynômes de type binomial sont de cette forme.
Si nous posons
en considérant cette série comme une série formelle, alors pour tout n,
Nombres de Stirling et nombres de Bell
La valeur du polynôme de Bell Bn,k(x1,x2,...)lorsque tous les xs valent 1 est un nombre de Stirling de deuxième espèce :
La somme
est le n-ème nombre de Bell, c'est-à-dire le nombre de partitions d'un ensemble à n éléments.