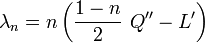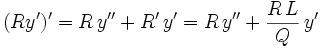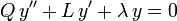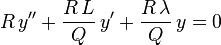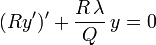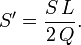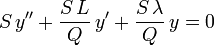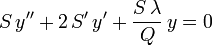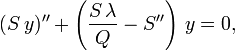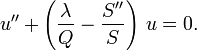Polynômes orthogonaux - Définition
La liste des auteurs de cet article est disponible ici.
Exemple : les polynômes de Legendre
Les polynômes orthogonaux les plus simples sont les polynômes de Legendre pour lesquels l'intervalle d'orthogonalité est ]-1, 1[ et la fonction poids est simplement la fonction constante de valeur 1 :
Ils sont tous orthogonaux sur ]-1, 1[ :
Tableau des polynômes orthogonaux classiques
| Nom et symbole conventionnel | Tchebychev,
| Tchebychev (seconde sorte), | Legendre,
| Hermite (forme physique),
|
|---|---|---|---|---|
| Limite d'orthogonalité |
|
|
|
|
| Poids,
|
|
|
|
|
| Normalisation |
|
|
| Coefficient dominant =
|
| Carré de la norme
|
|
|
|
|
| Coefficient dominant
|
|
|
|
|
| Coefficient suivant
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| Constante dans l'équation différentielle,
|
|
|
|
|
| Constante dans la formule de Rodrigues,
|
|
|
|
|
| Relation de récurrence,
|
|
|
|
|
| Relation de récurrence,
|
|
|
|
|
| Relation de récurrence,
|
|
|
|
|
| Nom et symbole | Laguerre associé,
| Laguerre,
|
|---|---|---|
| Limites d'orthogonalité |
|
|
| Poids,
|
|
|
| Normalisation | Coefficient dominant =
| Coefficient dominant =
|
| Carré de la norme
|
|
|
| Coefficient dominant
|
|
|
| Coefficient suivant
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| Constante dans l'équation différentielle,
|
|
|
| Constante dans la relation de Rodrigues,
|
|
|
| Relation de récurrence,
|
|
|
| Relation de récurrence,
|
|
|
| Relation de récurrence,
|
|
|
| Nom et symbole | Gegenbauer,
| Jacobi,
|
|---|---|---|
| Limites d'orthogonalité |
|
|
| Poids,
|
|
|
| Normalisation |
|
|
| Carré de la norme,
|
|
|
| Coefficient dominant
|
|
|
| Coefficient suivant
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| Constante dans l'équation différentielle,
|
|
|
| Constante dans l'équation de Rodrigues,
|
|
|
| Relation de récurrence,
|
|
|
| Relation de récurrence,
|
|
|
| Relation de récurrence,
|
|
|
Équations différentielles conduisant à des polynômes orthogonaux
Une importante classe des polynômes orthogonaux provient d'une équation différentielle de Sturm-Liouville de la forme
où Q est un polynôme quadratique donné et L un polynôme linéaire donné. La fonction f est inconnue, et la constante λ est un paramètre. On peut remarquer qu'une solution polynomiale est a priori envisageable pour une telle équation, les degrés des termes étant compatibles. Cependant, les solutions de cette équation différentielle ont des singularités, à moins que λ ne prenne des valeurs spécifiques. La suite de ces valeurs
- Q est vraiment quadratique, L est linéaire, Q a deux racines réelles distinctes, la racine de L est située entre les deux racines de Q, et les termes de plus haut degré de Q et L ont le même signe.
- Q n'est pas quadratique, mais linéaire, L est linéaire, les racines de Q et L sont différentes, et les termes de plus haut degré de Q et L ont le même signe si la racine de L est plus petite que celle de Q, ou inversement.
- Q est un polynôme constant non nul, L est linéaire, et le terme de plus haut degré de L est de signe opposé à celui de Q.
Ces trois cas conduisent respectivement aux polynômes de Jacobi, de Laguerre et d'Hermite. Pour chacun de ces cas :
- La solution est une suite de polynômes
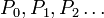
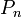
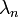
- L'intervalle d'orthogonalité est limité par les racines de Q.
- La racine de L est à l'intérieur de l'intervalle d'orthogonalité.
- En notant
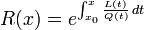
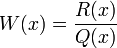
- W(x) ne peut pas s'annuler ou prendre une valeur infinie dans l'intervalle, bien qu'il puisse le faire aux extrémités.
- W(x) peut être choisi positif sur l'intervalle (multiplier l'équation différentielle par -1 si nécessaire)
En raison de la constante d'intégration, la quantité R(x) est définie à une constante multiplicative près. Le tableau ci-dessous donne les valeurs "officielles" de R(x) et W(x).
Formule de Rodrigues
Avec les hypothèses de la section précédente, Pn(x) est proportionnel à
![\frac{1}{W(x)} \ \frac{d^n}{dx^n}\left(W(x)[Q(x)]^n\right)](https://static.techno-science.net/illustration/Definitions/autres/3/3918d0b9536540fbeecf695a34d5b28f_e48ef59fff5e40051de81f965b867cc5.png)
équation mieux connue sous le nom de « formule de Rodrigues ». Elle est souvent écrite :
où les nombres en dépendent de la normalisation. Les valeurs de en sont données dans le tableau plus bas.
Pour démontrer cette formule on vérifie, dans chacun des trois cas ci-dessus, que le Pn qu'elle fournit est bien un polynôme de degré n, puis, par intégrations par parties répétées, que pour tout polynôme P,
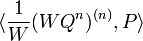
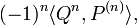
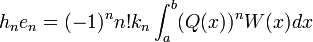
Les nombres λn
Avec les hypothèses de la section précédente,
(on remarquera que Q étant quadratique et L linéaire, Q'' et L' sont bien des constantes.)
Seconde forme de l'équation différentielle
Avec

Alors
En multipliant maintenant l'équation différentielle
par R/Q, on obtient
ou encore
C'est la forme normalisée de Sturm-Liouville de l'équation.
Troisième forme de l'équation différentielle
En posant
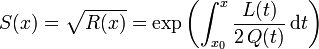
Alors :
En multipliant maintenant l'équation différentielle
par S/Q, on obtient :
ou encore
Mais
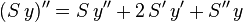
ou, en posant u = Sy,
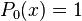
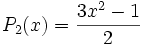
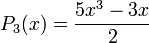
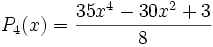
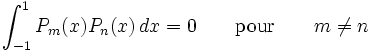
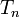
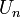
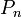
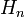
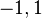
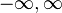
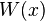
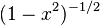
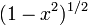
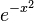
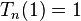
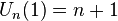
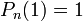
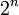
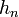
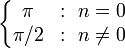
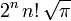
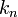
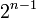
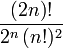
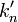
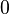
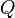
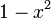
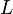
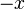
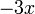
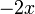
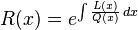
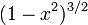
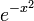
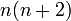
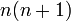
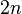
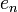
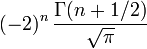
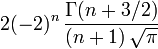
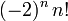
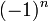
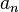
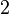
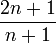
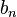
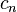
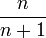
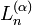
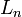
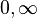
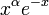
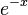
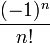
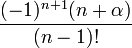
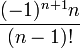

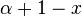
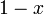
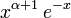
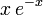
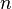
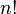
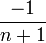
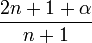
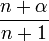
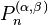
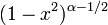
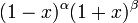
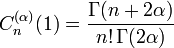
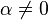
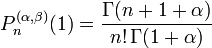
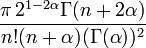
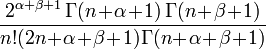
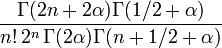
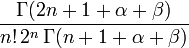
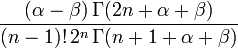
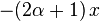
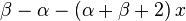
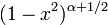
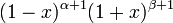
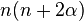
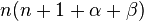
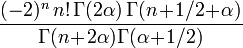
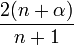
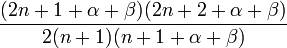
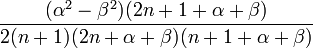
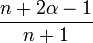
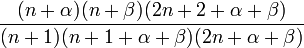
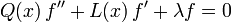
![P_n(x) = \frac{1}{{e_n}W(x)} \ \frac{d^n}{dx^n}\left(W(x)[Q(x)]^n\right)](https://static.techno-science.net/illustration/Definitions/autres/0/053c6bdce2a23cedd8699f20a10268e3_8dbad85b386d6594c099c5fdc09f5d7f.png)