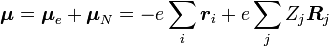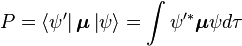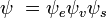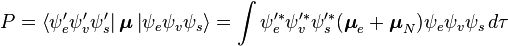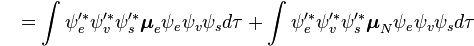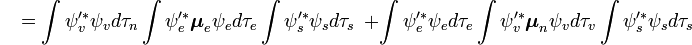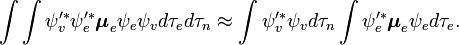Principe Franck-Condon - Définition

Formulation quantique

Considérons une transition dipolaire électrique depuis un état vibrationnel initial (ʋ) de l'état électronique fondamental (ε), , vers un état vibrationnel (ʋ' ) d'un état électronique excité (ε'), (voir notation bra-ket). L'opérateur de dipôle moléculaire μ est déterminé par la charge (-e) et la localisation (r_i) des électrons ainsi que par les charges (+eZ_j) et localisations (R_j) des noyaux :

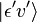
L'amplitude de probabilité P pour la transition entre ces deux états est donnée par :

où et sont, respectivement, les fonctions d'ondes globales des états initial et final. Ces fonctions d'ondes sont le produit des fonctions d'ondes vibrationnelle individuelle (dépendant des coordonnées spatiales du noyau), spatiale électronique et de spin :

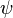
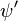
Cette séparation des fonctions d'ondes électroniques et vibrationnelles est une conséquence de l'approximation Born-Oppenheimer et est le postulat fondamental du principe Franck-Condon. En combinant ces équations, on obtient une expression de l'amplitude de probabilité en termes de contributions vibrationnelle, spatiale électronique et de spin :

La partie indépendante du spin de l'intégrale de départ est ici considérée comme un produit de deux intégrales :

La factorisation serait exacte si l'intégrale sur les coordonnées spatiales des électrons n'était pas dépendante des coordonnées nucléaires. Cependant, dans l'approximation Born-Oppenheimer, et dépendent (paramétriquement) des coordonnées nucléaires, et donc l'intégrale (une surface de transition dipolaire) est une fonction des coordonnées nucléaires. La dépendance étant habituellement peu marquée, la négliger (c'est-à-dire le postulat de l'indépendance de la surface de transition dipolaire par rapport aux coordonnées nucléaires, appelée approximation de Condon) est parfois permise.

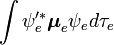
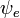
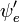
La première intégrale après le signe plus est égale à zéro car les fonctions d'ondes électroniques des différents états sont orthogonales. Il reste donc le produit de trois intégrales. La première est l'intégrale de recouvrement vibrationnel, aussi appelée facteur Franck-Condon. Les deux intégrales restantes contribuant à la probabilité d'amplitude déterminent les lois de sélection électronique spatiales et de spin.

Le principe Franck-Condon étant un postulat sur les transitions vibrationnelles permises entre deux états électroniques différents, d'autres règles de sélection quantiques peuvent diminuer la probabilité d'une transition, voire l'interdire. Les règles de sélection rotationnelles ont été négligées dans la démonstration ci-dessus. Les contributions rotationnelles peuvent être observées dans les spectres de gaz mais sont très fortement atténuées dans les liquides et solides.

Il devrait être clair à ce stade que la formulation quantique du principe Franck-Condon est le résultat d'une série d'approximations, principalement sur la transition électrique dipolaire et la prise en compte de l'approximation Born-Oppenheimer. Les transitions dipolaires magnétiques et électroniques des quadrupolaires électriques plus faibles, avec la validité incomplète de la factorisation de la fonction d'onde totale dans les fonctions d'ondes nucléaires, électroniques spatiales et les spins, impliquent que les lois de sélection, incluant le facteur Franck-Condon, ne sont pas strictement suivies. Pour toute transition donnée, la valeur de P est déterminée par toutes les règles de sélection, bien que la sélection de spin corresponde à la plus grande contribution, suivie par les règles de sélection électroniques. Le facteur Franck-Condon ne module que faiblement l'intensité des transitions, c'est-à-dire qu'il contribue avec un facteur de l'ordre de 1 à l'intensité des bandes dont l'ordre de grandeur est déterminée par d'autres lois de sélection. Le tableau ci-dessous donne l'intervalle des coefficients d'extinction pour les combinaisons possibles de règles de sélection d'orbitales et de spins permis ou non.