Principe de Fermat - Définition
La liste des auteurs de cet article est disponible ici.
Introduction
Le principe de Fermat est un principe physique qui sert de fondement à l'optique géométrique. Il décrit la forme du chemin optique d'un rayon lumineux et s'énonce ainsi :
La lumière se propage d'un point à un autre sur des trajectoires telles que la durée du parcours soit extrémale.
Il permet de retrouver la plupart des résultats de l'optique géométrique, en particulier les lois de la réflexion sur les miroirs, les lois de la réfraction, etc.
Une conséquence première du principe de Fermat est la propagation rectiligne des rayons lumineux dans les milieux homogènes. En effet, dans un milieu homogène, le temps de parcours est proportionnel à la longueur du trajet, et le chemin le plus court pour aller d’un point à un autre est et a toujours été la ligne droite.
Historique
Ce principe doit son nom à Pierre de Fermat, qui l'a énoncé en 1657 mais qui n'a soumis son mémoire, Synthèse pour les réfractions qu'en 1662. Il s'oppose, par cela, à René Descartes, qui dans sa dioptrique, expliquait les lois de l'optique en comparant la lumière à une balle soumise à diverses forces. Fermat se base sur un principe moral :« La nature agit toujours par les voies les plus courtes et les plus simples »
Pierre Louis Moreau de Maupertuis en complète la conception, créant le Principe de moindre action.
Formulation du principe de Fermat à l’aide du chemin optique
Cas d’un milieu homogène
Le chemin optique de la lumière pour aller d'un point A vers un point B dans un milieu homogène, noté L(A,B), est défini comme étant un nombre proportionnel au temps mis par le rayon pour aller de A à B, le coefficient de proportionnalité étant tel que L(A,B) est égal à la distance AB pour un parcours dans le vide. Appelant v la célérité de la lumière dans le milieu, et c celle dans le vide, on a donc
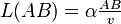
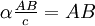
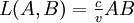
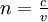
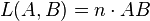
La lumière se propage « plus difficilement » dans les milieux autres que le vide. Exemple : Un rayon lumineux traverse une couche d'eau de 5 cm d'épaisseur. Parallèlement, un autre rayon lumineux traverse 5 cm d'air. L'eau a pour indice de réfraction n = 1,33 et l'air un indice sensiblement égal à celui du vide n = 1. Dans l'eau, le rayon lumineux aura parcouru une distance D = 1,33.5 = 6,65cm. Dans l'air, le rayon aura parcouru une distance D' = 1.5 = 5cm. Le rayon aura parcouru un chemin optique plus long dans l'eau que dans l'air.
Cas d'un milieu continu quelconque
On considère deux points infiniment voisins et distants d'une distance ds. Le chemin optique séparant ces deux points est défini par dL = n.ds ; dL est la différentielle de chemin optique ou encore, l'élément unitaire infinitésimal de chemin optique. Pour trouver le chemin optique L(AB) séparant deux points A et B sur cette courbe, il suffit de faire la somme intégrale de tous les éléments dL sur la coordonnée curviligne s délimitée par les points A et B :
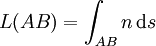
Le principe de Fermat s’énonce alors :
Entre deux points A et B, atteints par la lumière, le chemin optique suivi le long du trajet est stationnaire.
Durées de parcours stationnaires ou minimales
Le principe de Fermat a été énoncé ci-dessus sous sa forme commune mais on doit l'énoncer sous la forme plus rigoureuse :
La lumière se propage d'un point à un autre sur des trajectoires telles que la durée du parcours soit stationnaire.
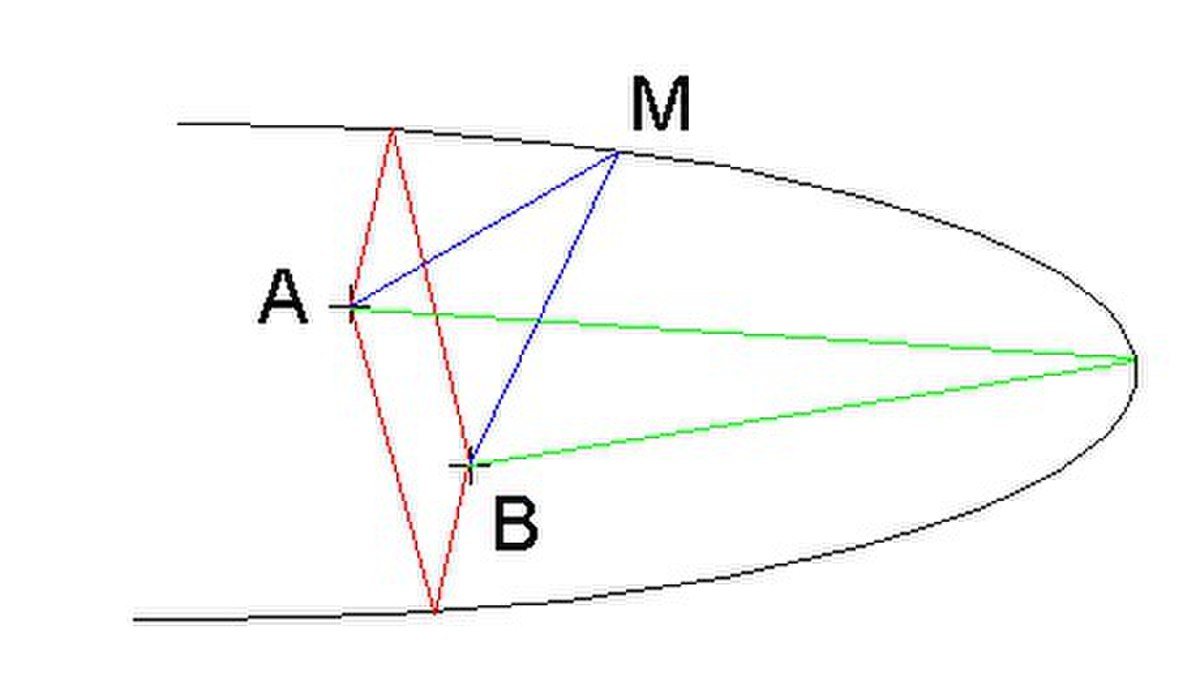
En effet si, dans la plupart des cas, on rencontre des chemins dont la durée de parcours est minimale, il ne faut pas oublier pour autant que d'autres situations peuvent exister. Par exemple, pour aller d'un point A à un point B situés à l'intérieur du miroir concave représenté ci-contre, en se réfléchissant une seule fois sur la surface, la lumière peut emprunter deux parcours de durée minimale (en rouge) et un parcours de durée maximale (en vert) parmi les parcours constitués de deux segments AM et BM. L'étude de la longueur du chemin AMB = AM + MB ferait apparaître trois extrema locaux, deux minima et un maximum, correspondant à ces trajets.
Le terme stationnaire peut être compris à partir de cet exemple. Si le point quelconque M effectue un déplacement infiniment petit du premier ordre à la surface du miroir, la variation du chemin optique est également du premier ordre. En revanche, si l'on considère les trois zones qui correspondent aux extrema, alors un déplacement du premier ordre du point entraîne une variation du chemin optique du second ordre ou plus faible encore. En d'autres termes, lorsque le point M se déplace sur le miroir, la variation du chemin optique est rapide presque partout mais très lente au voisinage des trois points particuliers où elle devient quasi nulle, d'où l'emploi du mot « stationnaire ».
Toutefois, si deux points sont reliés par un chemin suffisamment court, ce chemin minimise la durée par rapport aux autres chemins possibles les plus proches. Pour reprendre l'exemple de la parabole, si les deux points sont sur le trajet vert et sont assez proches de son point de « rebond » sur la parabole, alors pour la longueur du chemin AMB = AM + MB il n'y a plus trois extrema, mais un seul qui est un minima.
Le même problème se retrouve dans l'énoncé du principe de moindre action, qui est à la mécanique ce qu'est le principe de Fermat à l'optique, dans la définition des surfaces minimales (qui ne sont pas forcément... minimales) ou dans celle des géodésiques.

















































