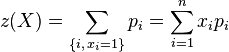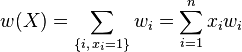Problème du sac à dos - Définition

Énoncé mathématique

Les données du problème peuvent être exprimées en termes mathématiques. Les objets sont numérotés par l'indice i variant de 1 à n. Les nombres w_i et p_i représentent respectivement le poids et la valeur de l'objet numéro i. La capacité du sac sera notée W.

Il existe de multiples façons de remplir le sac à dos. Pour décrire l'une d'elles il faut indiquer pour chaque élément s'il est pris ou non. On peut utiliser un codage binaire : l'état du i-ème élément vaudra x_i = 1 si l'élément est mis dans le sac, ou x_i = 0 s'il est laissé de côté. Une façon de remplir le sac est donc complètement décrite par un vecteur, appelé vecteur contenu, ou simplement contenu : X = (x₁,x₂,...,x_n) ; et le poids associé, ainsi que la valeur associée, à ce remplissage, peuvent alors être exprimés comme fonction du vecteur contenu.

Pour un contenu X donné, la valeur totale contenue dans le sac est naturellement :

De même, la somme des poids des objets choisis est :

Le problème peut alors être reformulé comme la recherche d'un vecteur contenu (les composantes valant 0 ou 1), réalisant le maximum de la fonction valeur totale z(X), sous la contrainte :

(1)

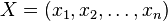
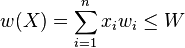
C'est-à-dire que la somme des poids des objets choisis ne dépasse pas la capacité du sac à dos.

En général, on ajoute les contraintes suivantes afin d'éviter les cas singuliers :

•  : on ne peut pas mettre tous les objets ;
•  : tout objet apporte un gain ;
•  : tout objet consomme des ressources.

Terminologie :

• z(X) est appelée fonction objectif ;
• tout vecteur X vérifiant la contrainte (1) est dit réalisable ;
• si la valeur de z(X) est maximale, alors X est dit optimal.

Résolution exacte

Le problème du sac à dos, dans sa version classique, a été étudié en profondeur. Il existe donc de nombreuses méthodes aujourd'hui pour le résoudre. La plupart de ces méthodes correspondent à une version améliorée d'une des méthodes suivantes.

Programmation dynamique

Le problème du sac à dos possède la propriété de sous-structure optimale, c'est-à-dire que l'on peut construire la solution optimale du problème à i variables à partir du problème à i-1 variables. Cette propriété permet d'utiliser une méthode de résolution par programmation dynamique.

On notera KP(i,c) le problème réduit à i variables et à contenance c. L'idée est la suivante :

Étant donné une variable i et une contenance c, les solutions optimales de KP(i,c) sont soit :

• les solutions optimales du problème à i-1 variables avec la même contenance c (KP(i-1,c)), auxquelles on ajoute x_i = 0 ;
• les solutions optimales du problème à i-1 variables avec la contenance c − w_i (KP(i-1,c − w_i)), auxquelles on ajoute x_i = 1.

Le problème du sac à dos à zéro variable (KP(0,*)) a une solution optimale de valeur nulle.

On construit alors une table T[i,c] contenant la valeur des solutions optimales de tout problème KP(i,c) de la manière suivante :

      pour c de 0 à W faire        T[0,c]:= 0      fin pour            pour i de 1 à n faire        pour c de 0 à W faire          si c>=w[i] alors            T[i,c]:= max( T[i-1,c], T[i-1, c-w[i]] + p[i] )          sinon            T[i,c]:= T[i-1,c]          fin si        fin pour      fin pour      

Une fois la table construite, il suffit de démarrer de la case de T[n,W] et de déduire l'état des objets en remontant jusqu'à une case T[0,*].

Cet algorithme a une complexité temporelle et spatiale en O(nW). Cependant, on peut ramener la consommation de mémoire à O(n + W), voire, si seule la valeur de la solution optimale est importante, à O(W). Il a deux avantages :

1. rapidité ;
2. pas besoin de trier les variables.

et un inconvénient :

1. gourmand en mémoire (donc pas de résolution de problèmes de grande taille).

Cette approche nous vient de Garfinkel et Nemhauser (1972).

Procédure de séparation et d'évaluation

Comme tout problème combinatoire, le problème de sac à dos peut être résolu à l'aide d'une procédure de séparation et d'évaluation (PSE). La fonction d'évaluation d'un nœud consiste souvent à résoudre le problème en variables continues (voir plus bas). L'implémentation proposée par Martello et Toth (1990) est devenue une référence. Elle se distingue par :

• une évaluation des nœuds améliorée ;
• une recherche locale lorsque la dernière variable ajoutée au sac a amené à un échec ;
• la nécessité d'un effort intellectuel considérable pour comprendre leur code source.

L'avantage de cette méthode est la faible consommation de mémoire.

Approches hybrides

L'approche hybride n'est pas réellement une nouvelle méthode de résolution. Elle consiste simplement à combiner les deux méthodes précédentes afin d'en tirer tous les avantages. Typiquement, on va appliquer une PSE jusqu'à une profondeur de recherche où le sous-problème sera jugé assez petit pour pouvoir être résolu par programmation dynamique.

Les précurseurs de cette approche sont Plateau et Elkihel (1985), suivis par Martello et Toth (1990). Il y a eu d'autres améliorations depuis.