Produit direct (groupes) - Définition

Exemples

Groupe de Klein

Soit G l'unique groupe d'ordre deux, isomorphe au groupe cyclique d'ordre deux Z/2Z. Sa table est la suivante :

Le groupe produit GxG est un groupe de quatre éléments dont la table est la suivante:

Le groupe obtenu est isomorphe au groupe de Klein, le seul groupe abélien d'ordre quatre, dont tous les éléments ont eux-mêmes pour inverse.

Produit trivial

Soit {e} le groupe réduit à un élément, Gx{e} est un produit de groupe isomorphe à G. On parle alors de produit trivial.

Groupe cyclique

Il est possible de se poser la question inverse, soit G un groupe, par exemple un groupe cyclique d'ordre g, G est-il un produit non trivial de certains de ses sous-groupes. La réponse est donnée par le Théorème des restes chinois.

• G est isomorphe à un produit non trivial de sous-groupes si et seulement s'il existe deux entiers a et b premiers entre eux tel que leur produit soit égal à g.

Dans ce cas, G est isomorphe au produit direct des deux groupes Z/a.Z et Z/b.Z.

Remarque : La démonstration est donnée dans l'article associé.

Groupe abélien

Le cas général ne peut être traité, il est trop vaste, il est donc nécessaire d'apporter des hypothèses supplémentaires. Ces hypothèses correspondent essentiellement à trois cas, traités ici.

Groupe abélien fini

Le cas le plus simple est celui ou le groupe G est fini. Un premier exemple est donné par les groupes cycliques, ils suffisent pour générer, à l'aide du produit direct tous les groupes abéliens finis.

• Il existe une suite d'entiers strictement positifs (a₁,a₂,...,a_k) tel que G est isomorphe au produit direct des groupes cycliques de cardinal les différents éléments de la suite.

Ce qui s'écrit de la manière suivante :

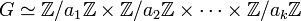
Groupe abélien de type fini

Le deuxième cas est d'une nature proche du cas précédent. Il correspond aux groupes contenant une partie génératrice finie. Il existe ainsi au moins un groupe qui n'est pas élément de l'ensemble précédent, celui des entiers Z. On démontre (dans l'article associé) qu'il est l'unique générateur à ajouter pour obtenir tous les groupes abéliens de type fini.

• Pour tout groupe abélien G de type fini, il existe un entier n et un groupe fini F tel que G est isomorphe au produit direct de F et de Zⁿ.

Groupe de Lie commutatif

Les deux catégories précédentes sont dénombrables. Il existe pourtant des groupes importants qui ne le sont pas, on peut citer par exemple le cas des isométries linéaires du plan utilisé précédemment. Il est alors nécessaire d'adjoindre trois hypothèses : le groupe dispose d'une structure de variété différentielle compatible avec le groupe (on parle de groupe de Lie), l'espace tangent est de dimension finie et le nombre de composantes connexes du groupe est fini. La propriété suivante est alors vérifiée :

• Tout groupe de Lie de dimension finie et ayant un nombre fini de composantes connexes est isomorphe à un produit direct d'un groupe fini, d'un espace vectoriel de dimension finie et d'un tore maximal.