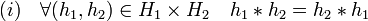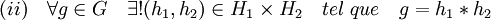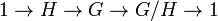Produit direct (groupes) - Définition

Réciproque

La problématique réciproque est la suivante, soit G un groupe, existe-t-il deux sous-groupes H₁ et H₂ de G non triviaux (c’est-à-dire différents de {e} et G) tel que G soit isomorphe au produit direct de H₁ et H₂ ?

La réponse est parfois positive, comme le montre l'exemple des groupes cycliques. Ce n'est pas toujours le cas, le groupe symétrique d'ordre trois, contenant les permutations d'un ensemble de trois éléments, contient six éléments. Les seuls sous-groupes non triviaux ont pour cardinal deux ou trois. Or les seuls groupes de cardinal deux ou trois sont des groupes cycliques donc abéliens. Comme le produit direct de deux groupes abéliens est abélien et que le groupe symétrique d'ordre trois est non commutatif, il n'est pas produit direct non trivial de deux sous-groupes.

Condition nécessaire et suffisante

Soit H₁ et H₂ deux sous-groupes d'un groupe G, les propriétés élémentaires offrent une condition nécessaire pour qu'ils correspondent à un produit direct. Tout élément de G s'écrit comme produit d'un élément de H₁ et d'un élément de H₂ et tout élément de H₁ commute avec tout élément de H₂. Cette condition n'est pas seulement nécessaire, mais aussi suffisante :

• L'application φ de H₁xH₂ dans G qui, à (h₁, h₂) associe h₁*h₂ est un isomorphisme de groupe, si et seulement si :

Le fait que φ soit un morphisme provient directement de la condition (i), en effet :

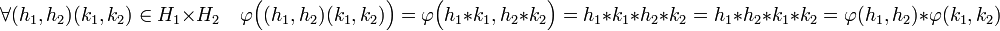
La condition (ii) exprime exactement le fait que φ est bijective. La démonstration est donc achevée.

Somme directe

Soient H₁ et H₂ deux sous-groupes de G. On dit que la somme de H₁ et de H₂ est égale à G si et seulement si le groupe engendré par les éléments de H₁ et de H₂ est égal au groupe entier G et si tout élément de H₁ commute avec tout élément de H₂.

Si, de plus l'intersection de H₁ et de H₂ est réduit à l'élément neutre, alors la somme est dite directe et la notation suivante est utilisée :

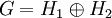
• La somme directe de H₁ et de H₂ est égale à G si et seulement si tout élément de G s'écrit de manière unique comme somme d'un élément de H₁ et d'un élément de H₂.

Cette définition se généralise à n sous-groupes.

La somme directe possède bien des analogies avec son homologue en algèbre linéaire (cf. Somme directe). Soit H₁ et H₂ deux sous-groupes de G, alors :

• La somme directe de H₁ et de H₂ est égale à G, si G est isomorphe au produit direct de H₁ et de H₂.

Projecteur

Une approche, un peu analogue à celle des espaces vectoriel, donne une équivalence entre un produit direct et un morphisme particulier appelé projecteur. Soit G un groupe, H₁ et H₂ deux sous-groupes de G tel que l'application φ du paragraphe précédent soit un isomorphisme. Alors tout élément g de G s'écrit de manière unique h₁*h₂ où h_i est élément de H_i. Soit p l'application de G dans G qui à g associe h₁. Elle bénéficie des propriétés suivantes :

• La fonction p est un morphisme de groupe, tout élément de son image commute avec tout élément de son noyau et pop est égal à p.

Ici o désigne la composition des fonctions.

L'analogie avec les espaces vectoriels donne lieu à la définition suivante :

• Un projecteur p de G est un morphisme de G dans G tel que tout élément de son image commute avec tout élément de son noyau et pop est égal à p.

La donnée d'un projecteur permet une décomposition de G en produit direct :

• Soit p un projecteur de G, alors G est isomorphe au produit direct de l'image de p et du noyau de p.

Dans le cas où G est abélien, tout morphisme dont le carré est égal à lui-même est un projecteur, en effet tout élément du groupe commute avec tout élément du groupe.

Cette propriété peut se reformuler de la manière suivante. Toute suite exacte :

telle que G est abélien, et qu'il existe une section G/H dans G qui se factorise en un produit direct .

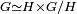
• La fonction p est un morphisme de groupe, tout élément de son image commute avec tout élément de son noyau et pop est égal à p.

En effet, montrons p est un morphisme :

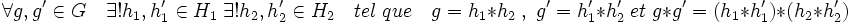
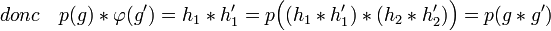
Montrons que pop est égal à p. Soit g = h₁*h₂ un élément quelconque de G, p(g) = h₁. De plus, h₁ s'écrit de manière unique comme produit d'un élément de H₁ et d'un élément de H₂ de la manière suivante h₁=h₁*e, donc p(h₁)=h₁, et la proposition est démontrée.

Montrons que tout élément de l'image de p commute avec tout élément du noyau de p. L'image de p est inclus dans H₁, la proposition précédente montre l'inclusion inverse donc l'image de p est égale à H₁. Montrons alors que le noyau de p est égal à H₂. Par construction de p tout élément du noyau s'écrit e*h₂ avec h₂ élément de H₂ ce qui démontre l'égalité. Le paragraphe précédent montre alors le résultat recherché.

• Soit p un projecteur de G, alors G est isomorphe au produit direct de l'image de p et du noyau de p.

Il suffit de montrer que tout élément de G s'écrit de manière unique comme produit d'un élément h de l'image et d'un élément k du noyau. Soit g un élément de G soit h l'image de g par p et k=g*h^-1. Par construction, h est élément de l'image de p.

De plus, pop(g) = p(g) = p(h) = h, et donc p(h^-1) = h^-1. En conséquence p(k) = p (g)*p(h^-1)=e, et k est bien un élément du noyau. Tout élément de G s'écrit bien comme produit d'un élément de l'image et d'un élément du noyau.

Supposons deux écritures g = h*k et g = i*l d'un élément g de G comme produit d'un élément de l'image et d'un élément du noyau de p. alors i^-1*h = l*k^-1 et le terme de gauche est un élément de l'image et celui de droite du noyau. Comme les deux termes sont égaux, ils appartiennent à l'intersection. En tant qu'élément de l'image, le terme est invariant par p, en tant qu'élément du noyau son image est égal à e, en conséquence i^-1*h = l*k^-1 = e. Ce qui montre l'unicité de l'écriture.